文献标识码: A
DOI:10.16157/j.issn.0258-7998.172119
中文引用格式: 黄伟,黄春跃,翟江辉. 埋入式基板中传输线间串扰问题研究[J].电子技术应用,2018,44(1):13-16.
英文引用格式: Huang Wei,Huang Chunyue,Zhai Jianghui. Crosstalk study on transmission lines of embedded substrate[J]. Application of Electronic Technique,2018,44(1):13-16.
0 引言
随着通讯类电子系统工作频率的不断增加,信号完整性问题变得日益突出,而串扰是影响信号完整性的重要问题之一,任何一对网络之间都存在串扰,串扰超过一定的界限可能引起电路的误触发,导致系统无法正常工作。
埋入式基板技术使电子产品系统具有更高的集成度、灵活性和适应性[1],目前,随着信号频率变高,电路板的尺寸变小,埋入式基板中布线密度加大等因素的影响,串扰问题也越来越不容忽视。
针对传统PCB板中传输线间的信号完整性研究,国内外已有较多文献进行相关报道。在国内,陈建华等人[2]分析了PCB(Printed Circuit Board)内两地层之间的带状线的参数对相邻相同参数的带状线近端耦合噪声和远端耦合噪声的影响;朱兴华等人[3]研究了传输线结构对信号完整性的影响;杨洁等人[4]在多层微波电路中,使用电磁仿真软件HFSS 对过孔进行电磁特性分析,得出过孔散射参数(S参数);在国外,Dries Vande Ginste等人[5]研究了单条埋入式微带线和一对耦合的埋入式微带线的形状参数变化对信号完整性的影响;Yan Dong等人[6]研究了T形微带线之间的串扰;Hyun Ho Park[7]等人利用傅立叶变换法和匹配模型技术对微带线的传输性能和反射做了研究;Monica Zolog等人[8]研究了微带线的几何参数变化对信号完整性的影响;韩德强等人研究了如何利用HyperLynx仿真工具保证板级电路设计的信号质量[9]。上述学者的研究成果一方面表明针对PCB中传输线串扰问题研究的必要性,另一方面也表明针对埋入式基板中传输线间的串扰问题研究较少,尚无针对埋入式基板内相关参数对串扰影响的研究成果。对此,文中在Cadence仿真平台上建立埋入式基板内传输线串扰仿真分析模型,研究包括埋入式基板中布线的宽度和厚度、传输线间的耦合间距和耦合长度以及基板的介电常数在内的结构参数变化对传输线间串扰的影响,找出影响规律并提出抗串扰措施,以达到为进一步提高埋入式基板内传输线抗串扰性能提供理论指导的目的。
1 埋入式基板中传输线仿真模型
1.1 仿真模型
文中串扰仿真在Cadence Allegro 16.6的Sig Xplorer模块下进行,仿真模型如图1所示。攻击网络和受害网络的传输线均为带状线,在仿真过程中,两网络的传输线的参数完全相同。

两传输线的横截面参数如图2所示,用T表示传输线厚度,W表示传输线宽度,S表示耦合间距,D表示基板的介电常数,传输线耦合长度记为L(未在图2中标出),上述5个仿真参数在仿真过程中可以根据仿真需要进行修改。

1.2 仿真参数设置
仿真中设置单层埋入式基板厚度是1 mm,攻击网络信号是占空比为1的50 MHz方波,驱动电压为5 V,输入输出端口模型是标准IBIS输入输出端口。
1.3 仿真结果描述
参考高速PCB中传输线串扰的分析方法[10],仿真结果用被攻击网络的串扰噪声波形进行描述。为比较不同参数对串扰的影响,将不同参数下的串扰波形绘制在同一坐标系下。同时,选取串扰波形中绝对值最大的串扰幅值(串扰峰值)作为量化标准。
2 埋入式基板中传输线的串扰分析
2.1 基板中传输线耦合间距对串扰影响
设置埋入式基板层间厚度为1 mm,W=4 mil,T=18 μm,D=4.5,L=5 mm,设置耦合间距分别为0.5 mm,1 mm,1.5 mm和2 mm,进行仿真,远端串扰仿真波形如图3和图4所示。测量仿真过程中的最大串扰值进行记录,如表1所示。



从图3和图4可以看出,随着传输线耦合间距从0.5 mm增加到2 mm,近端串扰和远端串扰都呈减小趋势,且变化明显,而表1的串扰峰值也反映了同一变化趋势。因此,在埋入式基板的布线过程中,应合理控制传输线间距。
从图3和图4中还可以发现,近端串扰和远端串扰的波形变化与峰值变化趋势一致,因此在后续仿真中仅列出串扰峰值进行量化比较。
2.2 基板中传输线宽度对串扰影响
设置埋入式基板层间厚度为1 mm,T=18 μm,S=1 mm,D=4.5,L=5 mm,参考现行PCB设计标准,设置传输线宽度分别为4 mil,8 mil,10 mil,15 mil,仿真结果如表2所示。

从表2记录的串扰峰值可以看出,随着传输线宽度从4 mil增加到15 mil,近端串扰和远端串扰都逐渐减弱,近端串扰最大值由42.9 mV减小至32 mV,远端串扰最大值由36.8 mV减小至16.5 mV。因此,在进行埋入式基板传输线的设计过程中,要减少串扰,在条件允许的条件下,传输线的宽度应尽量宽些。
2.3 基板中传输线厚度对串扰影响
设置埋入式基板层间厚度为1 mm,W=4 mil,S=1 mm,D=4.5,L=5 mm,设置传输线厚度分别为18 μm,25 μm,35 μm,70 μm进行仿真,结果如表3所示。
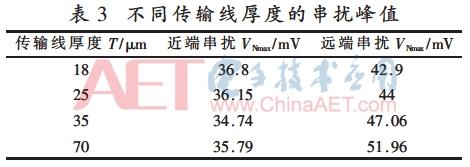
表3记录的串扰峰值数据表明,传输线厚度增加,远端串扰峰值从42.9 mV增至51.96 mV,近端串扰峰值变化不明显,变化范围仅为35±2 mV。因此,埋入式基板设计中,进行传输线的设置时,为降低远端串扰,应尽量减小传输线厚度。
2.4 基板中传输线耦合长度对串扰影响
设置埋入式基板层间厚度为1 mm,W=4 mil,S=1 mm,D=4.5,T=18 μm,设置传输线耦合长度分别为5 mm,6 mm,7 mm,8 mm进行仿真,仿真结果如表4所示。

由表4可以看出,随着传输线耦合长度从5 mm增加到8 mm,近端串扰和远端串扰都呈增加趋势。由此可见,在不考虑其他因素的影响下,传输线耦合长度增加,传输线间的串扰影响会变大。因此,在埋入式基板的布线过程中,应尽量减少两传输线间的耦合长度。
2.5 基板介电常数对串扰影响
设置埋入式基板层间厚度为1 mm, W=4 mil,S=1 mm,T=18 μm,L=5 mm,设置基板的介电常数分别为4.3,4.4,4.5,4.6,仿真结果如表5所示。

由表5可知,基板介电常数增加,近端串扰和远端串扰都有增加的趋势,但增加不明显。因此,在进行埋入式基板的材料选择时,在条件允许的情况下,尽量选择介电常数小的基板。
通过对比表1到表5的近端串扰峰值和远端串扰峰值发现,无论在哪一种情况下,远端串扰峰值均大于近端串扰峰值,所以在进行埋入式基板的设计过程中应重点考虑控制远端串扰。
3 基于正交试验设计的综合分析
3.1 埋入式基板中各参数组合的正交试验设计
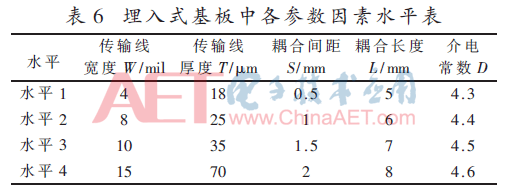
正交设计是多因子试验中最重要的一种设计方法。它是根据因子设计的分式原理,采用由组合理论推导而成的正交表来安排设计实验,并对结果进行统计分析的多因子试验方法[11]。为了综合分析各因素对传输线间串扰的影响,并考虑到PCB的设计规范,根据上一节的单因素分析,设计了五因素四水平L16(45)的正交试验,如表6所示。
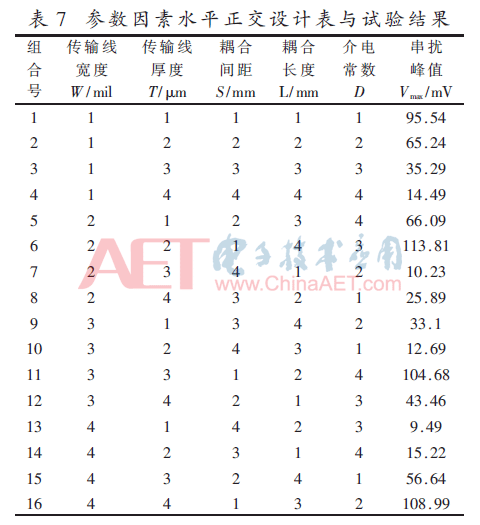
由表7可知,共有16种不同参数水平组合,根据这16种参数组合进行仿真,仿真结果用远端串扰峰值表示,如表7最后一列所示。
3.2 埋入式基板中传输线串扰的极差分析
极差分析方法,就是利用数理统计的方法计算出正交表中每列的极差R值,从而可以得到影响因素的主次顺序。某个因素的极差定义为该因素的最大水平与最小水平之差,极差大表明该因素影响大,是主要因素;极差小说明该因素的影响小,为次要因素[12]。极差分析结果如表8所示。
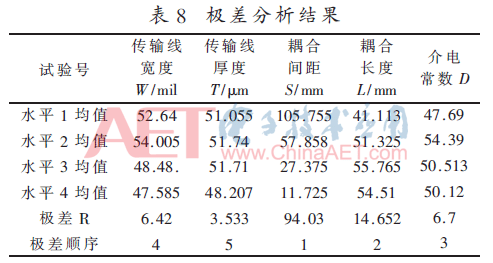
由表8极差的分析结果可知极差的大小顺序为S>L>D>W>T,即影响埋入式基板中传输线间串扰因素的大小排序为:传输线耦合间距影响最大,其次是传输线间耦合长度,再次是基板介电常数,最后是传输线宽度和传输线厚度。由此分析结果可以得出,埋入式基板中的传输线耦合间距和耦合长度对串扰影响较大,因此在进行基于埋入式基板的电路设计时,为保证信号的传输性能,减小串扰,要合理设置两传输线间距,控制两传输线的耦合长度。
3.3 最优组合验证
由表8极差分析结果可知,本次设计中的最优参数水平组合是W4T4S4L1D1,即传输线宽度15 mil,传输线厚度70 μm,传输线间耦合间距2 mm,耦合长度5 mm,介电常数4.3,采用这些最优组合参数,建立相应的仿真分析模型,对最优参数水平组合进行仿真。在最优参数组合下,近端串扰和远端串扰的峰值绝对值均小于10 mV,近端串扰的峰值为3.68 mV,远端串扰峰值为7.03 mV,将该水平下的远端串扰峰值与表7的实验结果比较发现,最优参数组合下的远端串扰峰值最小,由此也进一步验证了正交实验结果的正确性。
4 结论
通过以上分析可知,在埋入式基板中,传输线间的串扰会受到传输线耦合长度、耦合间距、传输线的宽度和厚度以及基板的介电常数所影响,具体结论如下:
(1)在其他条件不变,只改变某一因素的情况下,传输线间的串扰会随着传输线宽度的增加而减小;随着传输线厚度的增加,近端串扰最大值增大,而远端串扰影响不大;传输线间串扰随传输线耦合间距的增加而减小、随传输线耦合距离的增加而增加;随着基板介电常数的增大,最大串扰值略有增加。
(2)极差的分析结果表明:传输线间的耦合间距对埋入式基板中传输线间串扰影响最大,其次是传输线耦合长度,再次是基板介电常数,最后是传输线宽度和传输线厚度;串扰最小的参数组合是W4T4S4L1D1,即传输线宽度15 mil,传输线厚度70 μm,传输线间耦合间距2 mm,耦合长度5 mm,介电常数4.3。
参考文献
[1] 林金堵,吴梅珠.在PCB中埋置有源元件[J].印制电路信息,2010(1):23-31.
[2] 陈建华.PCB传输线信号完整性及电磁兼容特性研究[D].西安:西安电子科技大学,2010.
[3] 朱兴华.印制电路板传输线制作工艺对信号完整性的影响与仿真[D].成都:电子科技大学,2012.
[4] 杨洁.一种微带线-带状线过孔互连结构的电磁特性仿真分析[J].电子技术与软件工程,2015(8):139-141.
[5] Dries Vande Ginste,Daniel De Zutter.Influence of the trapezoidal cross-section of single and coupled inverted embedded microstrip lines on signal integrity[C].2011 30th URSI General Assembly and Scientific Symposium.Piscataway:IEEE Computer Society,2011:1-4.
[6] Yan Dong,Sun Li,Sun Yaxiu,et al.Analysis and suppression of crosstalk for T-shaped microstrip by using FDTD[J].Journal of Electronics and Information Technology,2007,29(9):2283-2286.
[7] Hyun Ho Park.Analysis of microstrip line with bends using fourier transform and mode-matching technique[C].IEICE Transactions on Communications.Tokyo:Maruzen Co.,Ltd.,2010:1731-1738.
[8] Monica Zolog,Dan Pitica.Controlling the signal integrity through the geometry of the microstrip on the digital PCBs[C].Electronics System Integration Technology Conference.Piscataway:IEEE Computer Society,2010:1-6.
[9] 韩德强,谢伟,刘立哲,等.FPGA开发板设计中的信号完整性分析[J].电子技术应用,2011,37(6):28-31.
[10] 刘正青.高速PCB设计中的串扰分析与控制研究[J].湖南工程学院学报(自然科学版),2004,14(4):16-19.
[11] 杨德.试验设计与分析[M].北京:中国农业出版社,2002:171-173.
[12] 何少华,文竹青,娄涛.试验设计与数据处理[M].长沙:国防科技大学出版社,2002:67-68.

