文献标识码: A
DOI:10.16157/j.issn.0258-7998.173601
中文引用格式: 王丹,李孟杰,李玉河,等. 简化的极化码译码算法[J].电子技术应用,2018,44(6):99-102,107.
英文引用格式: Wang Dan,Li Mengjie,Li Yuhe,et al. Simplified polar code decoding algorithm[J]. Application of Electronic Tech-
nique,2018,44(6):99-102,107.
0 引言
2009年ARIKAN E教授提出了极化码[1],并且通过数学方法证明了当码长无限长时其性能可以达到香农极限。极化码一经提出就在国际上引起广泛的关注,并且在2016年11月3GPP RAN1 #87会议上确定5G eMBB场景控制信道编码为极化码。
极化码在实际应用中存在着一些缺点。连续删除(Successive Cancellation,SC)译码对于长码有很好的纠错性能,但是对中短码长译码性能有显著的降低。为了克服这个问题,学者们提出了许多改进方法,如置信传播(Belief Propagation,BP)译码算法[2]、线性规划(Linear Programming,LP)译码算法[3]等。这些算法虽然可以提高一部分译码性能,但是译码算法的复杂度太大。一些算法针对SC算法进行了改进,文献[4]提出了连续删除列表(Successive Cancellation List,SCL)译码算法,特别是在冗余循环校验(Cyclic Redundancy Check,CRC)辅助下的SCL的译码性能可以超过最大似然(Maximum Likelihood,ML)译码[5]。但同时SCL译码的复杂度也随之增加。文献[6]中提出的堆栈SC(SCStack,SCS)译码有和SCL译码相同的译码性能,此外SCS译码的时间复杂度远低于SCL译码,并且在高的信噪比下可以降低搜索宽度L。
本文对SC译码和SCL译码进行了算法简化,降低了算法的复杂度和时延。并且用数学证明的方法证明了简化算法的可行性。
1 极化码编码
Polar Code是一种结构性与迭代性极强的信道编码技术,其设计核心理论是对信道的极化,信道极化过程主要包括两部分[1]:信道联合过程和信道分裂过程。
1.1 信道极化[1]
信道联合:对已知的二进制离散无记忆信道W进行N次迭代复制WN:XN→YN,N=2n,并对复制所得信道进行递推方式组合。WN和WN之间的转移概率关系为:

图1所示为在高斯信道下,码长为N=4 096的信道极化仿真图。根据仿真结果,可以看出部分信道的信道容量成两极分化。据此可以选出I(W)→1的信道传输信息比特作为信息位,I(W)→0的信道传输固定比特作为冻结位。

1.2 极化码编码


2 SC译码算法

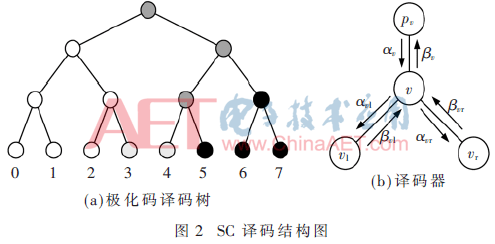


把βv传递给pv。这时v节点的译码消息传递终止,因为在余下译码过程中将不会再次激活节点v。
2.1 简化的SC译码算法
本节通过简化传统译码的消息传递规则,简化了SC译码算法。并且证明简化译码算法的译码性能是与传统的译码性能相同。
(1)Rate-0节点
对于Rate-0节点v,由于它所有后代都是Rate-0节点,因此当v接收到软信息αv时,不去激活左右的子节点而直接计算βv:

对于任意dv=n-1的Rate-1节点一定满足式(15)。假设dv=i的Rate-1节点也满足(15),于是对于dv=i-1的Rate-1节点v的子节点dv=i,满足式(15)。因此,根据上面的推导可以证明式(12)成立。
②证明式(13)成立:当dv=n时,对Rate-1节点,式(13)显然是成立,因此,可以通过归纳法证明dv<n的Rate-1节点也是满足式(13)的。
2.2 算法复杂度分析

3 SCL译码算法
为了提高SC译码算法在码长较短情况下纠错能力,SCL译码算法被提出,L代表搜索宽度。每次必须有一点被估计,它的可能值0和1都需要被考虑。因为存在L组码字候选,所以每次新的位估计产生2L组候选路径,其中一半需要丢弃。因此,路径度量值(Path Metric,PM)被提出。PM计算如下:

SCL译码算法是从根节点出发,按广度优先的方法对路径进行扩展;每一层向下一层扩展时,选择当前层中具有较小PM的L条。当没有到达叶节点而搜索宽度已经达到,按照PM的从大到小的排列保留PM小的L条路径。直到到达叶节点,然后选取PM最小路径作为译码结果。
为了进一步提高极化码的译码性能,编码前在信息比特中添加CRC,然后利用SCL译码算法获得L条搜索路径,最后借助“正确信息比特可以通过CRC校验”的先验信息,对这L条搜索路径进行挑选,从而得到正确译码结果。
4 简化的SCL译码算法
传统的SCL译码算法每次进行路径扩展时都会产生2L条路径,但是对于冻结比特,由于译码结果是已知的,因此对于冻结比特不进行路径扩展,直接判决比特,路径度量值也不改变,从而减少剪枝算法执行的次数,达到降低算法复杂度的目的。


由上述的译码过程分析,式(20)PM的计算可以改为:

因为冻结比特在译码过程中结果是已知的,所以不需要去选择路径,进而PM也不需要计算。另外,由于分裂次数的减少,剪枝算法也随之减少,并最终达到了降低算法复杂度的目的。
5 仿真结果与分析
如图4所示,在高斯信道下,码长为1 024,码率为0.5,采用二进制相移键控调制,译码输出使用24位CRC校验。搜索宽度L分别为1,2,4,8,16,32 的CA-SCL译码性能,仿真数据是106帧,一帧长1 024个比特。仿真结果表明,随着L的值增加,误码率在逐渐降低,CA-SCL译码算法的性能明显要优于SC(L=1)译码算法。

6 结论
极化码是目前唯一可以通过数学证明达到香农极限的信道编码技术,并且已经成为5G控制信道的编码方案。本文详细叙述极化码编译码的原理和结构,并提出关于SC译码和SCL译码的优化算法,在不改变译码性能的前提下,降低了算法复杂度。通过对SC译码和SCL译码的性能进行了仿真分析,结果表明,随着搜索宽度L的增加,极化码的译码性更优,但复杂度也随着增加。因此关于SCL的复杂度和数据吞吐量是下一步研究方向。
参考文献
[1] ARIKAN E.Channel polarization:a method for constructing capacity-achieving codes for symmetric binary-input memoryless channels[M].IEEE Press,2009.
[2] ARIKAN E.A performance comparison of polar codes and Reed-Muller codes[J].Communications Letters IEEE,2008,12(6):447-449.
[3] GOELA N,KORADA S B,GASTPAR M.On LP decoding of polar codes[C].Information Theory Workshop.IEEE,2010:1-5.
[4] TAL I,VARDY A.List decoding of polar codes[J].IEEE Transactions on Information Theory,2012,61(5):2213-2226.
[5] NIU K,CHEN K.Stack decoding of polar codes[J].Electronics Letters,2012,48(12):695-697.
[6] NIU K,CHEN K.CRC-aided decoding of polar codes[J].IEEE Communications Letters,2012,16(10):1668-1671.
[7] BALATSOUKAS-STIMMING A,PARIZI M B,BURG A.LLR-based successive cancellation list decoding of polar codes[J].IEEE Transactions on Signal Processing,2015,63 (19):5165-5179.
作者信息:
王 丹,李孟杰,李玉河,贾东升
(重庆邮电大学 重庆市移动通信技术重点实验室,重庆400065)

