0 引言

    在我国现阶段，飞机精密进近与着陆引导的过程中应用最广泛的保护措施为仪表着陆系统（Instrument Landing System，ILS），该系统能保证在恶劣环境中进行进近和着陆工作的飞行器的安全，但也存在作用距离有限、易受地形遮挡影响等缺点。惯性导航系统（Inertial Navigation System，INS）又存在误差随着时间的增加而慢慢累积这一劣势。而目前国内GBAS着陆系统（GBAS Landing System，GLS）正处在不断完善的过程中，GBAS能提供水平、垂直偏差引导等进近服务，同时还具备Ⅱ、Ⅲ类精密进近、机场场面滑行引导等功能^[1]。

    现有的导航系统出现误差的原因之一，就是由于现实环境中被观测目标的运动具有不确定性，使得传统的非线性滤波算法难以得到较好的滤波精度。而BP神经网络（Back Propagation Neural Network）具有实现任意的从m维输入到n维输出的非线性映射能力^[2]，因此可以利用BP神经网络对传统的滤波算法进行修正，进而提高其滤波精度。

    根据上述的分析，本文提出一种组合导航算法，将INS分别与ILS和GLS相结合，利用其输出位置信息之间的差值作为量测值，使用BP神经网络改进的无迹卡尔曼滤波器（Unscented Kalman Filter，UKF）修正滤波误差，修正后将其补偿到UKF的滤波的估计值上作为新的状态值输出，通过最优加权的方法得到系统的全局最优估计值，从而减小误差，提高进近着陆引导的精度。

1 进近着陆系统误差模型

1.1 ILS

    ILS系统能够在环境条件恶劣的情况下提供正确的进近着陆引导信息^[3]。ILS系统包括3个分系统：下滑信标（Glide Slope，GS）、航向信标（Localizer，LOC）和指点信标（Marker Beacon，MB）。

    ILS辐射场是一个由90 Hz和150 Hz音频信号调制的载波，进场飞机通过比较两个音频信号的调制度差(DDM)得到航向信息及下滑信息。下滑道信息如图1所示。

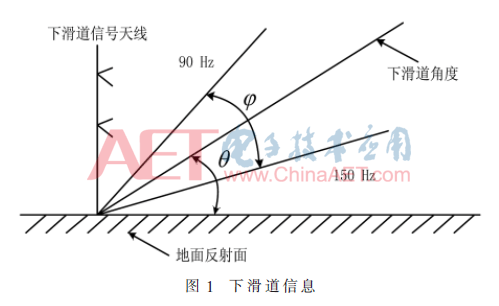
    ILS的系统误差模型如下：

1.2 INS

    INS系统是使用加速度计、陀螺仪等惯性敏感器（Inertial Sensors）来测量载体的线运动和角运动，通过积分来计算载体的运动状态^[4-5]。INS的误差模型如下：

    INS的姿态误差模型为：

    INS的位置误差模型为：

式中：L、λ、h分别为纬、经、高度；v_x、v_y、v_z分别为导航坐标系中的东、北、天向速度。

1.3 GLS

    GLS是一种基于GBAS的进近引导及着陆系统。其优点在于可以实现多跑道覆盖，多类型航空器混合运行，运行效率高、成本低等。GLS在进近过程中通过VHF数据广播电台便可灵活确定飞行器的航路航迹^[6]。

    GLS系统工作时，地面参考接收机的误差(σ_pr-gnd(θ))利用伪距（Pseudo Range，PR）进行校正^[7]。其表达式为：

2 基于BP神经网络的联邦滤波算法

2.1 联邦滤波器

    联邦滤波器（Federated Filter）由1个全局滤波器和n个局部滤波器构成，具有计算量小、容错性好等优点^[8]，各个局部滤波器将各自的最优估计输送到全局滤波器中，在全局滤波器内进行估计信息合成，从而得到全局最优估计^[9]。其结构图如图2所示。

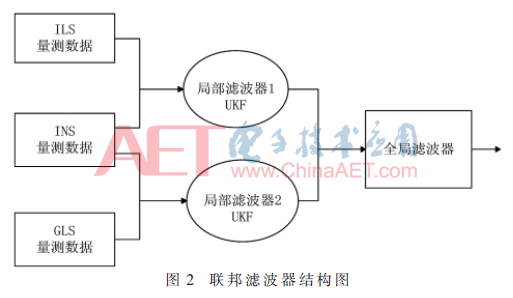
2.2 BP神经网络

    BP神经网络包含1个输入层、n个隐含层、1个输出层三层结构，如图3所示。输入信息通过神经网络的训练，最终达到系统输出信息与期望输出信息尽可能接近的目的。

    BP神经网络的算法如下^[10-11]。假设三层神经网络，则传递函数f(x)为：

2.3 组合系统数学模型

2.3.1 系统状态方程

    由于处于进近着陆阶段，系统可忽略加速度计零偏、陀螺仪角速率偏移的干扰，则INS系统状态变量为：

2.3.2 子系统量测方程

    将ILS/INS组合导航系统、GLS/INS组合导航系统输出位置信息之间的差值^[12-13]作为各自局部滤波器的量测值，则两个局部滤波器的量测方程为：

2.4 分布式局部UKF滤波最优估计

    每个滤波器使用UKF滤波算法更新状态^[14]。

2.4.1 初始状态的统计特性

2.4.2 状态预测估计和状态预测方差

    计算变换后的sigma点： 

2.4.3 预测量测和方差

    利用状态预测值和协方差的结果，按照上一个步骤中确定的采样策略，通过量测函数h(·)计算出变换后的sigma点：  

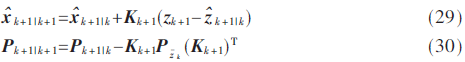
2.4.4 BP神经网络修正

    将式(29)变换为：

    在本文使用的BP神经网络中，网络的最大迭代次数设为500，学习率为0.01，隐含层选取一层，系统训练采用L-M算法^[15]，trainlm型训练函数。

2.5 全局滤波最优估计

3 仿真结果与分析

3.1 数据处理

    本文采用某航空公司的波音737-800型飞机的部分试验数据。在该试验中，飞机由深圳飞往武夷山03号跑道，其下降前的初始高度为6 000 m，初始位置的经纬度为117.990°、27.278°，下滑角为5°。飞机的ILS进近航图如图5所示。

3.2 仿真结果分析

    图6、图7为采用EKF、UKF及基于BP神经网络改进UKF的融合方法所得到的位置误差的均方根误差（Root Mean Square Error，RMSE）曲线，由此可以看出基于BP神经网络改进的UKF的RMSE值比EKF和UKF的都要小，意味着经过BP神经网络改进后UKF滤波算法可以得到更精确的导航精度。

4 结论

    由于在着陆过程中，ILS易受到自身缺陷及外界各种因素的干扰，导致着陆结果存在误差，进而影响飞机着陆时的安全。本文提出一种组合导航算法，将INS分别与ILS和GLS相结合，利用其输出位置信息之间的差值作为量测值，使用BP神经网络改进的UKF修正滤波误差，修正后将其补偿到UKF的滤波的估计值上作为新的状态值输出，通过最优加权的方法得到系统的全局最优估计值，从而减小误差，提高进近着陆引导的精度。

参考文献

[1] 张光明.航空新技术系列报道[N].中国民航报，2012-07-18(004).

[2] 王莉娜，杨剑，孟庆强.消除局域分解端部效应的BP神经网络闭合方法[J].电子技术应用，2017，43(5)：127-130，133.

[3] ICAO，International standards and recommended practices，aeronautical telecommunications，annex 10 to the convention on international civil aviation，volume 1：radio navigation aids[S].Sixth Edition，2006.

[4] PETROVSKA O，SHIKOSKA U R.Aircraft precision landing using integrated GPS/INS system[J].Transport Problems，2013，8：17-25.

[5] Xian Zhiwen，Hu Xiaoping，Lian Junxiang.Robust innovation based adaptive kalman filter for INS/GPS land navigation[C].2013 Chinese Automation Congress.IEEE，2013：374-379.

[6] 陈明强，张光明.GBAS在终端区的应用[J].中国民航飞行学院学报，2011，22（6）：22-25.

[7] SC-159，DO-245A，minimum aviation system performance standards for the local area augmentation system(LAAS)[S].RTCA，2004.

[8] 彭霞，张彦军，崔平远.联邦卡尔曼滤波器与集中式滤波器的等价性[J].青岛科技大学学报，2005，26(2)：169-172.

[9] 钱华明，丁凯雷，艳敏.联邦滤波器及其在船舶组合导航中的应用[J].船舶工程，2007，29（3）：18-21.

[10] 董长虹.Matlab神经网络与应用(第2版)[M].北京：国防工业出版社，2007.

[11] 陈鑫鑫，张复春，郝雁中.神经网络辅助的GPS/INS组合导航滤波算法研究[J].电子技术应用，2015，41(5)：84-87.

[12] 李艳华，房建成，贾志凯.INS/CNS/GPS组合导航系统仿真研究[J].中国惯性技术学报，2002，10(6)：6-11.

[13] 李四海，辛格，付强文.基于INS/ILS/RA组合导航的自动着陆系统[J].中国惯性技术学报，2012，20(3)：311-314.

[14] 万荣荣，李志宇，徐义华.基于卡尔曼滤波的高稳定度测温系统设计[J].电子测量技术，2012，35(4)：29-41.

[15] 王元章，吴春华，周笛青，等.基于BP神经网络的光伏阵列故障诊断研究[J].电力系统保护与控制，2013，41(16)：108-114.

作者信息:

于  耕1，方鸿涛2

（1.沈阳航空航天大学 民用航空学院，辽宁 沈阳110136；2.沈阳航空航天大学 电子信息工程学院，辽宁 沈阳110136）