微处理器的快速发展对电压调节模块VRM(Voltage Regulator Model)的要求越来越高。根据Intel VRD11.1 标准，VRM的输出电压在0.5 V～1.6 V之间，输出电流达到180 A，而且对动态响应和稳态特性提出了严格的要求[1]。在实际应用中，传统VRM多采用多相并联交错同步整流技术来降低电流电压纹波和提高动态性能[2-3]，但并不能降低各并联支路的电感电流纹波。因此，研究者一直致力于将多相电感集成应用到VRM中[4-5]。研究表明，集成磁件在多相并联交错VRM的应用可以使其稳态特性和动态响应都能得到很好地改善，但同时集成磁件之间的磁耦合使得VRM的控制变得复杂。
    最近几年，有学者将精确反馈线性化控制引入到单通道buck变换器和两通道磁集成VRM中，取得了良好的效果[6-8]。参考文献[7]中，将微分几何理论引入到两相磁集成VRM中，在求解两相反馈线性化解耦策略过程中应用了具有二次型性能指标的线性最优控制设计方法。本文以三相磁集成非隔离式VRM为研究对象，将微分几何理论应用到三通道磁集成VRM中，首先建立三输入三输出仿射非线性模型，其次，基于微分几何理论推导出其精确反馈线性化控制规律，实现控制变量的解耦，最后给出了仿真结果。
1 三相磁集成VRM电路模型的建立
    为了建立统一的变换器模型，引入脉冲波形积分法[7]，利用周期脉冲函数将变换器在一个状态周期中的各个子拓扑统一成一个拓扑，假定状态脉冲函数为u1(t)、u2(t)、u3(t)，脉冲函数u(t)取值0和1分别对应实际三相磁集成VRM各相开关管的关断和开通。
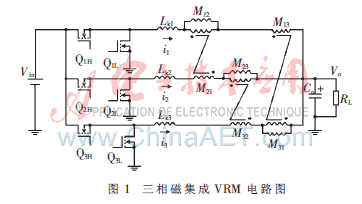
    图1为三相磁集成VRM的电路图，Lk1、Lk2、Lk3为各自通道电感的漏感，M为两两电感之间的互感。三相磁集成VRM工作在电感电流连续模式时，每个开关周期有4个稳定的工作模态。取三相集成电感电流i1、i2、i3和电容电压uo为系统的状态变量，由脉冲函数可得变换器统一模型为：

 
    由式（7）～式（9）、式（12）可以得出三相磁集成VRM的精确反馈线性化控制规律。
4 仿真验证
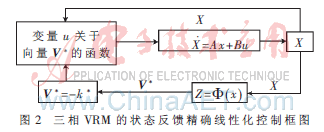
    由上述推导过程得到三相VRM的状态反馈精确线性化控制框图如图2所示。为了验证三相磁集成VRM模型和解耦控制的正确性，本文采用Matlab对基于精确反馈线性化控制的三相磁集成VRM系统进行仿真，同时将仿真结果与输出误差反馈PI控制策略进行了对比。

    本文设计的三相磁集成VRM电路的参数为：输入电压Vin=12 V，输出电压Vo=1.2 V，负载RL=0.02 Ω，每相开关频率f=200 kHz,自感L1=L2=L3取值为0.217 μH，互感M=0.023 5 μH，输出滤波电容C=680μF。
4.1 稳态特性仿真结果
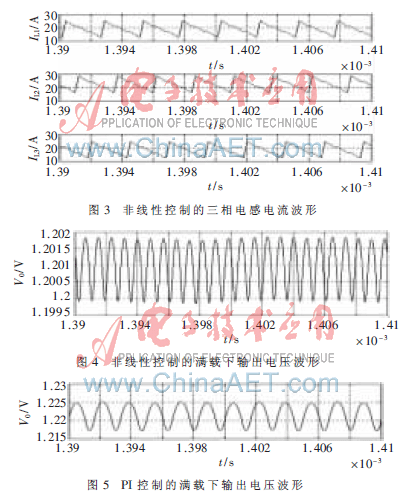
    图3、图4为三相磁集成VRM在精确反馈线性化控制策略下的稳态仿真波形。图3显示了稳态工作时，三相电感电流保持均流；图4中输出电压纹波为1.9 mV，图5中PI控制的输出电压纹波为6 mV，因此可以看出，精确反馈线性化控制能很好地改善系统的稳态特性。

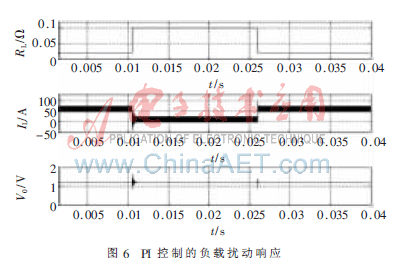
4.2 负载扰动特性仿真结果
    图6是三相磁集成VRM在不同控制策略下的负载扰动仿真波形，设定负载从0.02 Ω跳变到0.1 Ω，然后再回到0.02 Ω。可以看出，非线性控制下电感电流、输出电压波形超调量小，响应时间也更快。

    本文将微分几何非线性控制理论应用到三相磁集成VRM中，实现了三输入三输出精确反馈线性化解耦控制。仿真结果表明，基于微分几何理论非线性控制的三相磁集成VRM具有更好的稳态特性和更高的控制精度，动态响应特性得到明显改善。
参考文献
[1] Intel Corporation.Voltage regulator-down(VRD) 11.1  processor power delivery design guidelines[S].2009.
[2] Yang Qiu. High-frequency modeling and analyses for buck and multiphase buck converters[D].Ph.D Dissertation，Virginia Tech，Blacksburg，VA，November 2005.
[3] 司徒琴，姜建国，佘炎.基于ADP3181的交错并联同步BUCK电路的设计[J].电子技术应用，2007，33(12)：145-151.
[4] Yang Yugang，Yan Dong，LEE F C.A new coupled inductors design in 2-phase interleaving VRM[C].IPEMC，2009.
[5] Yan Dong，Yang Yugang，Xu Ming.Multiphase coupled  inductor voltage regulators(VRs)[C].CPES，2006.
[6] 邓卫华，张波.CCM Buck变换器的状态反馈精确线性化的非线性解耦控制研究[J].中国电机工程学报，2004，24(5)：120-125.
[7] 刘学超，张波.磁集成电压调整模块中磁路耦合的反馈精确线性化解耦控制[J].电工技术学报，2005，20(10)：48-54.
[8] 帅定新，谢运翔，王晓刚.基于状态反馈精确线性化Buck变换器的最优控制[J].中国电机工程学报，28(33)：1-5.
[9] 胡跃明.非线性控制系统理论与应用[M].北京：国防工业出版社，2005.
[10] 洪奕光，程代展.非线性系统的分析与控制[M].北京：科学出版社，2005.