摘  要： 围绕蚁群优化算法的理论及应用，针对蚁群算法在TSP规划中求解能力不足的难题，运用了一种基于自适应的蚂蚁算法，并对TSP规划进行了设计。为了提高路径规划的效率，将自适应与传统的蚂蚁算法相结合形成了自适应蚁群算法。仿真实验结果表明，改进后算法能够在较短时间内找到全局最优路径，相对于基本的蚁群算法在收敛速度、搜索质量和局部寻优方面都有了明显的提高。
关键词： 蚁群算法；自适应；旅行商问题

　旅行商问题[1]（TSP）是数学领域中著名问题之一。假设有一个旅行商人要拜访n个城市，他必须选择所要走的路径。限制条件是每个城市只能拜访一次，而且最后要回到原来出发的城市。路径的选择目标是所有路程之中的最小值。TSP问题是一个组合优化问题，任何能使该问题的求解得以简化的方法，都将受到高度的评价和关注。
　蚁群算法[2]是源于生物世界仿生类随机搜索算法，它应用于组合优化中具有很强的发现解的能力，且具有分布式计算、易于与其他方法相结合及鲁棒性强的优点。在仿真中表现出高度的灵活性、健壮性。但是还存在较多的问题，例如搜索速度慢，局部寻优能力差等。针对这些问题，将算法进行改进，调节信息素Q与信息素挥发系数ρ，使其变为动态的自适应信息素与动态的信息素挥发系数，进行仿真测试改进的优化算法，从而达到更优的结果。
1 基本蚁群算法及其改进
1.1 基本蚁群算法
　蚂蚁在寻找食物过程中总能找到一条食物所在地和蚁穴地之间的最短路程，经研究发现蚂蚁会在其走过的路径上留下称之为信息素的物质，其他蚂蚁可以感知这种物质并以此指引其运动的方向。这种信息素允许叠加，走过同一条路径的蚂蚁数量越多，这条路径上的信息素浓度越大。由此可以吸引其他蚂蚁以更大的概率走此路径。反之，走过的蚂蚁越少，信息素的浓度就越低，行走该路径的概率就越小，同时，这种信息素还会随着时间的推移而挥发[3]。
　设m表示蚂蚁总数量，dij（i，j=0，1，…n-1）表示节点i和节点j之间的距离，τij（t）表示t时刻i、j在连线上的信息素。在算法的初始时刻，将m只蚂蚁随机地放到n个节点上，此时各路径上的信息素相等，设τij（0）为常数，每只蚂蚁根据路径上保留的信息素独立地选择下一个节点。在时刻t，蚂蚁k从节点i转移到节点j的概率为：

　在基本的算法中信息素挥发系数ρ为常数，当处理的问题规模比较大时，由于ρ的存在会使那些从未被搜索到的路径信息素减小到几乎为0，因而降低了算法的全局搜索能力。而当ρ过大时，以前搜索过的路径被再次选择的可能性过大，也会影响算法的随机性和全局搜索能力；反之，通过减小ρ虽然可以提高算法的随机性能和全局搜索能力，但又会使算法的收敛速度降低[1]。因此本文采取自适应改变ρ的值，初始值ρ=1，当最优解在一段时间内无明显改进时，ρ会按式（7）进行自适应调节以加快收敛速度，提高搜索质量。

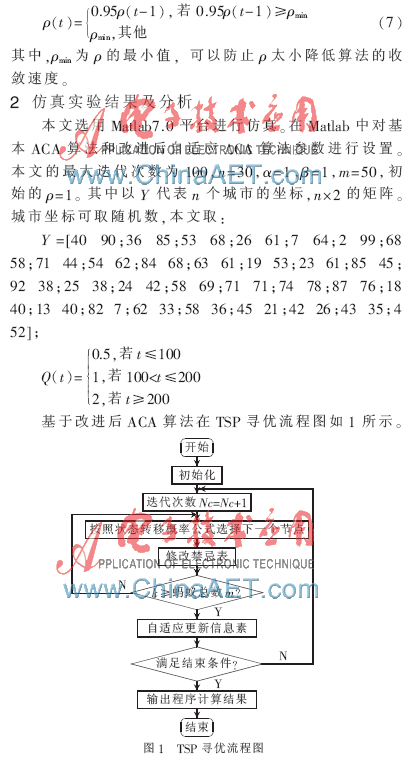
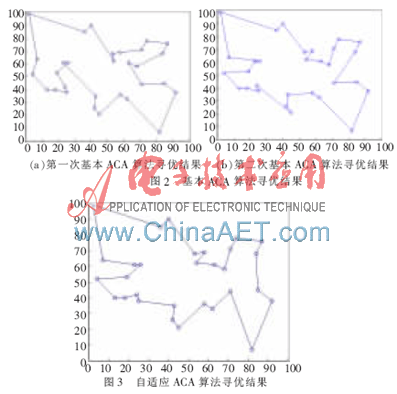
　将基本的ACA算法和改进后的ACA自适应算法同时用于TSP中进行比较分析，通过Matlab绘出的最优解变化图形如图2、图3所示。在Matlab7.0中编程对ACA算法和改进后自适应ACA算法参数进行设置、种群初始化及寻找初始最优值。图2（a）与图2（b）为两次运行基本蚁群算法所得出的最优解，分别为433.623和438.302 2，即所得到的结果稳定性很不好，且每次运行得出的结果相差都较大。图3为改进后算法所得最优路径，仿真中输出为426.465 3。在图中可清晰看到最优值明显比基本算法中有所改进，表明改进后的自适应蚁群算法搜索效率和收敛速度明显提高了。

　本文研究基于蚁群算法的TSP问题，描述了TSP的相关问题和蚁群算法原理。基本的蚁群算法具有较强的鲁棒性，但收敛速度缓慢。针对传统蚁群算法存在搜索时间长、易陷局部最优解，在算法中改进重要的参量——信息素与信息素残留因子，形成动态的自适应信息素，并应用于TSP问题中使运算。论证了将改进后蚁群算法在TSP问题研究应用的可行性，平衡各路径的信息量，使蚂蚁在初始阶段在较大范围内进行搜索，能尽快地找到目标点，并找到最优路径，以避免陷入局部最优。仿真结果表明，相比一般ACA算法，使用改进后的算法可以完成预期的规划效果，在收敛速度、搜索质量和局部寻优方面有了显著的提高。
参考文献
[1] DORIGO M， GAMBARDELLA L M. Ant colonies for the traveling salesman problem[J]. Bio-Systems， 1997， 43（2）：73-81.
[2] DORIGO M， MANIEZZO V， COLORNI A. The ant system： Optimization by a colony of coorperating agents[J].IEEE Transations on System， Man， and Cybernetics-Part B，1996：26（1）：29-41.
[3] 段海滨.蚁群算法原理及其应用[M].北京：科技出版社，2005.
[4] 杨志晓，郭胜国，等．基于改进蚁群算法的机器人路径规划算法[J]．微计算机信息，2008（7-2）：252-253.
[5] 覃刚力，杨家木.自适应调整信息索的蚁群算法[J].信息与控制，2002，31（13）：198-201.
[6] 王颖，谢剑英.一种自适应蚁群算法及其仿真研究[J].系统仿真学报，2002，14（1）：31-33.