摘  要： 针对局部信息识别的重要性，在骨架提取的基础上，提出了一种新的三维模型局部检索方法。该算法在基于骨架树进行图结构匹配的初步筛选后，融入空间结构特征和几何细节特征，进行局部相似度的计算。大量实验证明，本方法对于模型的局部匹配有很好的鲁棒性和高效性。
关键词： 图结构；空间结构特征；几何细节；局部检索

　随着计算机建模和动画技术的发展，三维模型在人类人生活中的地位越来越重要，而对三维模型检索技术的研究也一直是热点之一。相对于模型的整体匹配，局部信息的识别也往往是常用的方法之一。例如，人区分某种动物时，往往通过动物的局部信息就能加以区分（如长颈鹿的脖子、海豚的头部等）。关于三维模型局部算法的研究，目前主要有几下几种：万丽莉等[1]提出了一种基于空间部件分布的方法，该算法是将模型先分割成一系列的部件，然后分别提取子部分的特征，该算法虽然计算速度快，但是依赖于模型分割，且对局部细节特征描述较少。SHILANE P[2]等提了一种基于模型显著几何区域特征对模型进行检索，该算法的核心是对模型表面进行采样，然后根据对4种不同尺度对为半径的球型区域进行分析，得到球面调和描述子，将检索结果用DCG方法评价，最后实现局部匹配。该算法虽然效果较好，但是时间复杂度极高，在实际检索中是不现实的。Spin-image[3]是在模型表面随机采样，然后将每个顶点得到的Spin-image作为局部特征描述符。另外，Chen L B[4]依据Smith-Waterman算法进行局部检索，SHALOM S[5]利用SDF的方法进行局部匹配。鉴于上述方法，本文提出了一种融合空间特征结构的三维模型局部匹配算法，实验证明该方法具有较高的准确率和较好的鲁棒性。
1 算法步骤
　本文算法的流程如图1所示。

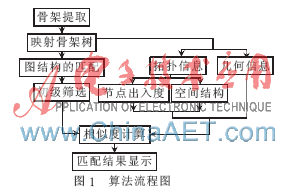
1.1 骨架提取及映射后的骨架树
　传统的Reeb图是一维的图结构，它能够很好地反映模型的拓扑结构，但是却不能很好地描述模型局部细节特征。本文采用参考文献[6]的方法，在MRG算法的基础上改进了基本点的选择和函数的计算，并且通过结合模型表面离散曲率和增加关节特征点的方法，进一步优化了模型的骨架，有效地突出模型的关节特征点，进一步加强了模型检索的准确率。

1.3 空间结构特征的表示与几何信息的计算
　通过对图结构的初级筛选，可以得到几个有着相同或相似结构的子树。由于图结构仅代表着拓扑连接结构，仅靠这种特征并不能准确地得出模型的相似度。比如两个模型的头部拓扑连接图相同，但是在空间中它们的空间结构却很不一样。骨架树是二维的图，而骨架是具有空间结构的三维连接结构，任意两个子节点之间的夹角可以表示模型在空间的结构不同，因此在此基础上融入了空间结构特征。
　在骨架提取的过程中，可以知道各个骨架节点的坐标，以子树部分的父节点作为原点建立空间坐标系，由于知道其子节点在空间中的位置，因此两个子节点之间的夹角很容易得出。在子树部分中，加入子节点之间的夹角特征不仅能够表示其子节点在空间的连接结构，还能够体现子节点与父节点在空间的空间结构。将两个子节点矢量的空间夹角作为模型的空间结构特征：BuildSpatialFeature（）；读取父节点S0与其子节点的空间坐标S1（x1，y1，z1），S2（x2，y2，z2），…，Sn（xn，yn，zn）；利用空间矢量求出父节点与所有子节点构成的矢量（V1，V2，…，Vn）夹角。
　若3点不在一条直线上则：
　getAngleByCoordinate：
　angle（S1）=getAngleByCoordinate（V1V2，V1V3，…，V1Vi）；
　否则：
　angle（S1）=0//所选3个点在同一直线上
　在拓扑连接和空间结构的基础上融入了能够体现局部细节特征的局部突起特征Saliency[7]。对于任意骨架节点都能用式（2）计算出其几何细节特征：
　Saliency=w1Area（Sn）Cure（Sn）3+w2N（Sn）Var（Sn）（2）
　其中，Area（Sn）为骨架节点Sn对应的连通区域的面积与模型总面积的比例；Cure（Sn）是骨架节点Sn对应的连通区域的网格点的标准化之后曲率的平均值；N（Sn）是骨架节点Sn对应的区域曲率极大值或极小值点的个数；Var（Sn）是骨架节点Sn对应的区域曲率的方差；在实验过程中，将w1和w2都赋予0.5。
由于局部细节特征对根节点的影响较小，因此本文由内向外分别赋予各个节点由小到大的权值。这样，每个骨架节点Sn都具有拓扑特征Tf（包括出入度和子节点间的空间的角度）及Gf几何特征（saliency）：Sn（Tf（deg，angle），Gf（saliency）），将其作为特征向量进行相似度匹配。
1.4 局部相似度的计算
　匹配过程中，采用EMD（Earth Mover′s Distance）距离的方法对模型局部进行相似度的计算。EMD算法一般用于对两个分布相似性进行度量，EMD的计算是基于对运输问题的解决，这是一个双边网络流问题，可以表示为以下线性规划问题：假设I为供应商集合，J为消费者集合，Cij为从供应商i∈I对消费者j∈J供给的代价。图4所示是3个供应商和2个消费者的示例[11]。

　本文依据三维模型提取的骨架及骨架点的空间结构特征提出了一种新的三维模型局部检索算法，实验证明该方法能够有效地找到与目标部分相似的子部分，无论是对于不同模型的局部还是同种模型进行变形后的子部分，都能根据本文算法精确地进行检索。
参考文献
[1] Wan L L， Zhao Q P， Hao A M. A method of 3D model retrieval by the spatial distributions of components[J]. Journal of Software， 2007，18（11）：2902-2913.
[2] SHILANE P， FUNKHOUSER T. Selecting distinctive 3D shape descriptors for similarity retrieval[A]. Shape Modeling and Applications[C]. SMI， 2006.
[3] JOHNSON A E， HEBERT M. Using spin images for efficient object recognition in cluttered 3D scenes[J]. IEEE Transactions on pattern analysis and Matchine Intelligence， 1999，21（5）.
[4] CHEN L B， FERIS R S， TURK M. Efficient partial shape matching using Smith-Waterman algorithm[C]. Proceedings of the 2008 IEEE Conference on Computer Vision and Pattern Recognition（CVPR）， Anchorage， AK， USA， 2008：1-6.
[5] SHALOM S， SHAMIR L S A， et al. Part analogies in sets of objects[A]. Eurographics Workshop on 3D Object Retrieval， 2008.
[6] 韩丽，楚秉智.关节特征约束的3维模型骨架提取算法[J].中国图象图形学报，2011，16（4）：660-665.
[7] GAL R， COHEN-OR D. Salient geometric features for partial shape matching and similarity[J].ACM Trans.Graph.， 2006，25（1）：130-150.
[8] 张晓东.三维模型的形状特征提取方法研究[D].青岛：中国石油大学（华东），2010.
[9] HILAGA M， SHINAGAWA Y， KOMURA T， et al. Topology  matching for fully automatic similarity estimation of 3D shapes[C]. Computer Graphics Proceedings Annual Conference Series， ACM SIG- GRAPH Los Angeles， California， 2001：203-212.
[10] 韩丽，张黎娜，楚秉智.一种MRG骨架树的三维模型检索算法[J].计算机工程与应用，2011，47（31）：167-170.
[11] RUBNER Y， TOMASI C， GUIBAS L J. A metric for distributions with applications to image databases[C].Proceedings of the 1998 IEEE International Conference on Computer Vision，1998.