稀疏阵列由于其能以较少的阵列单元数构造高方向性天线阵，可以简化大规模天线阵的馈电网络复杂度以及成本低等原因达到了较广泛的应用，但同时阵列变稀也会出现非常高的旁瓣。稀疏阵列优化的主要目的是实现峰值旁瓣电平(PSL)的最优化。近年来，随着计算机技术的飞速发展，高效的稀疏阵列优化方法已成为研究热点。用于稀疏阵列优化的算法主要有遗传算法[1]、模拟退火算法、分区动态规划法、粒子群算法[2]以及最近出现的蚁群算法[3]等，这些算法从本质上来说都是基于随机性的自然算法，往往需要很长的运算时间才能得到优化结果。
　　本文介绍了一种基于迭代FFT算法的矩形稀疏阵列的优化方法。这是一种全新高效的优化方法。与基于其他算法的优化方法相比，该方法在得到显著优化效果的同时，却只需要少得多的运算时间。本文对参考文献[4]中的算法步骤进行分析和改进，得出了运用迭代FFT算法进行矩形稀疏阵列优化的详细步骤，并对该优化方法的性能进行了分析。
1 矩形阵列模型
    考察由图1所示的xy平面上M行N列个阵列单元构成的矩形平面阵列，各阵元激励幅度和相位相同，dx和dy分别表示沿x和y轴方向阵元间距，设第(m,n)个单元的复激励值Amn，其二维阵列天线方向图可描述为：


    (8) 将归一化的阵元激励Amn再进行二维IFFT变换得到阵列的方向图，求出峰值旁瓣电平PSL，把它与迭代前的PSL进行比较。如果优于迭代前的PSL，则记下该PSL以及阵列的分布位置，如果比迭代前的PSL更差，则不做任何操作。
    (9) 重复步骤(3)~步骤(8)，直到PSL达到给定的旁瓣约束条件，或迭代次数达到给定的一次循环迭代允许的最大迭代次数。
    (10) 步骤(2)~步骤(9)为一次迭代循环步骤。根据给定的迭代循环总次数，进行Num次迭代循环，就完成了整个优化流程。
    实验表明，一次迭代循环往往经过2~5次迭代便会得到最优的PSL，一般每一次迭代循环得到的最优PSL（局部最优PSL）未必能达到给定的旁瓣约束条件，但是制定合理的旁瓣约束条件，就能使局部最优PSL接近给定的旁瓣约束。因此只要独立地进行足够多次迭代循环，每次迭代循环都以一个随机的初始阵元激励数组开始，就有很大的概率得到一个最优或近似最优的阵元分布。由于在MATLAB中有现成的一维FFT和二维FFT函数，为FFT的计算带来了极大的方便，所以运用FFT算法计算线阵和平面阵列的方向图函数，加快了整个优化过程的完成。
3 仿真结果
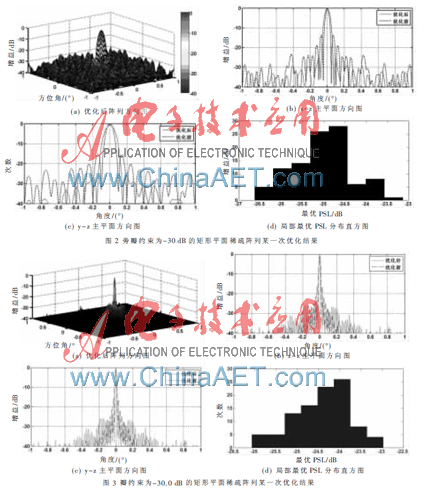
   下面对迭代FFT算法进行仿真验证，分别给出了不同孔径、不同稀疏率情况下的优化结果。仿真参数为：阵元均为全向性天线单元，xy平面上栅格间距dx=dy=0.5 λ,逆FFT与FFT运算点数K×K=256×256, 迭代循环总次数Num=100次。图2~图3中的(a)图为与最优PSL相对应的阵列方向图，(b)图为x-z主平面方向图，(c)图为y-z主平面方向图， (d)图为每次大循环后得到的最优PSL分布直方图。

3.1 矩形平面阵列优化结果

    阵列大小为20×40，稀疏率为62%，旁瓣约束为－30 dB的矩形平面稀疏阵列某一次优化结果如图2所示，在x-z和y-z两个主平面得到的最优PSL分别为－25.51 dB和-26.01 dB。与参考文献[6]中对相同阵列大小、相同稀疏率的矩形平面稀疏阵列运用免疫算法进行优化，得到的最优PSL为-24.05 dB和-24.78相比较，分别改善了1.46 dB和1.23 dB，并且通过图2(d)可以看出迭代循环得到的最优PSL，有80%都是小于-24.5 dB的。
    阵列大小为100×100，稀疏率为70%，旁瓣约束为-30.0 dB的矩形平面稀疏阵列优化结果如图3所示，在x-z和y-z两个主平面得到的最优PSL分别为-24.12 dB和-24.86 dB。目前没有相关文献对如此大规模的矩形平面阵列做过稀疏优化，通过图3(d)可以看出迭代循环得到的最优PSL，有85%都是小于-23.5 dB的。
3.2 基于迭代FFT算法的优化方法的性能分析
    以上所有仿真均在Matlab 7.9中完成，计算机配置为：Intel Pentium(R) Dual-Core CPU E5500处理器，主频为2.8 GHz，内存2 GB，每次仿真所花费的时间仅需1 min左右。在相同计算机配置的情况下，对阵列大小为20×40，稀疏率为62%的矩形平面稀疏阵列，运用交叉率为0.6，变异率为0.01，终止代数为150代的遗传算法进行优化，需要的仿真时间为20 h左右。运用迭代FFT算法可以对任意阵元均匀间隔的平面阵列进行稀疏优化，在达到显著优化效果的同时，与基于其他算法的优化方法相比，却只需要少得多的时间，由此证明了该优化方法的快速性和有效性。但是迭代FFT算法也有其运用的局限性，它可以用于栅格等间距的线阵和平面阵列的稀疏优化，对于复杂的旋转面共形阵列天线的优化还是要运用遗传算法，模拟退火算法以及粒子群等优化方法。
 
    通过分析表1和表2的数据，可以发现每次优化得到的最优PSL总是在一个小的范围内变化，这证明了该优化方法的有效性和稳健性。
    本文首次使用迭代FFT算法实现了矩形平面稀疏阵列的优化设计。该方法适用于按矩形或三角形排列的任意形状平面阵列天线的稀疏优化。仿真结果证明了该方法的快速性、有效性和稳健性，对解决此类问题提供了有益的启示，为工程运用提供了有价值的参考。
参考文献
[1] HAUPT R L. Thinned arrays using genetic algorithms[J]. IEEE Trans. Antennas Propagation,1994,42(7):993-999.
[2] JIN N, SAMII Y R. Advances in particle swarm optimization for antenna designs: Real-number, binary, single-objective and multi-objective implementations. IEEE Trans. Antennas Propagation, 2007,55(3):556-567.
[3] TERUEL Q O, IGLESIAS E R. Ant colony optimization in thinned array synthesis with minimum sidelobe level[J].IEEE Antennas and Wireless Propagation Letters, 2006,5(1):349-352.
[4] KEIZER W P M N.Large planar array thinning using iterative FFT techniques. IEEE Trans[J]. Antennas Propag. 2009,57(10):3359-3362.
[5] 李建新，陈瑞.基于FFT平面相控阵天线方向图快速计算[J].微波学报，2009,25(6):12-17.
[6] 张建华，王玉峰，庞伟正.矩形平面稀布旁瓣电平的免疫算法优化[J].系统工程与电子技术,2009,31(4):711-744.