摘  要: 以图像与图像平移的并集作为状态集,以探针与探针拷贝的并集作为输入字母表,用向量加减法构造状态转换映射和输出映射,给出了实现数学形态学基本运算开运算的有限自动机。与通用计算机对图像的串行处理相比，开运算自动机采取了并行结构。开运算自动机将运算的时间复杂度降低到了探针像素个数减1。
关键词: 图像处理；分形；形态学开运算；有限自动机

     虽然通用计算机已被广泛地应用于图像处理，但是就其体系结构而言是不适合处理图像数据的。通用计算机的串行性限制了它在图像处理中的效率，因此有必要开发专用的图像处理器。自20世纪60年代MATHERON G和 SERRA J创立了用于图像处理的数学形态学以来，在过去的50多年里得到了大量基于数学形态学的图像处理器,包括Golay逻辑处理器[1]、Diff3[2]、PICAP[3]、Leitz 纹理分析系统[4]、CLIP 阵列处理器[5]、细胞计算机[6]和Delft 图像处理器[7]。这些处理器对于图像的局部变换有较好的效果,它们都属于原胞机器[8]。
    自20世纪90年代KARI J将自动机应用于图像压缩以来，在过去的近20年里，得到了基于有限自动机的大量图像压缩的有效算法[9]，并且将其中一些算法转化成了实际的图像压缩技术[10]。
    数学形态学和自动机理论之所以能够被应用于数字图像处理，是因为多数图像具有分形性。而数学形态学中的探针体现了这种分形结构[11]，有限自动机识别的正规语言的正规分解也体现了分形结构[12-13]。
     本文将有限自动机应用于数学形态学基本运算开运算的实现，得到了可对图像进行并行处理的有限自动机，降低了开运算的时间复杂度。

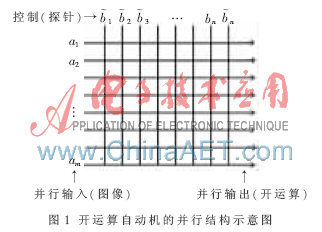
    设图像A含有m个像素点，探针B含有n个像素点。关于开运算的算法复杂度有如下结论。在通用计算机上，完成开运算需要串行地进行2m×n次加减法和m×n次查找,而在开自动机上完成仅需要并行地进行2n-1次加减法和n-1次查找。因此，利用有限自动机实现图像开运算，其时间复杂度仅取决于探针的像素个数n，而与图像的像素个数m无关。由于在图像处理中探针通常要比图像小得多，因此用有限自动机实现开运算对降低运算的时间复杂度是有效的。
    用开运算的有限自动机可以降低运算的时间复杂度。然而，开运算结果的优劣取决于探针的选择，并将直接影响到数字图像处理的效果，只有探针选择恰当，开运算才有价值。因此,利用有限自动机实现探针选取是一项有意义的工作。
参考文献
[1] GOLAY M J E. Hexagonal parallel pattern transformations[J]. IEEE Transactions on Computers, 1969,18(8):733-740.
[2] GRAHAM M D, NORGREN P E, The Diff3 analyzer: a  parallel/serial Golay image processor[C]. Real Time Medical Image Processing, 1980:163-182.
[3] KRUSE B. Design and implementation of a picture processor [D]. Linkoeping: University of Linkoeping, 1977.
[4] KLEIN J C, SERRA J. The texture analyzer [J]. Journal of Microscopy, 1977(95):349-356.
[5] DUFF M J B. Parallel processors for digital image processing [C]. Proceedings of the International Symposium, Bad Neuenahr, 1979:265-279.
[6] LOUGHEED R M, MCCUBBREY D L. The cytocomputer: a practical pipelined image processor[C]. Proceedings of IEEE Annual Symposium on Computer Architecture,France,1980:271-278.
[7] GERRITSEN F A, AARDEMA L G. Design and use of DIP-1: a fast flexible and dynamically microprogrammable  image processor[J]. Pattern Recognition, 1981,14(6):319-330.
[8] NACHTEGAEL M, SUSSNER P, MELANGE T. On the role of complete lattices in mathematical morphology: from tool to uncertainty model[J].Information Sciences,2011(181):1971-1988.
[9] KARI J. Image processing using finite automata[J]. Studies  in Computational Intelligence, 2006(25):171-208.
[10] TISCHIER G.Theory and applications of parametric weighted finite automata[D]. Wurzburg: University of Wurzburg, 2008.
[11] DROSTE M, KUICH J, VOGLER H. Handbook of weigted automata[M]. Berlin: Springer-Verlag, 2009.
[12] LIU Y J.Regular component decomposition of regular languages[J]. Theoretical Computer Science, 2003,299:734-749.
[13] LIU Y J, XU Z B. Semigroup method in combinatorics on words[J]. Chinese Journal of Computer,2005,28: 1138-1145.