文献标识码: A
DOI:10.16157/j.issn.0258-7998.166774
中文引用格式: 陆川,杨超,陈新. 一种认知智能电网中频谱接入策略选择机制[J].电子技术应用,2017,43(9):114-118.
英文引用格式: Lu Chuan,Yang Chao,Chen Xin. A spectrum access strategy selection scheme for the cognitive radio based smart grid network[J].Application of Electronic Technique,2017,43(9):114-118.
0 引言
随着物联网技术的快速发展,需要通信的电力终端数量急剧增长,频谱资源短缺开始出现,并日益严重。为此,认知无线电技术被引入到智能电网的无线通信网络,构建认知智能电网(Cognitive radio based Smart Grid network,CR-based SG)。其通过动态频谱接入技术,为SG节点补充可用频谱资源[1-3]。在CR-based SG中,SG内的节点和网关被称为是次用户,TV频段用户被称为主用户[4]。现有的CR-based SG文献往往只考虑了CR网络的不确定性,具体包括感知误差、对主用户的干扰等[2-3]。至今,如何将CR网络的可用频谱资源的不确定性和SG网络内节点通信环境的不确定性联合进行考虑,并以此为基础设计相应的SG无线通信网络,依旧是一个实际存在的问题。
SG节点中通信环境的不确定性表示节点的通信负载随着时间而变化。一般的,单个节点的通信负载包括:控制信息、系统监测信息和电表读数[5-6]。随着无线多媒体传感网络的大规模普及和成本降低,在智能电网中,对电力消费终端和清洁能源的发电端实施实时监测逐渐普及。前者主要集中在对电力消耗终端的使用状况进行监测,确保电网的高效和稳定;后者指对清洁能源设备的监测,以对其实时发电量进行有效地预测,保障SG能量调度系统的平稳运行。基于此,当SG节点的电力负载增大时,意味着较多家用电器被开启,SG系统内的监测数据量大幅增加,SG节点的通信负载也大幅增大。此外,住宅区部分家用电器在半夜会被关闭,由于监测信号的缘故,需要传输的总数据量下降,节点通信负载下降。然而,此时部分TV频段可能会关闭,出现空闲的频谱资源。为此,对于CR-based SG节点来说,传输通信负载与可用频谱资源之间存在折衷问题。
基于上述分析,本文首先构建一种适合于CR-based SG网络的分析模型,并提出一种频谱接入策略优化选择机制。SG节点可用根据自身的传输需求和其所处环境的实时可用频谱资源状况,在每个时隙开始时优化选择不同的频谱接入策略(即:Underlay,混合接入),以最大化节点的有效传输覆盖范围。最后,本文给出了相应的仿真分析案例,以验证所提优化策略的有效性。
1 系统模型
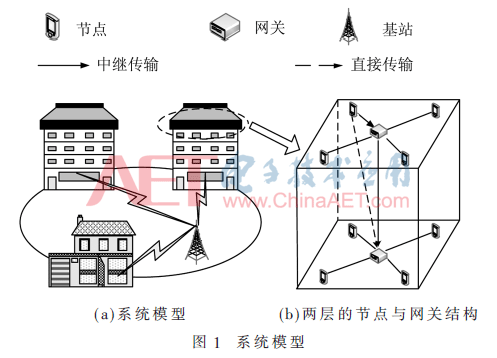
CR-based SG系统模型如图1所示。节点代表的是家庭内智能电表,通过无线通信技术与网关相连,如图1(a)所示。SG内节点的数据传输路由策略并不是本文重点,采用一种常规的聚集树形拓扑结构[7],设定为路由策略。每层均设有一个网关,且网关与节点之间是通过Underlay接入策略相连,以保证链路的畅通。在Underlay接入策略下,无论节点与网关之间的信道是否被占据,节点均可以将数据有效地传输到网关。基于此,数据路由策略设计为:每一个SG节点将其传输的数据发送给与同一层的网关,通过一跳的链接链路。然后,网关由上到下通过多跳的数据传输,最终由最底层的网关将数据发送到户外的基站。
两层的SG节点和网关结构如图1(b)所示。图中,按照其所处的位置不同,网关分为中继网关和下一层网关。中继网关指在Underlay接入策略下就存在的网关,无论其与节点间信道被占据与否,该网关与其同一层SG节点之间链路畅通。下一层网关指布置在紧接着中继网关的下一层的网关。假定单个SG节点不能直接传输数据到两层之外的网关,其传输范围只能覆盖下一层。对于SG节点来说,根据其传输范围,存在两种传输数据模式:直接传输和中继传输模式。直接传输指SG节点直接将数据传输到下一层网关。与之相对应,中继传输指的是SG节点将数据传输给中继网关,再由中继网关将接收到的数据转发给下一层网关。
SG节点(如:次用户)以时隙的形式与主用户共享频谱资源。在不同的时隙,次用户节点的电力负载、通信负载和可用频谱资源存在差异。假定CLn(i)与PLn(i)为次用户n在时隙i的通信和电力负载,n∈[1,2,…,N],i∈[1,2,…,I]。CLn(i)会随着PLn(i)的增大而增大。当节点的电力负载增大时,这意味着住宅内家用电器被开启。然而,当所有家用电器都被开启时,PLn(i)≥PL2,节点的通信负载达到最大值,CLn(i)=CLmax。反之,当节点的电力负载低于某预定值时,PLn(i)≤PL1,此时,CLn(i)=CLmin。在其余常规时隙内,假定PLn(i)与CLn(i)服从独立均匀分布,节点的通信负载CLn(i)可以表示为:

式中,PL1与PL2表示电力负载的门限值,CLmax与CLmin为通信负载的门限值。
对于CR网络,假定当SG节点的电力负载较大时,PLn(i)≥PL2,CLn(i)=CLmax,主用户信道的空闲概率较低,即Pn,i(H0)≤Pth(H0),Pn,i(H0)为信道n在时隙i的空闲概率,Pth(H0)为空闲概率的门限值。在其余时隙,信道空闲概率满足独立随机均匀分布。在本文,频谱资源分配问题不讨论,每一个用户可以分配一条信道,n也表示次用户所占据的主用户信道编号。
2 频谱接入策略优化选择
为了确保网络覆盖,网关的布置是以网络状况最差情况布置的,Underlay接入策略成为选择。然而,节点的通信负载和可用频谱资源是时变的。SG节点可优化选择频谱接入策略,以获得较大的数据传输速率。基于此,作者将对SG节点的频谱接入策略选择进行分析,以平衡节点通信负载与可用频谱资源之间的矛盾。
当PLn(i)≥PL2,CLn(i)=CLmax时,SG节点的通信负载达到最大值,主用户信道空闲概率为Pn,i(H0)≤Pth(H0)。此时,Pn,i(H0)已足够小,次用户不对信道进行感知即可获得更大的平均传输速率。为此,次用户可以直接选Underlay接入策略[3],选择中继传输模式。P1n(i)表示为次用户在n时隙i的发射功率。为了保护主用户的通信受到的干扰低于预定值,P1n(i)严格受限,P1n(i)≤P1,P1表示在Underlay接入策略下的发射功率门限值。
当信道空闲概率增加时,Pn,i(H0)>Pth(H0),若是其选择对信道进行感知,次用户可以获得较大平均传输速率。若此时节点的通信负载下降,频谱资源的供应与需求均发生了变化。为此,混合接入策略成为节点传输策略的最佳选择。SG节点选择对直接传输信道进行感知。根据不同的感知结果、信道占据与否的实际状况以及节点的实时传输需求,节点可用选择两类传输模式:直接传输与中继传输模式。在混合接入策略下,节点n在时隙i的传输结构如图2所示。节点n首先对直接传输信道进行探测。平均传输速率Rdn(i)为:
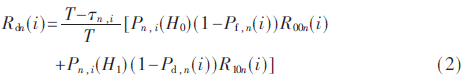
式中,T表示时隙的时长,τn,i表示感知时间长度,Pd,n(i)和Pf,n(i)分别表示感知的判决概率和虚警概率。本文选择能量检测方法进行频谱感知[8]。

当感知结果为信道占据时,节点n需要返回到中继传输模式,如图2(b)所示。使用半双工中继转发方法,仅一半时隙被节点用于传输数据,中继传输信道的平均传输速率Rr n(i)为:
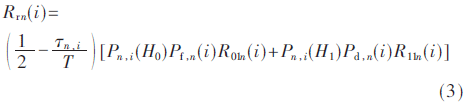
式中,R00n(i)、R01n(i)、R10n(i)、R11n(i)分别表示在不同的感知结果和信道实际占据状况下的信道传输速率[3]。P2n(i)表示感知结果为空闲时,次用户的发射功率,P2n(i)≤P2。
在时隙i开始时,节点n需要判断是否对直接传输信道感知。为此,需要计算直接传输信道的最大平均传输速率。然而感知会消耗时间,当结果为占据时,需要返回中继传输模式。为了满足覆盖需求,Rdn(i)和Rrn(i)均需大于通信负载,即无论是选择何种模式,其平均传输速率均应该大于通信负载。分析发现,直接传输信道的平均传输速率Rdn(i)与信道的感知时间τn,i,发射功率P2n(i)和空闲概率Pn,i(H0)有关。因此,需要对τn,i和P2n(i)进行联合优化,以最大化Rdn(i),同时,保证对主用户的干扰低于预定值,满足SG节点的传输需求。该优化问题P1为:
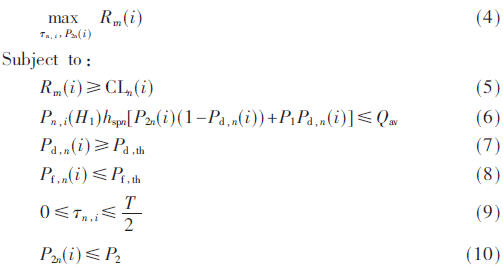
式中,Pd,th与Pf,th分别表示判决概率和虚警概率的门限值。式(5)表示当感知结果为占据时,节点退回到中继传输模式,中继传输的平均信道速率大于节点的传输通信负载,以保证通信网络覆盖。式(6)表示节点n对主用户的平均干扰值低于预定值Qav,hspn表示节点n与主用户接收端之间的信道增益。为了确保感知准确性,一般而言Pd,th=0.9,Pf,th=0.1[4]。

至此,优化问题P1变成一个变量为感知时间的单变量优化问题,并且自变量的取值范围在封闭区间。为此,采用一维穷举方法得到最优感知时间τn,i,并得到Rdn(i)的最大值,记为Rdn,max(i)。当Rdn,max(i)≥CLn(i),需要对直接传输信道进行感知。当感知结果为空闲时,次用户选择直接传输模式。反之,节点返回中继传输模式,以确保网关覆盖完整。
基于上述分析,节点n在时隙的频谱接入策略优化选择机制,总结如算法1所示。次用户可以根据不同的信道状况和通信负载,选择合适的频谱接入策略。
算法1:频谱接入策略优化选择机制:
输入:信道空闲概率Pn,i(H0),通信负载CLn(i),门限值PL1和PL2,
(1) If Pn,i(H0)≤Pth(H0),then
(2) SG节点选择Underlay接入策略,优化传输功率。节点选择中继传输模式;
(3) Elseif Rdn,max(i)≥CLn(i),then
(4) SG节点选择混合接入模式,并感知直接传输信道进行感知;
(5) If 感知结果为空闲,then
(6) SG节点选择直接传输模式;
(7) Else
(8) SG节点选择中继传输模式;
(9) End
(10) End
(11) SG返回到中继传输模式;
(12) 输出:SG选择合适的频谱接入策略,并选择合适的传输模式。
3 仿真分析
本节将对所提出的优化问题P1,以及相对应的频谱接入优化选择机制(简称:优化选择机制)进行仿真分析。作为比较的机制分别是:中继传输和直接传输机制。在中继传输机制中,所有的SG节点均选择Underlay接入策略;在直接传输机制中,所有节点均选择Overlay接入策略,对直接传输信道进行感知,当感知结果为空闲时接入信道,当感知结果为占据时,则传输出现中断。为了验证算法的有效性,本文选择楼宇环境对所提策略进行仿真分析。网关和节点的坐标选择是在一个小范围内随机选取的。楼层的面积为20×20 m2,分为4个均匀的区域,在每一个区域安放一个SG节点。网关从中心区域半径为2 m随机选取。假定所有楼层SG节点和网关的布置都是一样的。由于其存在随机变量,随机选取位置,本文采用蒙特卡洛方法进行仿真,随机独立进行200次仿真,加和取平均值,若没特别说明,主要仿真参数如表1所示。
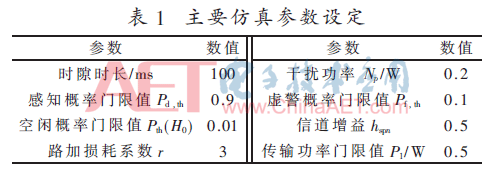
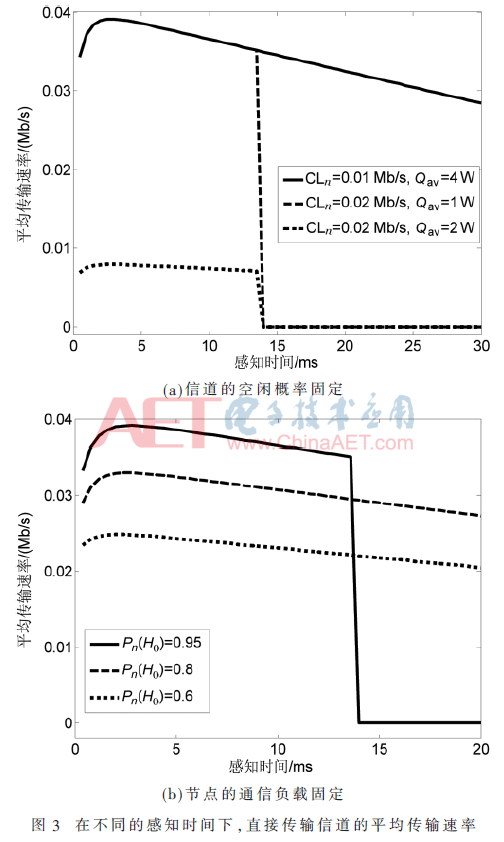
图3表示在单个时隙内不同感知时间下,直接传输信道的平均传输速率Rdn的变化情况。因为是在单个时隙内分析问题,可将时隙标号i隐去,在两种状况下对Rdn进行分析。在图3(a)中,节点的通信负载和干扰门限值不同,信道空闲概率为Pn(H0)=0.95。由图可知,当Qav=4 W和Qav=2 W两类状况下,当τn<14 ms时,上述两类状况下平均传输速率是一样的。这是因为在上述情况下,节点的发射功率均等于P2。当τn≥14 ms,CLn=0.02 Mb/s时,传输速率为0。其原因在于当感知时间增大时,可用的传输时间减小,中继传输信道的平均速率下降,已不能满足节点通信负载需求,传输出现中断。图3(b)分析在不同Pn(H0)时直接传输信道的平均传输速率,节点的通信负载和干扰门限值设定为一样的。CLn=0.02 Mb/s,Qav=4 W。由图可知,当感知时间较小时,传输速率相对于感知时间是一个凸函数,这是因为感知时间的大小会直接影响到感知效果:Pd,n和Pf,n。当Pn(H0)=0.95,τn≥14 ms时,Rdn减小为0,这是因为当感知时间增大时,剩余的传输时间不足,导致中继传输信道平均速率Rrn小于通信负载,信道发生中断。
与图3分析单个时隙内节点的信道平均传输速率不同,在图4中将对多个时隙的节点信道平均传输速率进行分析。假定时隙时长是30 min,在不同的时隙,其直接传输信道的空闲概率不同。在时隙21~24,Pn,i(H0)=0.01,在其余时隙,Pn,i(H0)满足均匀独立分布,区间是[0.01,1]。由图4可见,相比于其余两种机制,所提出的优化选择机制下,节点可以获得更多的传输速率,且不会发生信道传输中断。在优化选择机制中,节点可得到的平均传输速率为Rdn+Rrn,节点在Underlay和Overlay接入策略之间切换。在中继传输机制中,节点可得到的平均传输速率为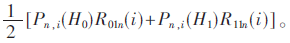 在直接传输机制中,节点的平均传输速率为Rdn,显然,当感知结果为占据时,节点传输会发生中断。继续分析可以发现,大部分时候(例如:时隙1~时隙20,时隙25~时隙30),优化选择机制所获得信道平均传输速率是最好的。然而,在时隙21~25之间,优化选择机制的性能与中继传输一样。这是因为当信道空闲概率太小时,本文所提选择机制可以直接切换到Underlay接入策略,以保证系统不出现中断。然而,在直接传输机制中会出现中断,严重影响系统性能。
在直接传输机制中,节点的平均传输速率为Rdn,显然,当感知结果为占据时,节点传输会发生中断。继续分析可以发现,大部分时候(例如:时隙1~时隙20,时隙25~时隙30),优化选择机制所获得信道平均传输速率是最好的。然而,在时隙21~25之间,优化选择机制的性能与中继传输一样。这是因为当信道空闲概率太小时,本文所提选择机制可以直接切换到Underlay接入策略,以保证系统不出现中断。然而,在直接传输机制中会出现中断,严重影响系统性能。

4 总结
在CR-based NAN智能电网通信网络中,SG节点的电力负载、通信负载和主用户信道的空闲概率是实时变化的,与人们的生活和所处地息息相关。为此,为了平衡节点的通信负载与可用频谱资源之间的矛盾,本文提出了一类节点的频谱接入策略优化选择机制,SG节点根据不同的负载情况和实时的信道状况,选择合适的频谱接入策略,并选择合适的传输模式。数值仿真结果验证了所提策略的有效性。
参考文献
[1] ZHANG Y,YU R,NEKOVEE M,et al.Cognitive machine-to-machine communications:Visions and potentials for the smartgrid[J].IEEE Network,2012,26(3):6-13.
[2] DENG R,CHEN J,CAO X,et al.Sensing-performance tradeoff in cognitive radio enabled smart grid[J].IEEE Transactions on Smart Grid,2013,4(1):302-310.
[3] YU R,ZHANG C,ZHANG X,et al.Hybrid spectrum access in cognitive radio based smart grid communications systems[J].IEEE Systems Journal,2014,8(2):577-587.
[4] STEVENSON C,CHOUINARD G,LEI Z,et al.IEEE 802.22:The first cognitive radio wireless regional area network standard[J].IEEE Communications Magazine,2009,47(1):131-139.
[5] WANG H,QIAN Y,SHARIF H.Multimedia communications over cognitive radio networks for smart grid applications[J].IEEE Wireless Communications,2013,20(4):125-132.
[6] HUANG J,WANG H,QIAN Y,et al.Priority-based traffic scheduling and utility optimization for cognitive radio communication infrastructure-based smart grid[J].IEEE Transactions on Smart Grid,2013,4(1):78-86.
[7] AL-ANBAGI I,EROL-KANTARCI M,MOUFTACH H.Delay-aware medium access schemes for WSN-based partial discharge measurement[J].IEEE Transactions on Instrumentation and Measurement,2012,63(12):3045-3057.
[8] LIANG Y,ZENG Y,PEH E,et al.Sensing-throughput tradeoff for cognitive radio networks[J].IEEE Transactions on Wireless Communications,2008,7(3):1326-1337.
作者信息:
陆 川,杨 超,陈 新
(广东工业大学 自动化学院,广东 广州510006)

