0 引言

    电动空调是一种完全由电能驱动的空调装置，大规模应用于电动汽车领域。电动空调将压缩机、电机、电控合并在一起，代替传统的独立式控制及散热方式，通过利用部分冷媒对系统进行冷却，这种方式相较于传统风冷方式散热效率更高，并且使得空调的体积减小了40%，质量减轻了70%^[1]。

    电动空调的产热量主要来自电源部分、压缩机、电机以及其他生热部分，其中电源部分产生的热量最多。电动空调在额定功率下工作时电源部分产生的热量占总产热量的52%^[2]，这部分热量主要由功率模块产生，因此对电动空调功率模块的散热研究就尤为重要。

    由于功率管的损耗受结温影响较大，且导通电流和集射极电压与结温并不成线性关系，目前很难通过计算得到准确的损耗值^[3]，因此对于电动空调功率模块的散热设计只能通过经验进行，造成散热精度不高。本文提出了一种基于空间插值算法计算损耗的策略，在此基础上建立了热量从功率模块传导至冷媒的数学模型，为散热设计做好了基础。

1 基于三维插值算法的功率模块损耗计算

    功率模块发热主要是由IGBT和二极管的通态损耗及开关损耗引起的^[4]，在实际工况中，流过IGBT和二极管的电流始终处于变化状态^[5]，因此需要计算IGBT和二极管的瞬态通态损耗及开关损耗。

    电动空调功率模块总共有6个桥臂，若每个桥臂有个IGBT芯片并联，则功率模块在一个完整周期内总损耗为：

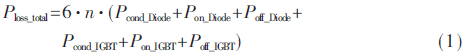
    利用式(1)计算IGBT损耗时最大的难点是，结温对集射极电压和导通电流都有影响，而集射极电压和导通电流又反过来影响结温，器件手册一般只给出了结温在25 ℃和125 ℃时的阈值电压、导通电流、开关电流等参数，只能计算相关温度下的损耗，而对于要想计算任意结温时的损耗就显得无能为力了。对此本文提出了基于三维插值算法的功率模块损耗计算模型。

    以IGBT的开通损耗计算为例，P_{on_IGBT}是关于集射极电压U、电流I、结温T_vj的函数，可以表示为：

    A1~A6均满足式(2)所示的关系，利用实验可以测得这6个点的所有电压、电流、结温以及损耗值。利用三维空间插值算法可以用O点某个邻域范围内的数值逼近O点的实际值。计算过程如式(3)所示：

    同理，可以计算出IGBT的关断损耗、导通损耗、二极管的开关损耗及其导通损耗，进而计算出功率模块总的损耗P_{loss_total}。

2 功率模块散热分析

    电动空调在运行过程中处于相对密闭的环境当中，几乎不受太阳辐射及其他辐射影响，其热量传递的主要形式是固体间的热传导以及对流换热。

    图2是冷媒散热的结构示意图，功率管产生的热量先通过热传导的方式将热量依次传递给绝缘垫、基座、导热硅脂、散热片，最后经过对流换热的方式由冷媒将热量带走^[6]。

    功率管在刚开始工作时，功率管与基座散热片的温度差值较小，随着功率管工作时间的延长，功率管温度的上升，与基座和散热片的温度差值越来越大，此时通过热传导和热对流交换的热量越来越多，最终冷媒带走的热量与功率管产生的热量形成一种动态平衡，功率管温度将不再上升。

    分别列写各层热量传导方程以及对流换热方程，如式(4)所示：

    在选定功率模块后，R_thjc将固定不变，热量传导面积A也不变，因此要改变总热阻，只能通过减小外部热阻来实现，通过分析式(8)可以得出减小外部热阻的两条有效途径：(1)提高各层导热系数；(2)减小各层厚度。

3 仿真分析

    功率管与基座之间垫有一层0.5 mm厚的绝缘导热垫，下层的散热片上开有小孔，供冷媒流过。由于两块固体相紧密接触时难免会留有缝隙，而静止状态下，空气的热传导系数只有0.023 W/m·K^[7]，因此需要在散热片与基座之间涂一层0.2 mm厚的导热硅脂。导热硅脂的作用是将两块固体结合缝隙中的空气排挤出去，减小无效的导热接触面积^[8]。

    采用有限元软件进行热分析时，需要设定各部分材料的特性参数，与热特性相关的参数主要包括热导率和比热容，功率模块各部分材料特性参数具体数值参照国标设定，其仿真结果如表1所示。

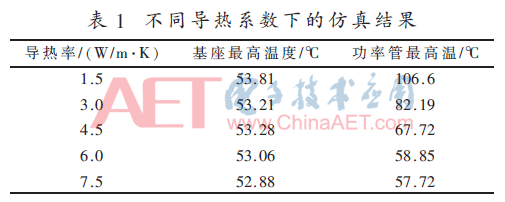
    可以看出随着导热率的增加，基座表面温度基本维持在53 ℃左右。功率管温度则从106.60 ℃大幅降低至57.72 ℃。

    当导热率为1.5 W/m·K时，功率管的最高温度与基座表面最高温度相差将近53 ℃，这主要是因为绝缘垫的存在，其热阻较大，热量难以及时地传给散热板。

    当导热率为7.5 W/m·K时，基座与功率管之间的温度差已减小至不足5 ℃。此时功率管散发的热量能够及时地传导至散热片，由冷媒带走，不会造成热量累积。

    绝缘垫和导热硅脂的厚度只有0.2 mm，不具有大幅减小的空间，所以仅对基座的厚度进行削减。仿真结果如表2所示。

    从表中可以看出随着基座厚度的减小，基座表面最高温度及功率管最高温度也都逐渐减小，这与从理论中得出的散热壁厚度越小，热阻越小，导热性能越好的结论相符。

4 实验结果验证与分析

    为了保证热量不散失到周围空气中，实验中采用保温隔热泡沫制作出一个紧凑密闭的空间。分别将3根pt100铂热电阻探头粘结在功率管1、功率管2及基座中央上，在泡沫板上钻出小孔，供pt100引线引出用，小孔与引线之间的缝隙采用密封胶密封，功率管引线也必须从小孔中引出并严格密封好。

    为了验证不同导热率条件下功率模块的散热情况，依次选用导热率为1.5 W/m·K、3.0 W/m·K、4.5 W/m·K、6.0 W/m·K、7.5 W/m·K的导热垫作为功率管与基座之间的导热材料，利用数据采集卡将测得的温度数据显示并记录下来，并绘制成曲线图，如图3、图4所示。

    可以看出，随着导热系数的增加，功率管温度大幅降低，基座温度基本保持不变，不同导热系数情况下，实验结果与仿真结果走势基本一致，且实测值与仿真值之间的误差均在5%以内。当导热系数分别为1.5 W/m·K、3.0 W/m·K时，基座最终温度远小于功率管温度，当导热系数为7.5 W/m·K时，基座最终温度与功率管最终温度较为接近。这是由于当导热垫导热系数为7.5 W/m·K时，热量传导非常通畅，功率管与基座之间热阻非常小。在导热系数为1.5 W/m·K、3.0 W/m·K时，实测温度略小于仿真温度，这是因为一部分热量通过热辐射的形式散失到周围泡沫材料和空气当中。

    为了验证基座壳体厚度对散热性能的影响，需保证其他参数保持不变。当采用导热率为3.0 W/m·K的导热垫时，不同基座壳体厚度时实测数据与仿真数据对比曲线如图5、图6所示。

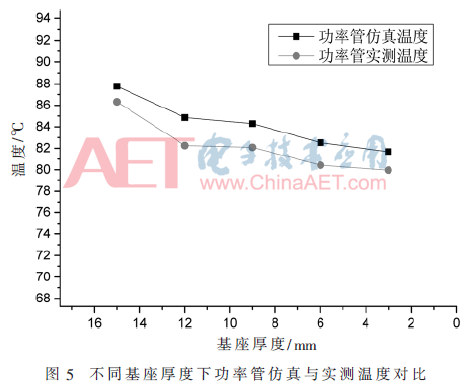
    对比仿真结果与实测结果可以看出，随着基座厚度的减小功率管温度和基座温度均呈现出减小的趋势，说明基座厚度的变化对功率管和基座温度均会产生影响。还可以看出随着基座厚度的减小，功率管和基座温度下降的幅度越来越小，最后趋于稳定。这主要是由于基座厚度的减小虽然可以减小热阻，但是减小到一次程度时，功率管发热量与系统传热量形成平衡，再降低热阻已无助于更多热量传导。对比图4和图6可知，通过减小基座厚度的方法功率管温度减小的幅度不如通过提高导热系数的方法大。

5 结论

    本文提出了一种基于空间插值算法计算出功率模块损耗的方法，利用已知邻域内若干点位处的参数值及其损耗值来逼近未知点位处的损耗值。并通过建立热量从功率模块传导至冷媒的数学模型，提出了降低热阻的两种途径：(1)增加绝缘垫导热系数；(2)减小基座厚度。采用有限元分析软件分别对不同导热系数和不同基座厚度时的系统结构进行了热仿真，并搭建实验平台，验证了理论分析的正确性以及仿真结果的准确性。

参考文献

[1] 张狄林.IGBT电气参数的温度特性分析[J].计算机与数字工程，2013，41(6)：999-1001.

[2] 曹中义.电动汽车电动空调系统分析研究[D].武汉：武汉理工大学，2008.

[3] JANICKI M，NAPIERALSKI A.Modelling electronic circuit radiation cooling using analytical thermal model[J].Microelectronics Journal，2000，31(9)：781-785.

[4] 殷炯，翁星方，何为国，等.IGBT功率模块散热系统设计与分析[J].机电信息，2014(15)：146-148.

[5] 孙潇.用于芯片散热的蒸发冷却技术[D].上海：东华大学，2011.

[6] Wang Shuwang，Zhao Weijian，Tang Zhiguo.Thermal analysis of water cooled electric machine’s controller for electric vehicle[J].Journal of Tongji University(natural science)，2013，41(19)：11-13.

[7] 周飞，赵成勇，徐延明.考虑热学特性的高压IGBT模块暂态模型[J].高电压技术，2016，42(7)：2215-2223.

[8] 李岩磊，杨宁，马颖涛.IGBT结温的近似计算方法及应用[J].铁道机车车辆，2015，35(2)：36-40.

作者信息：

陆  地1，薛敬伟1，梁嘉宁2

(1.西安建筑科技大学 机电工程学院，陕西 西安710055；2.中国科学院深圳先进技术研究院，深圳 广东518055)