文献标识码: A
DOI:10.16157/j.issn.0258-7998.182278
中文引用格式: 高强,李易隆,李大华,等. 基于EEMD-SE和GARBF的短期电力负荷预测[J].电子技术应用,2019,45(1):51-54,59.
英文引用格式: Gao Qiang,Li Yilong,Li Dahua,et al. Short-term power load forecasting based on EEMD-SE and RBF optimized by genetic algorithm[J]. Application of Electronic Technique,2019,45(1):51-54,59.
0 引言
短期电力负荷预测是电力系统运行和调度的关键问题,它是电力系统经济运行的前提,有效的电力负荷预测不仅对电网规划,而且对其安全稳定经济运行有着重要的影响[1]。
电力负荷预测作为一项基础性研究,长期以来一直受到人们的重视。许多专家学者对预测理论和方法做了大量的研究,并提出了若干预测模型和方法。目前,负荷预测的方法有很多,主要可分为两类:一类是统计类的经典预测方法,如回归分析、时间序列方法、灰色预测方法等;另一类是人工智能预测方法,例如专家系统和人工神经网络。随着人工智能的发展,人工神经网络被广泛地应用在预测方面[2]。目前学者大多用的是BP神经网络进行负荷预测,是因为其有着比较强的泛化能力以及非线性映射的能力,但是在使用过程中会发现它很容易陷入局部最小,而且收敛的速度比较慢,所以限制了BP神经网络的发展。与BP神经网络相比,逐渐发展的RBF神经网络避免了BP网络的不足,被广泛应用在短期电力负荷预测方面[3]。
本文提出的EEMD-SE-GARBF神经网络组合的预测模型主要是通过EEMD算法自适应地对负荷序列进行分解,接着结合样本熵对复杂度相似的子序列进行合并,这样有效减小了运算的规模。然后,基于每个子序列的复杂度的差异,构建相应的RBF神经网络模型,并通过遗传算法优化网络参数,避免了神经网络陷入局部最优和收敛性问题。最后把每个新子序列的预测结果相加,得到最终预测值。
1 EMD和EEMD的原理
1.1 EMD分解法
经验模态分解(Empirical Mode Decomposition,EMD)[4]广泛应用在处理非平稳信号方面,自适应地分解出频率各不相同的本征模态函数(Intristic Model Function,IMF)分量,并且每个IMF分量要符合如下条件:信号过零点的个数与信号极大值点、极小值的和相等,即便不相等也不能超过一个;信号局部最小值、最大值的包络均值为零。
(1)设x(t)为原始信号,找到其最大值点和最小值点,然后用3次样条曲线方法将其连成曲线,得到信号x(t)的上下包络线,计算两条包络线的均值m1(t),进而求出信号x(t)与均值m1(t)的差值h1(t):

1.2 EEMD分解法
在使用EMD方法时,如果信号中有噪声或信号中有中断现象,这样就会产生模态混叠。集合经验模式分解(Ensemble Empirical Mode Decomposition,EEMD)是一种基于EMD的改进方法[5-6],它将高斯白噪声添加到原始信号中,然后对信号多次EMD算法处理,可以有效降低模态混叠程度。


2 样本熵
样本熵(Sample Entropy,SE)是Richman提出的时间序列复杂性测试方法[7]。其避免了近似熵的不足,使近似熵误差有所降低。可参考文献[7]了解样本熵主要算法。
样本熵的估计值为:

式中,Bm(t)为任一个时间序列与模板匹配的概率,m代表维数,r代表阈值,N代表长度。SampEn的值与m和r有关,一般情况下m=1或2,r=0.1SD~0.25SD(SD表示原始信号xi的标准差),本文m=2,r=0.2SD。
3 遗传RBF神经网络建模
3.1 RBF神经网络模型
径向基函数(Radical Basis Function,RBF)神经网络[8]具有非线性映射能力较强、网络结构简单、容错性强、鲁棒性强等特点,它可以有效地解决非线性问题,因此被广泛应用在函数逼近、模式识别、时间序列分析和图形处理等领域。
RBF的网络结构如图1所示。它是一种3层前馈型网络,输入层到隐含层的函数变换是线性的,而隐含层到输出层的函数变换是非线性的。其中,隐含层采用的是径向基函数[9]。
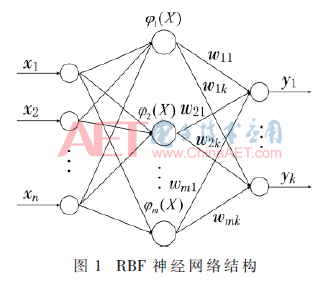
RBF神经网络的非线性传递函数采用高斯径向基函数,其隐含层的传递函数表示为:
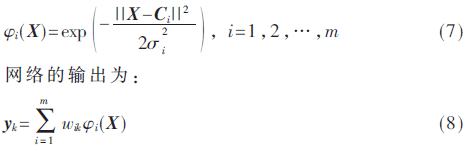
其中,X∈Rn为n维输入矢量,即X=[x1,x2,…,xn];Ci表示第i个基函数的中心;σi为第i个非线性变换单元的宽度;||·||通常取欧氏范数,即||X-Ci||=[(X-Ci)T(X-Ci)]1/2;m为隐含层单元个数;wik为连接隐含层与输出层的权值。
3.2 RBF神经网络模型改进
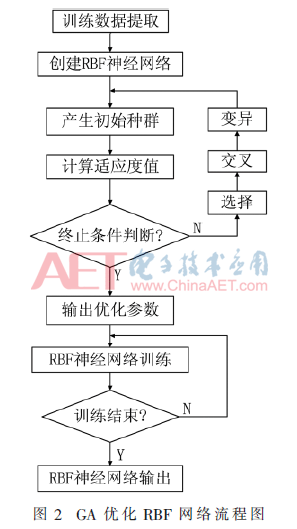
遗传算法(Genetic Algorithm,GA)是一种寻优方法,其与神经网络组合用来训练网络以及优化学习规则。由于神经网络权重阈值是随机初始化的,因而容易产生局部最优,遗传算法的全局收敛性不仅可以解决神经网络结构选择的不确定性问题,而且可以提高网络收敛性能。
利用遗传算法对网络的3个参数(中心矢量Ci、基宽σi和网络连接权值wik)进行全局寻优,保证网络的各参数在全局最优范围内。将式(9)作为个体的适应度函数。

4 基于EMD-SE-GARBF神经网络的预测模型
4.1 模型设计
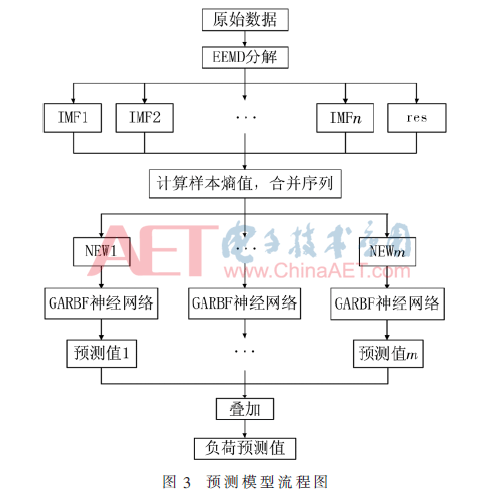
结合几种方法的优点建立短期电力负荷预测模型,模型流程如图3所示,具体预测流程如下:
(1)对输入数据预处理,由于输入变量的单位和取值范围均不相同,因此利用式(10)对数据归一化处理,取值范围设置在[0,1]。

式中,x表示归一化变量,x′表示归一化后的变量,xmax和xmin分别表示变量的最大值和最小值。
本文定义工作日为“1”,休息日为“0”。并对预测日天气进行量化处理,结果如表1所示。

(2)利用EEMD方法对负荷时间序列进行分解,得到各个IMF分量和一个剩余分量。
(3)计算各个子序列的样本熵值,将熵值接近的子序列合并成新子序列。
(4)对每个新子序列建立GARBF预测模型。
(5)利用GA算法对RBF神经网络模型进行参数寻优,最后得到各新子序列的预测值。
(6)叠加每个新子序列的预测值以获得最终预测值。
4.2 仿真分析
为了验证本文提出的短期负荷预测模型EEMD-SE-GARBF的有效性,使用某大学活动中心的数据,对2018年7月6日24小时用电负荷进行预测,训练样本为预测日前23天的原始数据。历史负荷数据如图4所示。

利用EEMD对历史负荷序列进行分解,分解结果如图5所示。可以看出有6个复杂度不同的IMF分量和1个变化比较平缓的剩余分量,计算这7个序列的熵值,结果如图6所示,从图中可以看出,序列1和2,3、4和5,6和7熵值彼此接近,将熵值接近的子序列合成新的子序列,新子序列如图7所示。



从图7中可以看出,NEW1的波动频率较高,因此它有着非常大的随机性,很容易受随机因素的影响。选择多个输入和一个输出的RBF网络,输入变量可选为:待测点前3个小时的负荷值、前一天的负荷值、前两天的负荷值、前一周同一时间的负荷值、预测当日的平均温度、天气及日类型。NEW2几乎是以日为周期波动,随机因素对序列的影响不大,同样选择多个输入一个输出的RBF网络,输入变量可选为:待测点前3个小时的负荷值、前一天的负荷值、前两天的负荷值同一时间的负荷值。NEW3变化相对稳定,周期性不明显,选择一个多个输入多个输出网络,输出即为要预测的24小时负荷值,输入变量可选为:预测日前一天及前一周24小时的负荷值、预测当日的平均温度、天气及日类型。
基于上述分析,为每个新合成的子序列建立RBF神经网络预测模型,并将每个预测模型输出的值相加,得到最终预测值。
为验证EEMD-SE-GARBF预测模型的有效性,在同样的计算条件下分别使用RBF预测模型和GARBF预测模型对相同的用电负荷时间序列进行预测,结果如图8所示。

为了评判各预测模型的精确性,本文采用相对误差(RE)和平均绝对百分比误差(MAPE)指标来描述预测精度,结果如图9和表2所示。



通过分析可知,GARBF预测模型MAPE比RBF预测模型降低了3.94%,说明使用遗传算法对网络参数的优化使得预测精度有所提高。从图9中可以看出,本文中使用的EEMD-SE-GARBF组合预测模型相较于其他两种模型具有相对平稳且较小的相对误差,并且MAPE仅为2.41%,在预测精度上很明显要高于GARBF预测模型和RBF预测模型,说明在处理具有较强波动性的用电负荷时间序列中,对原始数据进行的平稳化预处理可以有效提高预测的精度。
5 结论
本文提出了一种基于EEMD-SE和GARBF神经网络的组合预测方法,利用EEMD分解法自适应地对负荷序列进行分解,结合样本熵对复杂度相似的子序列进行合并,并且针对RBF神经网络容易陷入局部最优问题,利用遗传算法优化网络参数。结果表明,所提出的EEMD-SE-GARBF组合预测模型可以很好地应用于短期电力负荷预测,具有广泛的应用价值。
参考文献
[1] 康重庆,夏青,刘梅.电力系统负荷预测[M].北京:中国电力出版社,2007.
[2] 李振华,许延春,李龙飞,等.基于BP神经网络的导水裂隙带高度预测[J].采矿与安全工程学报,2015,32(6):905-910.
[3] 李龙,魏靖,黎灿兵.基于人工神经网络的负荷模型预测[J].电工技术学报,2015,30(8):225-230.
[4] 杨茂,陈郁林.基于EMD分解和集对分析的风电功率实时预测[J].电工技术学报,2016,31(21):86-93.
[5] 王贺,胡志坚,陈珍,等.基于集合经验模态分解和小波神经网络的短期风功率组合预测[J].电工技术学报,2013,28(4):137-144.
[6] 茆美琴,龚文剑,张榴晨,等.基于EEMD-SVM方法的光伏电站短期出力预测[J].中国电机工程学报,2013,33(34):17-24.
[7] 张学清,梁军,张熙.基于样本熵和极端学习机的超短期风电功率组合预测模型[J].中国电机工程学报,2013,33(25):33-40.
[8] 彭显刚,胡松峰,吕大勇.基于RBF神经网络的短期负荷预测方法综述[J].电力系统保护与控制,2011,39(17):144-148.
[9] 王育飞,付玉超,孙路.基于混沌-RBF神经网络的光伏发电功率超短期预测模型[J].电网技术,2018,42(4):1110-1116.
作者信息:
高 强1,2,李易隆1,2,李大华1,2,白梓璇1,2
(1.天津理工大学 电气电子工程学院 天津市复杂系统控制理论及应用重点实验室,天津300384;
2.机电工程国家级实验教学示范中心,天津300384)

