文献标识码: A
DOI:10.16157/j.issn.0258-7998.190014
中文引用格式: 孙成,黄钰,朱剑平,等. 基于DFFT-WT-BP的光伏系统谐波检测[J].电子技术应用,2019,45(10):71-75.
英文引用格式: Sun Cheng,Huang Yu,Zhu Jianping,et al. Harmonic detection of PV power generation system based on DFFT-WT-BP[J]. Application of Electronic Technique,2019,45(10):71-75.
0 引言
随着现代光伏系统的发展,越来越多的光伏逆变器接入电网,随之产生的大量的谐波对于系统电能质量的污染十分严重[1]。FFT是传统的谐波检测算法,被广泛应用于光伏发电站的谐波检测[2]。但在工程应用中,采样非同步时,FFT存在较为明显的频谱泄露与栅栏效应[3],检测精度较低,难以准确识别间谐波与非稳态谐波[4]。为此许多学者们提出了各类改进FFT算法,如FFT与WT联合算法[5-7]、FFT与BP联合算法[8-10]等。但是,这些改进算法都只是针对某些谐波的检测有优势,难以处理实际的复杂谐波信号。本文提出了一种基于DFFT-WT-BP的谐波检测方法,该方法结合了FFT、WT和BP网络的优点,可以分析实际光伏并网逆变系统的复杂谐波信号,精度更高,实用性更强。
1 FFT算法
傅里叶变换的实质就是对信号进行加窗截断,从时域变换到频域进行分析[11]。考虑到汉宁窗频具有谱泄露较小的优点,因此截断窗函数选择汉宁窗。汉宁窗双谱线插值算法的频率、幅度的修正公式为[12]:

2 基于FFT的改进算法
2.1 基于FFT-WT的改进算法
分布式光伏并网逆变系统实际运行时会产生大量的突变信号或高频谐振,以及各种类型的噪声干扰。这些信号FFT难以处理,而WT适用于分析非稳态信号,弥补了前者的不足[13]。所以,学者们提出了一种将FFT与WT结合之后得到的能够综合两者优势的新算法(FFT-WT算法),具体流程如图1所示。主要思路为:利用WT将信号分解至不同的频带,利用FFT分析低频信号,利用小波分析高频信号。

然而,该算法是在已知谐波成分的基础上制定的,但在工程实际中面对的谐波信号是未知的,因此无法确定小波的分解层数以及所需要关注的频带。本文在前者的基础上,增加了FTT预分析的方法,提出了双重FFT与WT相结合(Wavelet-Double FFT,DFFT-WT)的改进方案:利用FFT获取谐波的粗略分布,以此推算出小波的分解层数和后续关注的频带,再使用WT将信号分离。对所关注的高频频带使用小波阈值消噪后分析与重构,获得高频分量的参数信息;对关注的低频频带使用加窗插值FFT分析,获得低频分量的参数信息。算法的主要流程如图2所示。

对比图1与图2所示流程图,可以看到,本节提出的DFFT-WT算法采取了预分析的方式,确定了分解层数与关注频带,理论上可以大大减少运算量,具有更高的精度与实用性。
2.2 基于FFT-BP的改进算法
FFT对于谐波的检测精度不高,而BP神经网络拥有强大的非线性映射能力和自学习能力,能够弥补前者的不足。对此,一些学者将FFT与BP神经网络相结合(以下简称FFT-BP算法),提升了对于谐波检测的精度,具体流程如图3所示。

本节将学习率、动量因子和激励函数一同参与网络的调节,构建的BP神经网络结构图如图4所示,其训练步骤如下:
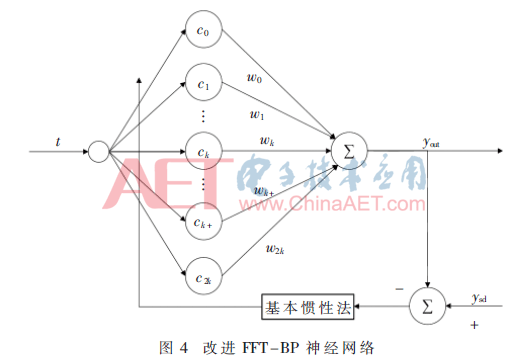
BP网络的输入设为ti(i=1,2,…,N),网络的激励函数c(t)表示为:

在仿真研究时发现,因为BP网络寻求的是全局的最优解,所以在多种谐波共同构成的复杂谐波信号中,BP网络为了达到整体误差的最小,会在迭代时自动“牺牲”小信号分量的精度。所以说,改进后的FFT-BP算法对于复杂信号中的间谐波弱分量的检测能力仍然是不够的。
3 基于DFFT-WT-BP的联合检测方案
DFFT-WT算法能够同时处理稳态与非稳态谐波,但精度仍然有提升的空间,改进后的FFT-BP算法对于间谐波小信号的检测能力不足,且无法检测非稳态谐波。在研究了FFT算法、WT算法和BP神经网络的基础上,联系前面提出的两种改进算法,本文提出了基于DFFT-WT-BP的复杂信号检测算法,具体流程如图5所示,主要步骤如下:
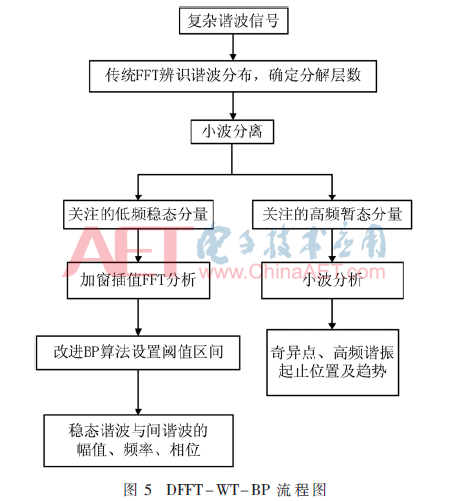
(1)FFT算法预分析,得到小波的分解层数以及需要关注的频带。
(2)根据上一步计算获得的分解层数,选取合适的离散小波将复杂信号粗略分离,得到关注频带信息。
(3)对上一步分解之后得到的关注高频分量进行阈值去噪后分析,必要时重构,得到高频谐波的起止时刻以及振幅;得到关注的低频分量,利用加窗插值FFT得到全部的稳态谐波个数及粗精度的频率、幅度和相位。
(4)将上一步得到的谐波总个数设定为BP网络中神经元的个数,将得到的粗精度谐波频率设定为BP神经网络中谐波频率的初始值。前文提到,BP网络在运算复杂信号时,对于间谐波弱信号的检测能力不足,但是本方案的前三步已经让BP网络获得了较好的初值,因此在其基础上,增加BP网络迭代时±1%频率阈值区间、±5%幅度阈值区间和±10%相位阈值区间,进行优化运算,最终得到稳态分量高精度的频率、幅度与相位。
与传统的检测算法以及各类改进检测算法相比,DFFT-WT-BP算法主要作出了以下5点改进:
(1)利用FFT预分析未知信号,可以快速得出分解层数和关注谐波所处的频带,只需要对特定的频带作处理,节省了工作量。
(2)由于已经通过预分析的方法确定了关注频带,因此只需要对信号作粗略的分解,规避了分解层数过多时检测速度与精度受到影响的问题。
(3)将已经处理过的粗精度谐波参数送入BP网络进一步优化,减少了迭代时间,提升了检测精度,增加了对间谐波的识别能力。
(4)将BP网络的学习率与动量因子一起参与神经网络的调整,减少了运算时间,提升了检测精度,实现了对间谐波的检测。
(5)增加了频率、幅度和相位的迭代区间,限制了运算时的搜索区域,规避了间谐波迭代时为了“迎合”全局的误差最小值而发生偏移。
4 仿真分析
4.1 与FFT-BP算法的对比
由2.2节分析可知,FFT-BP算法不好处理复杂信号中的间谐波,为了体现DFFT-WT-BP算法的优势,在信号模型中仅加入整数次稳态谐波分量,获得FFT-BP算法与DFFT-WT-BP算法对于整数次谐波的检测结果。设谐波采样信号为:

由FFT预处理后,设定神经元个数为5个,取基波频率为50 Hz,设定BP网络初始的频率学习率为0.02,幅度与相位的学习率为0.1,动量因子设定为0.6,并按2.2节所述的规则进行调整。获得的幅度和相位的对比见表1、表2,误差曲线的对比如图6、图7所示。可以看出,FFT-BP算法与DFFT-WT-BP算法在该类信号条件下,幅值与相位的检测误差均在10-5~10-4,精度并没有明显差异,但FFT-BP算法的运算次数为1 871次,DFFT-WT-BP算法的运算次数为672次,运算时间有很大的差距。可以得出,DFFT-WT-BP算法与FFT-BP算法相比,迭代次数更少,效率更高。




4.2 与FFT-WT算法的对比
本文构建了如式(7)所示的复杂信号,其包括50 Hz的基频信号以及频次比为1.6:3:3.1:5:5.2:7:8.2:11的稳态信号,其幅度比为100:8:50:10:50:5:50:30:15:30;含有一个最大幅度为80 V的高频衰减信号;包含一个正态分布的随机噪声。对该模型采取FFT-WT算法以及DFFT-WT-BP算法分别仿真分析。

根据图6所示流程图,得到高频衰减信号如图8所示,其最大幅度为80 V,起始位置为0.2 s,与预定结果一致,满足检测要求。得到全部的稳态谐波与间谐波粗精度的频率、幅度与相位信息如图9所示,经过BP网络计算后获得的优化结果与FFT-WT算法的结果分析结果比对见表3~表5。





由表3~表5的数据对比得到:
(1)FFT-WT算法检测频率的误差分布在10-4~10-3,DFFT-WT-BP算法检测频率的误差分布在10-6~10-5。
(2)FFT-WT算法检测幅度的误差分布在10-4~10-2,DFFT-WT-BP算法检测幅度的误差分布在10-5~10-4。
(3)FFT-WT算法检测相位的误差分布在10-4~10-2,DFFT-WT-BP算法检测相位的误差分布在10-5~10-4。
能够推出,在处理电网实际的复杂信号时,DFFT-WT-BP算法不但准确检测出了非稳态分量的主要参数,而且用设定阈值区间的方法规避了FFT-BP算法的固有缺陷,拥有了对间谐波弱信号的检测能力,对于稳态分量整体的检测精度比FFT-WT算法高出了1~2个数量级。
5 结论
针对光伏系统的谐波信号,本文在对现有的FFT-WT算法和FFT-BP算法改进的基础上,提出了联合的DFFT-WT-BP算法。经仿真验证,本文提出的DFFT-WT-BP算法对于光伏系统中由稳态的谐波与间谐波分量、非稳态分量和各种噪声叠加而成的复杂信号有着很好的检测效果。理论与仿真结果表明,DFFT-WT-BP算法精度高,实时性好,适应能力强,能够满足实际的检测需求。
参考文献
[1] 薛萍,朱琳琳,王宏民.基于准同步采样光伏发电系统谐波分析方法[J].电子技术应用,2015,41(11):121-123.
[2] LIU D,YANG Z,HE Y,et al.Harmonic analysis of power system based on Rife-Vincent self-convolution window triple-spectral-line interpolation FFT[J].Journal of Electronic Measurement & Instrumentation,2016,30(9):1351-1356.
[3] 李平,李源,孔银昌.一种加Nuttall窗三谱线插值FFT谐波检测算法[J].电子技术应用,2017,43(5):41-43.
[4] 翟晓军,周波.一种改进的插值FFT谐波分析算法[J].中国电机工程学报,2016,36(11):2952-2958.
[5] 朱翔,解大,高强,等.基于FFT和db20小波变换的电力系统谐波联合分析策略[J].电力系统保护与控制,2012,40(12):62-65.
[6] 房国志,杨超,赵洪.基于FFT和小波包变换的电力系统谐波检测方法[J].电力系统保护与控制,2012,40(5):75-79.
[7] EBRAHIM M A,ELYAN T,WADIE F,et al.Optimal design of RC snubber circuit for mitigating transient overvoltage on VCB via hybrid FFT/Wavelet Genetic approach[J].Electric Power Systems Researc,2017,143:451-461.
[8] 王凯亮,曾江,王克英.一种基于BP神经网络的谐波检测方案[J].电力系统保护与控制,2013(17):44-48.
[9] 曹英丽,尹希哲.基于BP神经网络和全相位快速傅里叶变换的电力系统谐波检测技术研究[J].现代电子技术,2017, 40(1):133-136,141.
[10] 邢晓敏,商国敬,徐新.基于线性神经网络的谐波检测方法研究[J].电测与仪表,2014,51(22): 40-43.
[11] OUYANG M X. Applications of addbBlackman window function in FFT[J].Southern Metals,2012(5):51-53,60.
[12] KANG W,LI N,ZHANG J,et al.An improved harmonic analysis algorithm of multi-spectrum-line interpolation FFT[J].Electrical Measurement & Instrumentation,2016,53(10):8-15.
[13] 孙曙光,庞毅,王景芹,等.一种基于新型小波阈值去噪预处理的eemd谐波检测方法[J].电力系统保护与控制,2016:44(2):42-48.
作者信息:
孙 成1,黄 钰2,朱剑平1,张保健1,张志远1,王雅静2
(1.上海金智晟东电力科技有限公司,江苏 南京210000;2.山东理工大学,山东 淄博255000)

