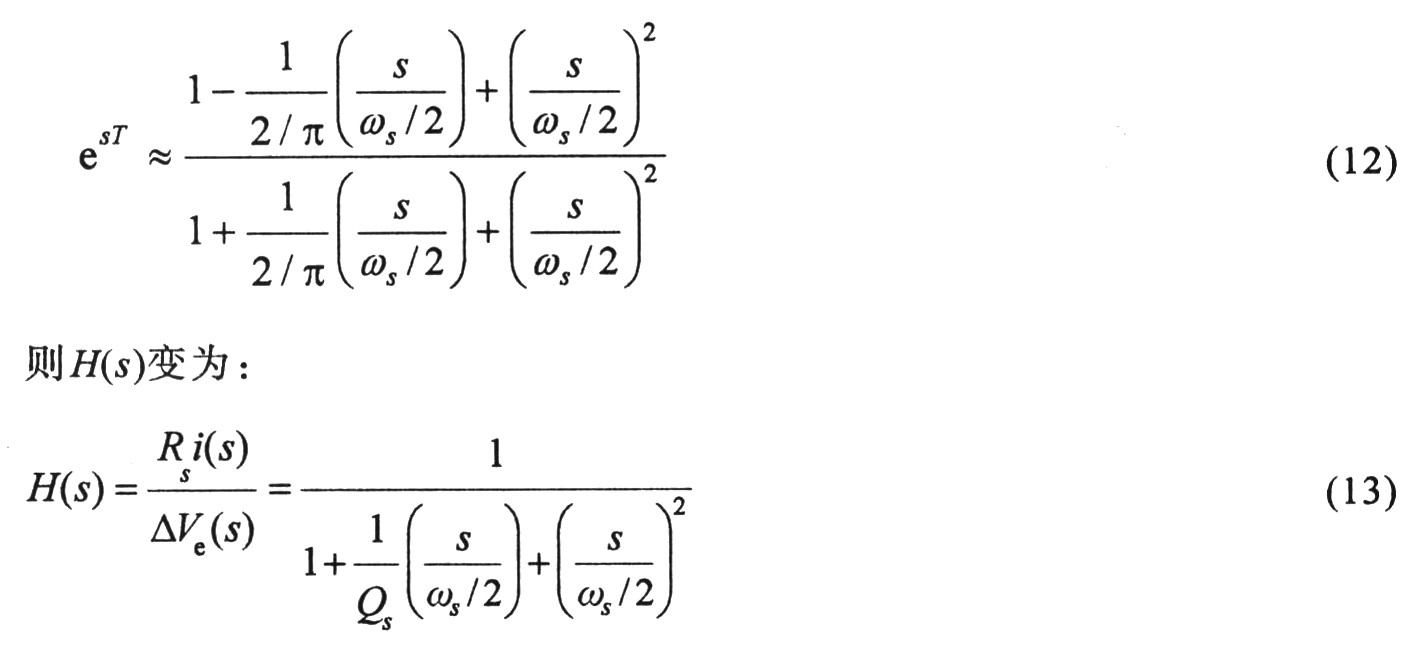DC-DC开关电源因体积小,重量轻,效率高,性能稳定等优点在电子、电器设备,家电领域得到了广泛应用,进入了快速发展期。DC-DC开关电源采用功率半导体作为开关,通过控制开关的占空比" title="占空比">占空比调整输出电压。其控制电路拓扑分为电流模式和电压模式,电流模式控制因动态反应快、补偿电路简化、增益带宽大、输出电感小和易于均流等优点而被广泛应用。电流模式控制又分为峰值电流" title="峰值电流">峰值电流控制和平均电流控制,峰值电流的优点为:1)暂态闭环响应比较快,对输入电压的变化和输出负载的变化瞬态响应也比较快;2)控制环易于设计;3)具有简单自动的磁平衡功能;4)具有瞬时峰值电流限流功能等。但是峰值电感电流可能会引起系统出现次谐波振荡,许多文献虽对此进行一定的介绍,但都没有对次谐波振荡进行系统研究,特别是其产生原因和具体的电路实现,本文将对次谐波振荡进行系统研究。
1 次谐波振荡产生原因
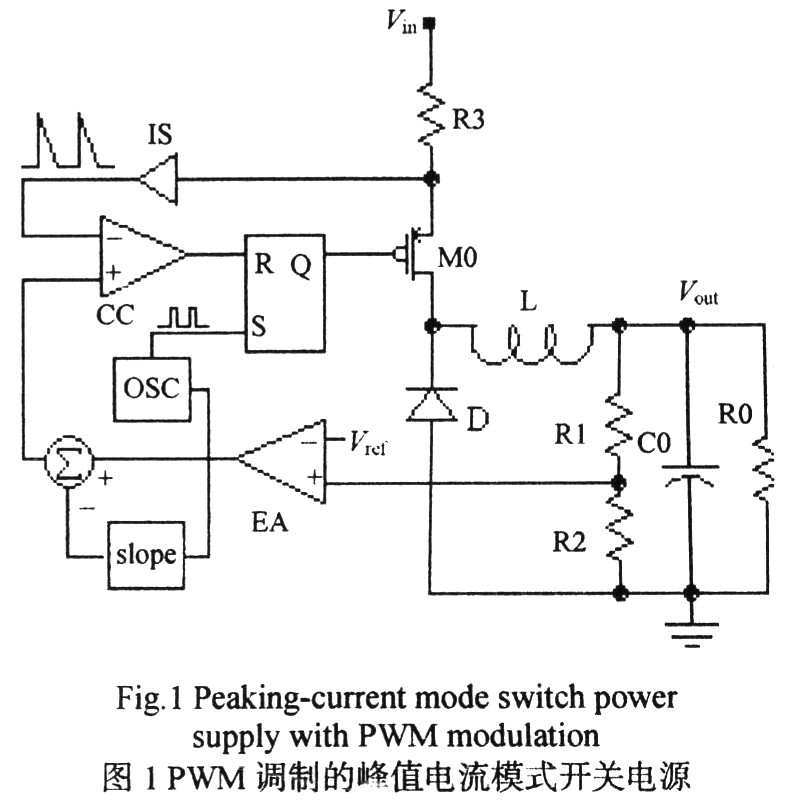
以PWM调制峰值电流模式开关电源为例(如图1所示,并给出了下斜坡补偿" title="斜坡补偿">斜坡补偿结构),对次谐波振荡产生的原因从不同的角度进行详细分析。
查看原图(大图)
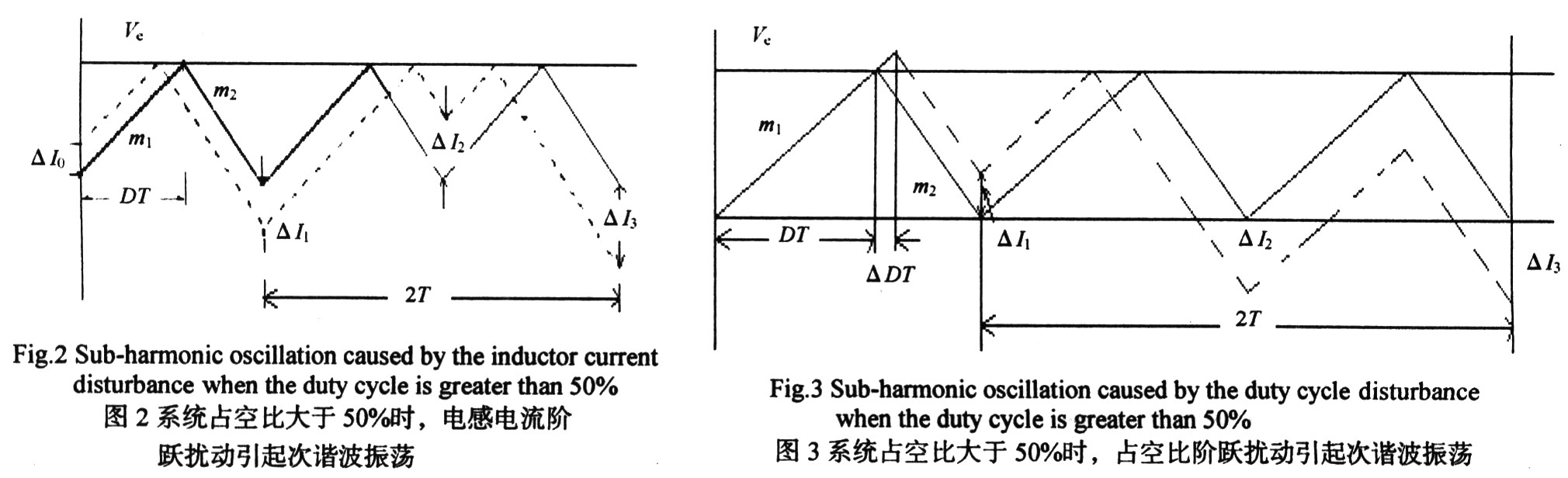
对于电流内环控制模式,图2给出了当系统占空比大于50%且电感电流发生微小阶跃△厶时的电感电流变化情况,其中实线为系统正常工作时的电感电流波形,虚线为电感电流实际工作波形。可以看出:1)后一个时钟周期的电感电流误差比前一个周期的电感电流误差大,即电感电流误差信号振荡发散,系统不稳定;2)振荡周期为开关周期的2倍,即振荡频率为开关频率" title="开关频率">开关频率的1/2,这就是次谐波振荡名称的由来。图3给出了当系统占空比大于50%且占空比发生微小阶跃AD时电感电流的变化情况,可以看出系统同样会出现次谐波振荡。而当系统占空比小于50%时,虽然电感电流或占空比的扰动同样会引起电感电流误差信号发生振荡,但这种振荡属于衰减振荡。系统是稳定的。
查看原图(大图)
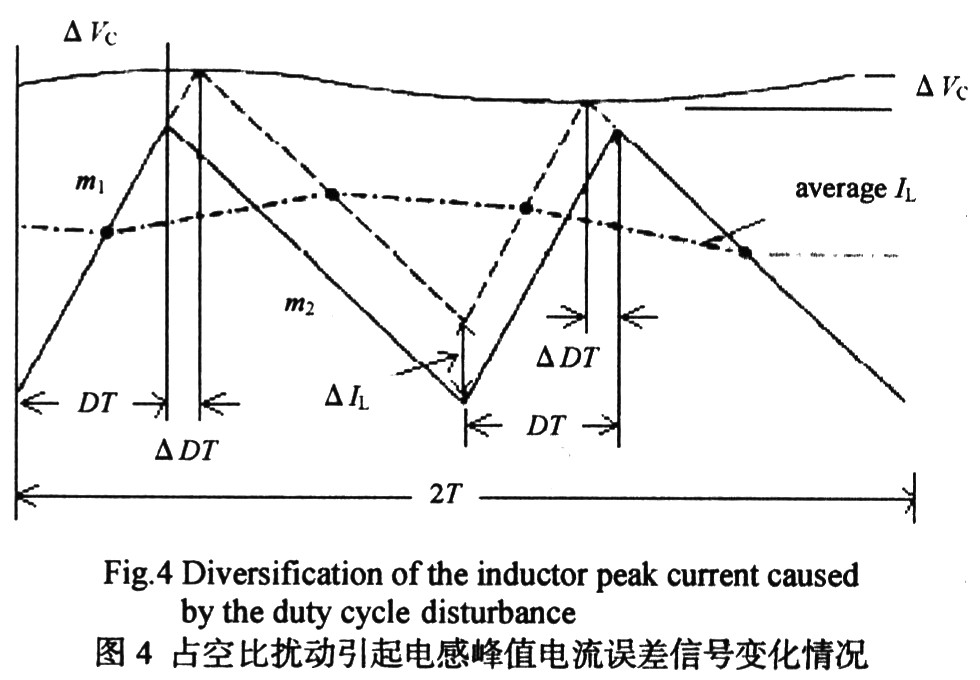
前面定性分析了次谐波振荡产生的原因,现对其进行定量分析。针对图1,图4给出了占空比扰动引起电感峰值电流误差信号变化情况,其中Vc为误差运放的输出信号,当功率管MO导通即电感电流线性上升时,Vc随之增加,反之当功率管M0关断时,Vc随之减小。从图4可以看出当占空比在连续2个时钟脉冲下存在不对称时,系统将出现次谐波振荡。现推导△Vc与△IL的关系,占空比扰动△D引起电感电流与误差运放输出电压的变化值分别如式(1)和(2)所示,由式 (1)和(2)可推导出Vc与△IL的关系如式(3)所示:
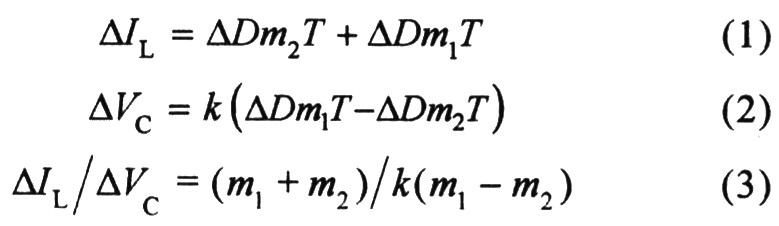
查看原图(大图)
式中:T为开关周期;m1为峰值电流上升斜率;m2为峰值电流下降斜率绝对值;七代表采样电阻。
由于次谐波振荡频率为开关频率的1/2,因此在1/2开关频率处的电压环路增益将直接影响电路的稳定性。现推导图1的电压环路增益,在误差运放输出端叠加斜坡补偿后,设误差电压从△Vc变为△Ve,从而可推出△Vc与△Ve的关系,如式(4)所示。由式(3)和(4)可得式(5),在稳态时可推出式 (6),将式(6)代入式(5)消去m1,得式(7):
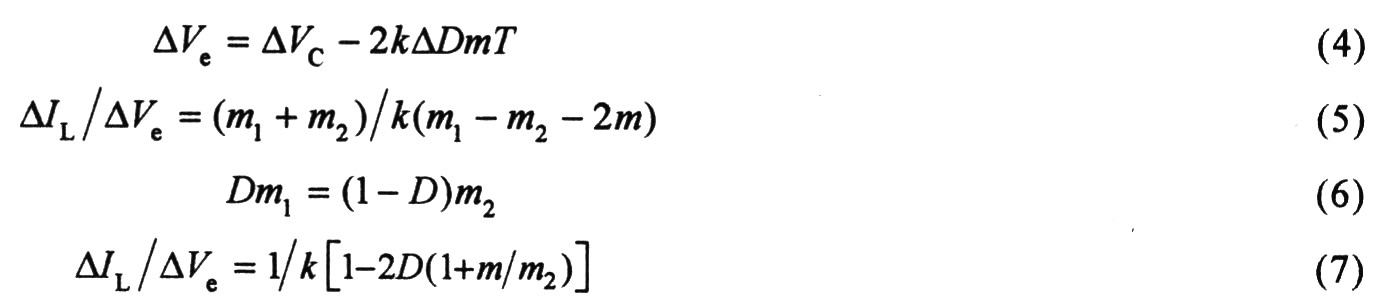
查看原图(大图)
查看原图(大图)
式中:m为下斜坡斜率;2表示次谐波振荡周期是开关频率的2倍。
从图4可以看出△IL是周期为2T的方波,则第1个次谐波振幅应乘以4/π。假设负载电容为C,则从误差运放输出端到电源输出端的小信号电压增益为
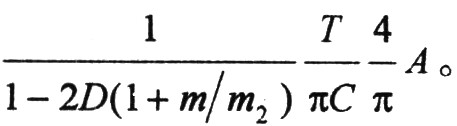
设误差运放电压增益为A,则电压外环环路增益为
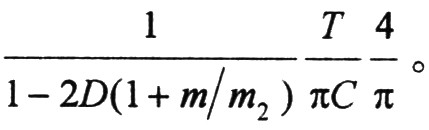
由环路稳定性条件可知:在l/2开关频率处,环路相位裕度为零,此时若环路增益大于l,系统就会发生次谐波振荡,因此误差运放的最大增益为:
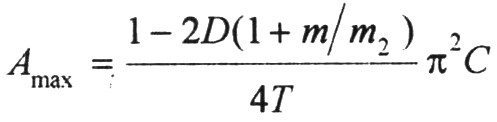 (8)
(8)
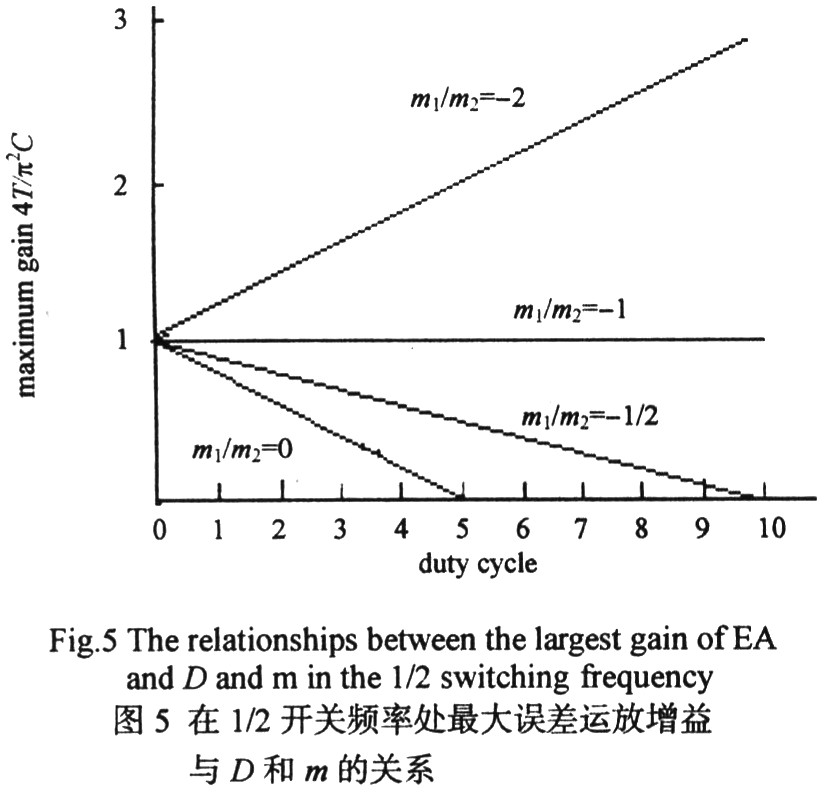
由式(8)可以明显看出,误差运放的最大增益是占空比D和斜坡补偿斜率m的函数,归一化的误差运放最大增益与D和m的关系如图5所示。可以看出:m=O(无补偿)时,由于运放增益不能小于O,当占空比大于或等于50%时,系统就会出现次谐波振荡;m=一m2/2时,D=100%才出现次谐波振荡,但在实际电路中D<100%时就会出现振荡;m=一m2时,误差运放最大增益与占空比无关。当继续增大m时,对环路的稳定性影响不大,但过补偿会影响系统瞬态响应特性。
上文研究了电感电流信号变化波形对次谐波振荡产生的原因及解决办法,现从s域(或频域)角度对其进行更深入的研究。设采样电感电流i,通过采样电阻Rs转化成电压,i(k)表示第k时钟下的电流扰动量,△Ve(k+1)为第k+1时刻的电压控制扰动量,得采样保持的离散时间函数:
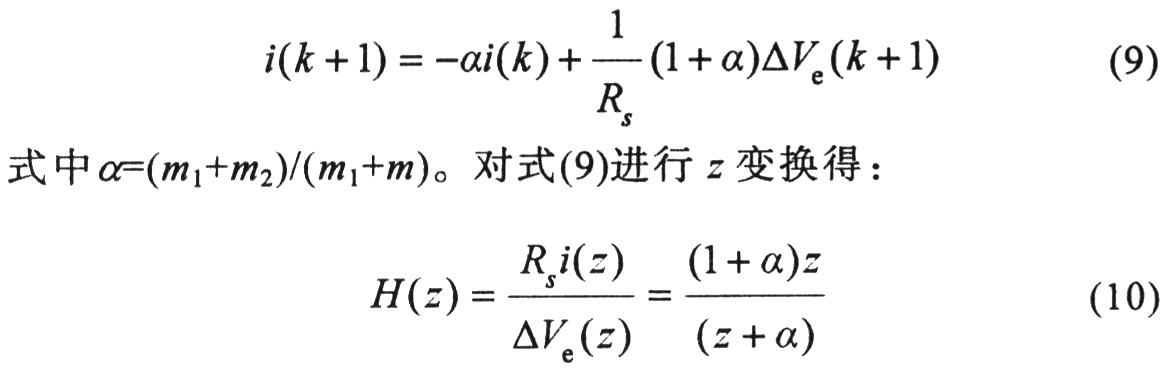
查看原图(大图)
由式(10)可知当没有斜坡补偿,且m1
查看原图(大图)
式中s表示频率。esT可用PadE可用Pade进行二阶近似:
查看原图(大图)
查看原图(大图)
式中Qs=2/[π(2/α-1)],即阻尼系数为1/Qs=[π(m1-m2+2m)]/[2(m1+m2)]。式(13)即为电流环传递函数,斜坡补偿前,当m1
2 斜坡补偿方式及电路实现
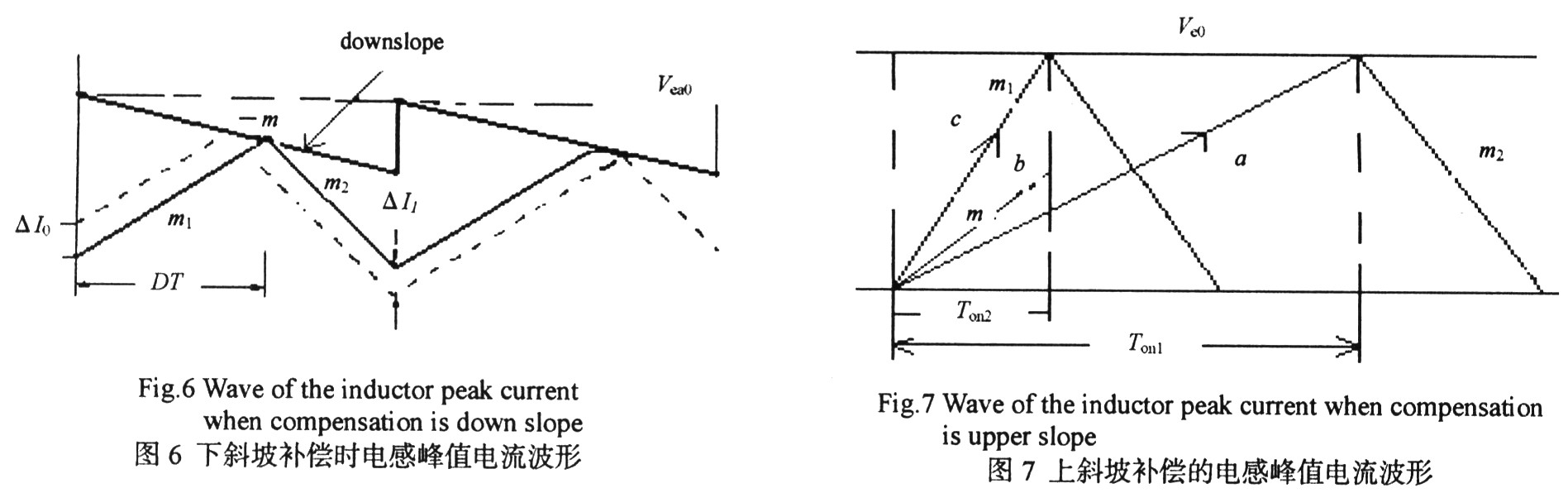
前文从几个方面研究了次谐波振荡产生的原因,并且指出斜坡补偿能防止系统出次谐波振荡,现研究补偿方式及其具体电路实现。开关电源斜坡补偿分为上斜坡补偿与下斜坡补偿2种方式。图6为下斜坡补偿原理,给出了下斜坡补偿时占空比大于50%的电感峰值电流波形(电流微小扰动作为激励信号)。与图2相比,仅Ve 从水平直线改为下斜坡。从图6可以看出,引入斜坡补偿后,电流误差信号每经过一个时钟周期,幅度成比例衰减,最后消失。图7为上斜坡补偿原理,给出了占空比大于50%的电感峰值电流波形。其补偿原理就是在电感峰值电流a上叠加上斜坡补偿电流b,形成检测电流c,使占空比小于50%,稳定系统。由于上斜坡补偿电路实现相对简单,一般采用上斜坡补偿。
对于斜坡补偿,斜率越大,振荡衰减越快,但补偿斜率过大,会造成过补偿。过补偿会加剧斜坡补偿对系统开关电流限制指标的影响,从而降低系统的带载能力;另一方面,过补偿会影响系统瞬态响应特性。通常选择斜坡补偿斜率需根据需要折中考虑。对于Buck和Flyback转换器,补偿斜坡一般取峰值电流下降斜率 m2即Vout/L,由于输出电压恒定,所以补偿值便于计算并恒定;对于Boost电路,补偿斜坡也一般取峰值电流下降斜率m2,即(Vout- Vin)/L但由于输入电压随电网变化,从而要求补偿值跟随输入电压的变化,此时若为了电路设计简单,强迫斜坡斜率固定,则可能出现过补偿或欠补偿现象,降低电路性能并导致波形畸变。
查看原图(大图)
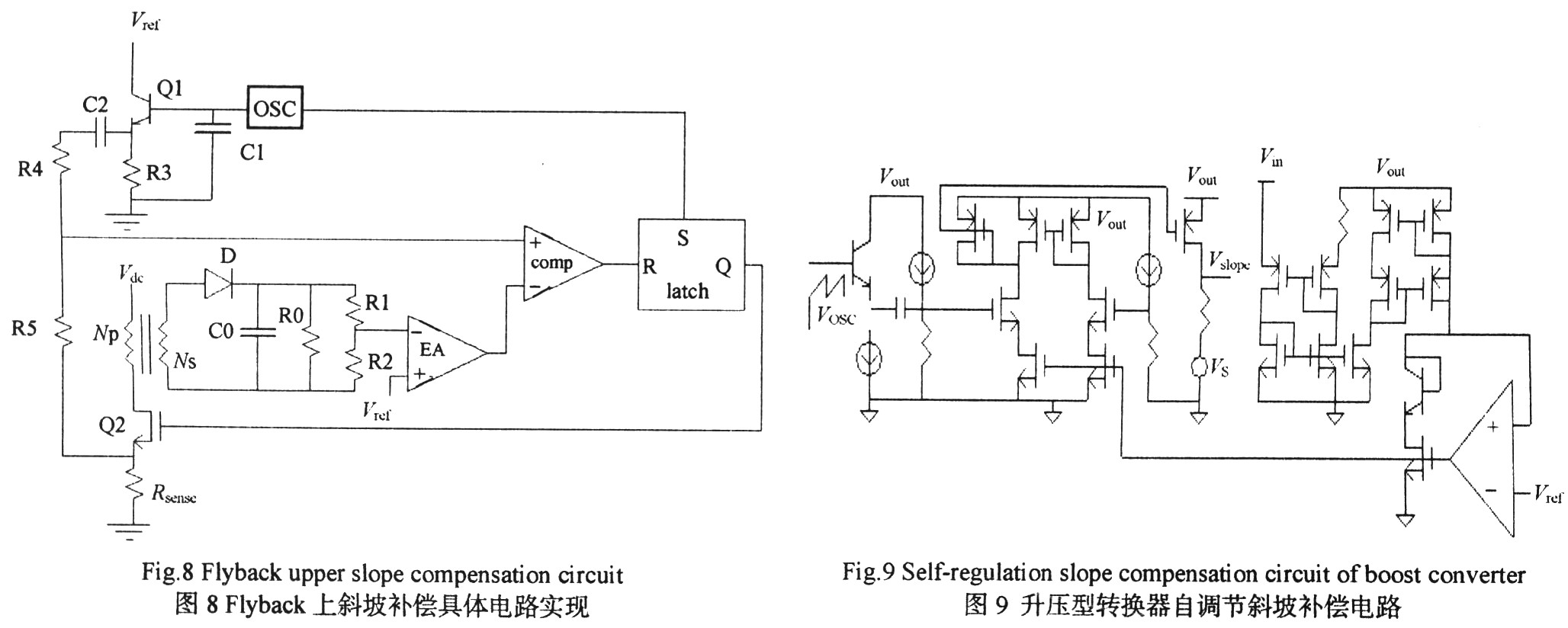
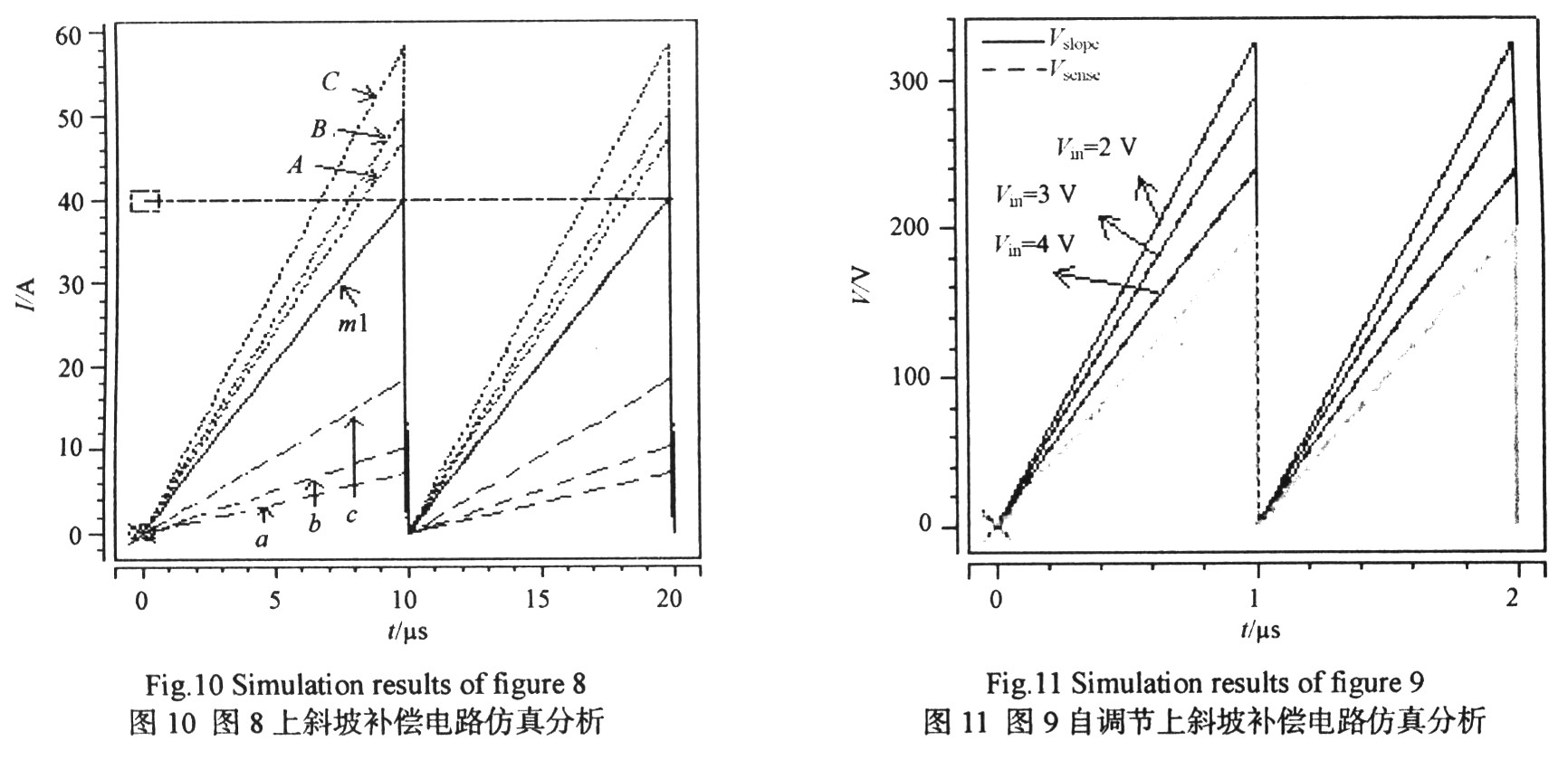
因Buck与Flyback转换器斜坡补偿原理电路实现基本相同,因此本文只给出了一种上斜坡补偿的Flyback斜坡补偿电路(图8所示)。图9为本文第二作者提出的一种升压型转换器自调节斜坡补偿电路。采用Hspice仿真软件分别对图8和图9进行仿真,仿真结果分别如图10和图11所示。图10的振荡器频率为100 kHz。m1为检测电流曲线,其从0慢慢上升到40μA。虚线a,b和c代表具有不同斜率的斜坡补偿信号,线A,B和C分别为叠加后的曲线。从图10可看出:通过改变电阻R5和R4的比值,可以得到具有不同斜坡的补偿信号。图11中,Vsense为电感上的峰值电流流过检测电阻所产生的电压,Vslope 为经上斜坡补偿后的检测电流流过检测电阻所产生的电压。从图11可以看出,不同的输入电压对应不同的补偿斜坡,并且斜坡变化与(Vout-Vin)的变化成正比即达到了自调节功能。
查看原图(大图)
查看原图(大图)
3 结论
本文对峰值电流模式开关电源的次谐波振荡从定性和定量2个角度分别进行了系统研究,当占空比大于50%时,系统的电流环在1/2开关频率处出现振荡,引入斜坡补偿后能保证电流环路增益的传输函数在1/2开关频率处具有较好的相位裕度,保证系统稳定。最后分析了上斜坡补偿和下斜坡补偿2种避免次谐波振荡的方法,并基于3种最基本的开关电源拓扑(Buck,Flyback和Boost)给出了具体的斜坡补偿电路及仿真结果。