摘  要： 设计了随动控制型齿轮测量系统齿轮误差计算模型。利用随动控制系统作为测量齿轮螺旋线偏差的控制方式，以被测齿轮的螺旋线偏差为研究对象；对被测齿轮的实际螺旋线建立分析模型，对其跟踪轨迹进行螺旋线拟合，并实现螺旋线偏差的计算。本模型能够在简化系统运动控制方式和结构情况下，有效地测量齿轮螺旋线误差，并对建立的分析模型的准确性进行了验证。
关键词： 随动控制；跟踪测量；螺旋线拟合

　齿轮测量技术的发展历程以齿轮精度理论的发展为前提，为了提高测量齿轮误差的精度，齿轮测量技术先后出现了机械展成式测量技术、齿轮整体误差测量技术、CNC坐标测量技术及非接触测量技术。前三项测量技术都采用精密运动控制作为测量齿轮偏差的控制基础，运动控制系统对齿轮误差测量精度有很大影响。
随动控制方式[1]的提出，丰富了现有齿轮误差测量控制系统的控制方式，简化了测量仪器的硬件结构，并且能够实现跟踪实时测量。
　基于随动控制系统的齿轮测量仪结构如图1所示。在测量过程中，被测齿轮1绕其回转轴匀速转动，与被测齿面接触的电感传感器测头2有一个位移变化量，使得电感传感器对应有一个位移输出量。为使电感传感器3的输出稳定在零附近的一定阈值内，控制测量滑块4带动电感传感器做轴向运动，电感传感器测头2跟随被测齿轮沿其中心轴线方向作相应的跟随移动，此时，电感传感器测头相对于被测齿轮的运动轨迹即为被测螺旋线(实际曲线)。

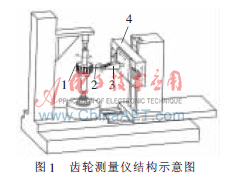
　本文在采用随动控制系统作为测量齿轮误差的基础上，利用随动控制特性，相对于被测齿轮做跟随运动并进行点测量，利用各个测量点对被测齿轮的螺旋线进行拟合，从而实现齿轮螺旋线偏差的测量。
1 模型建立
　被测齿轮绕其中心轴作匀速旋转运动，与被测齿轮表面相接触的一点同时沿与中心轴线平行方向匀速移动，这一点在此被测面上的运动轨迹即为螺旋线(如图2)。

　在随动控制系统的作用下，电感传感器在Z轴方向上的跟随运动是变速运动，所以在此测量坐标系中的螺旋线参数方程[2]为：

    最后经过整理得到：

3 实验仿真与分析
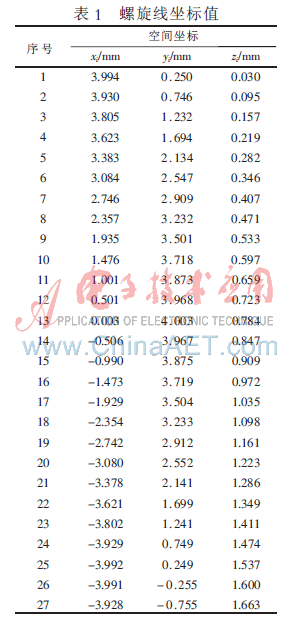
　已知一圆螺旋线中的制造误差δ=±0.003，它的参数方程R=4.000，ω=2.0，x、y、z分别为已知螺旋线空间坐标值，Δ为各个坐标点的偏差值，实验仿真数据如表1所示。
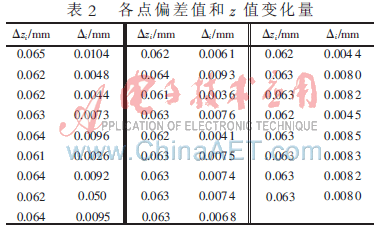
　首先对参数R和ω进行估计，然后利用迭代法[6]得到R=3.999 8和ω=2.002 1，最后利用公式(15)求得各点的偏差如表2所示，然后求得螺旋线偏差Δmax=0.007 8 mm，其中Δzi=zi+1-zi。

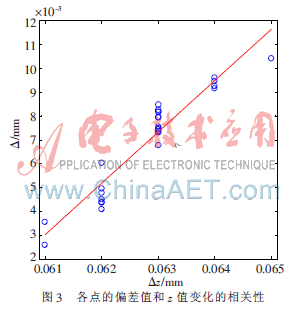
　各点的偏差值和z值的相关性如图3所示。从图3可以发现，螺旋线上某点的偏差值和z轴方向上z值的变化量存在对应关系，当偏差值比较大时，z轴方向上z值的变化量也跟着变大；当偏差值比较小时，z轴方向上z值的变化量也跟着变小，它们的相关系数为0.951，反映出随动控制和跟踪测量的特点。

　本文从螺旋线的形成原理作为问题研究的切入点，根据随动控制系统的控制特点，提出了一种新的齿轮螺旋线拟合的方法，然后利用最小二乘法求得拟合螺旋线的相关参数，最后得到实际被测螺旋线的偏差。从实验结果看，利用随动控制系统进行齿轮螺旋线的拟合，再结合控制系统对螺旋线进行误差评定，可以作为一种被测齿轮螺旋线精度估计的有效方法。
参考文献
[1] 赵军，刘维，马忠祥，等.基于随动控制的齿轮测量方法[J].工具技术，2010，44(4)：75-78.
[2] 陈基伟.螺旋线拟合应用研究[J].北京联合大学学报(自然科学版)，2008，22(4)：2-4.
[3] 王解先，徐志京.三种坐标间转换的雅可比矩阵数值导数计算方法[J].大地测量与地球动力学，2004，24(4)：1-2.
[4] 沈永欢，梁在中，许履瑚，等.实用数学手册[M].北京：科学出版社，2002.
[5] 张泰昌.齿轮检测500问[M].北京：中国标准化出版社，2007.
[6] 朱静芬，韩丹夫.“牛顿类”迭代的收敛性和误差估计[J].浙江大学学报(理学版)，2005，32(6)：1-3.