配浆浓度是决定造纸生产工艺质量的重要指标。近年来，随着制浆造纸技术的飞速发展，业内对配浆浓度控制的精度提出了越来越高的要求。然而由于配浆浓度控制过程中，工艺参数常常发生较大变化，系统模型难以建立，传统控制器不能始终保持最优运行，有时甚至出现稳定性问题，导致现有配浆浓度控制手段存在一定的盲目性。因此提高配浆浓度的精度对节约成本、提高生产质量具有十分重要的意义[1]。

1 工艺描述
    造纸行业配浆系统主要完成配浆浓度、流量大小的测量与控制。草浆、木浆、损配浆按照一定的配比进入混合管然后送往纸机，另外在混合池里还要按比例加入一些化学添加剂和染料。该流程中各种浆料分别通过各自的浓度控制回路对其浆浓度进行独立调节控制,因此浓度控制回路效果直接决定了最终的配浆结果[2]。
    浓度控制回路工艺如图1所示，浓度控制由调节稀释水量大小实现，流量大小由手动阀门粗调。配浆浓度测量采用刀式传感器，流量测量采用电磁流量计，浓度控制执行器采用电动调节阀，浓度现场控制器是以单片机为核心、配以EPROM及实时时钟构成的微控制器。对于间断配浆过程，当设置一次配浆绝干量后，配浆单元自动启动抽浆泵工作，从浆池中抽取混合料，同时开启稀释水阀门，调节配浆浓度。由于从浆池中抽取混合料的速度基本稳定，因而稀释水流量直接决定了最终的配浆浓度，混合料与稀释水混合后，累计以配浆绝干量计算，当累计配浆绝干量与设置的一次配浆总量相等时，自动停止抽浆泵工作。

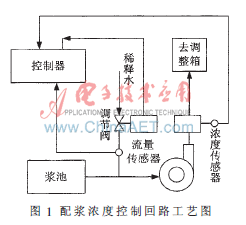
    为了保证配浆生产过程中，混合料浓度精度达到工艺要求，同时混合料浓度具有一定的抗干扰能力，其控制系统必须满足以下要求:通过调节稀释水阀门的开度，保证配浆浓度的控制精度在±0.08%内。
2  控制系统分析及结构
    由于配浆浓度控制系统具有较强的非线性和时变性，且造纸生产过程参数在生产过程中常常受到温度、湿度的影响，很难构造出一个精确的数学模型，因此，采用常规控制往往出现频繁波动，难以跟踪给定混合料浓度，无法取得较好的运行效果。通过对配浆工艺研究分析，本文提出一种基于智能控制的双闭环浓度控制方法，其控制原理如图2所示。该系统是由模糊遗传算法、神经网络PID、控制阀组及传感器组成的一种直接数字反馈串级控制系统。

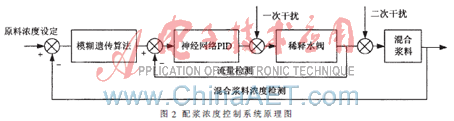
    该控制系统由内外两个闭环控制构成，外环为浓度控制环，内环为流量控制环。首先，浓度控制系统利用混合料浓度设定值和混合料浓度检测值计算得到系统浓度偏差，以其作为浓度控制环路的输入，通过模糊遗传控制器计算得到最优浓度调节量；然后，将该浓度调节量通过查表方式转换为相应的稀释水流量增量，作为流量控制环的输入，内环通过调节稀释水流量达到调节混合料浓度的目的，利用神经网络PID模块对稀释水浓度进行调节，始终保证混合浆料浓度满足工艺要求。
3 基于模糊遗传算法的外环控制器设计
    在配浆浓度控制系统中，由于受到添加原料、开关浆池闸门等突发因素的影响，采用传统的控制方法往往难以得到良好的作用，很难同时兼顾稳定控制、提高精度、抑制超调的要求。而且配浆浓度控制系统中，浓度传感器检测值会随着具体环境、季节、昼夜变化产生漂移，而传统模糊系统的隶属函数等参数很难自动调整，难以适应这些变化。因此本文采用模糊控制器对配浆浓度变化进行模糊推理，同时采用遗传算法对模糊控制器的参数进行自适应调整，从而得到最优的稀释水流量。
3.1 模糊控制器的设计
    根据实际生产工艺的需要，模糊控制器根据当前混合料浓度的检测值和设定值之间的偏差及其偏差变化率、模糊规则经推理得到最优的稀释水流量设定值。混合料浓度模糊控制模块的输入变量为混合料浓度与设定值的偏差e及其变化率ec，输出变量为稀释水流量的增量Δu。
　　本控制器中，浓度偏差e [-10%, +10%]，论域E＝{-7,-6,-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5,6,7}，模糊变量的词集选择为{NL，NM，NS，O，PS，PM，PL}。浓度偏差变化率 ec∈[-0.4%/s,0.4%/s]，论域为EC ={-4,-3,-2,-1,0,1,2,3,4}，EC的模糊变量为{NL，NS，O,PS，PL}。
    类似地,稀释水流量增量输出Δu∈[-2m3/s,2m3/s]，论域U＝{-6，-5,-4,-3,-2,-1,0,1,2,3,4,5，6}，U的模糊变量为：{NL，NM，NS，O，PS，PM，PL}。
    根据现场调节的经验发现,浓度偏差变化率ec仅在较大时方能反映出混合料浓度的变化趋势。因此，控制增量U与偏差E的关系较为紧密，而EC则主要作为U的一个辅助参考变量。本模糊控制器把实际的控制策略归纳为如表1所示的控制规则表。

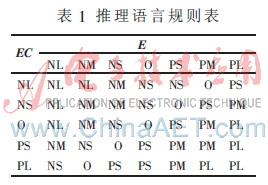
    为了抑制传感器检测中可能出现的异常值，本文对于输入输出变量、隶属度函数均采用如下的梯形函数。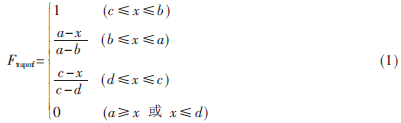

    由上述所设计的模糊推理规则及隶属度，采用Mamdani模糊推理的重心法进行解模糊，得到模糊控制的查询表如表2所示。系统将浓度偏差e及其变化率ec模糊化后求得E、EC，通过查询表，得到控制输出U，并将此值经过清晰化接口，求得稀释水流量的增量Δu。

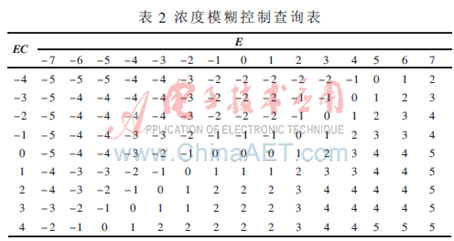
3.2 基于遗传算法的隶属度选择
    遗传算法(GA)具有搜索快速、易实现和计算效率高的优点[3]，非常适合在配浆浓度控制系统中。
3.2.1算法思路及步骤
　 本文在模糊算法的设计中采用了梯形隶属度函数，其形式由4个参数确定，由模糊算法的3个输入变量各自的梯形隶属度函数参数，共同构成了遗传算法的解空间。根据检测环境选择适应度函数，通过个体的变异搜索，寻找使得适应度函数最优的隶属度函数解，即得到最优的模糊算法结构。利用遗传算法选取隶属度，其实现步骤为：
　(1)首轮随机产生n个模糊隶属度参数个体，组成初始种群，非首轮随机产生n-1个个体，第n个个体为以前一代种群的最优个体，组成新一轮迭代的起始种群。
    (2)利用适应度函数评估个体适应度，以寻求在最合适各类传感器运行状态和配浆生产环境的模糊隶属度函数解作为最优个体，并将其标识为种群中的第n个个体，然后将该个体保留为下一代种群成员。
    (3)选择种群中所有个体(包括第n个个体)进行交叉操作。
　 (4)检查当前种群是否符合名义收敛条件，如果满足条件，则执行下一步，否则转向(1)。
　 (5)如果满足给定的优化条件，则终止优化过程，否则转向(1)。
3.2.2隶属度函数种群的编码表示
    本文选用如式(1)所示的梯形隶属度函数其描述，式中a、b、c、d是需要优化的参数。其中，b=c为三角形隶属函数，b=a为降半梯形函数，c=d为升半梯形函数，但是b=a和c=d不能同时发生。根据这些参数的不同，可以影响梯形函数的形状，产生不同的模糊集，从而对模糊推理的结果产生影响，使浓度控制算法具有较强的适应能力。隶属度函数的参数种群，采用实数编码方式,实数编码染色体表度比二进制编码的染色体长度短，编码方式简洁自然，减轻了遗传算法的计算负担，提高了运算效率，能够更好地保持种群的多样性。待编码的参数为a、b、c、d,每条染色体有4×n×m。其中n为输入变量的维数，m为混合料浓度模糊控制器中隶属度函数的个数(本文取3)。对于第一条染色体其编码如下：

3.2.3 适应度函数
    在算法进化中，个体适应度不仅需要考虑配浆浓度控制系统浓度跟随设定值的准确性，还需要考虑模糊推理系统本身的合理性和解释性。因此算法的适应度由两个部分组成，一是配浆浓度控制准确性指标，二是模糊隶属度函数的解释性指标。
    配浆浓度控制准确性指标即为模糊控制器输出的稀释水流量应使得浓度与浓度设定值间的偏差最小。因此，采用如式(5)所示的性能指标。

式中，Js(u)表示以模糊控制器输出的稀释水流量计算出的混合料浓度，J为浓度设定值。
    模糊隶属度函数的解释性指标：首先,考虑模糊隶属度隶属函数划分必须具有完备性，即保证隶属度函数能全部覆盖输入和输出变量的取值域，同时对于任何的输入变量，在其论域内的任何值，至少有一个隶属函数相对应，在形式上表现为隶属函数之间存在位置的交叉；其次,隶属函数划分必须是可区分的，即对于同一变量，隶属函数之间存在明显的位置区别，以便赋予一定的语义项。如果在寻优过程中，出现相邻的模糊集合的隶属度函数之间无重叠，就不能保证对于取值域内的任意输入都能找到一个模糊集合，即造成了隶属度函数的不完备性。另外还可能出现一个隶属度函数完全覆盖另外一个函数，这种情况的出现也会导致模糊推理系统本身不合理，并且不具有解释性。为了解决这些问题，相邻模糊集合的隶属度函数必须有一定的交叉率?琢。因此，模糊隶属度函数的解释性指标可表示为：

式(5)、式(6)的指标越小越好，采用分量加权求和，适应度函数为：

式中，加权因子v1、v2为正实数，预先根据经验设定，本文取v1=0.4，v2=0.6。
3.2.4 变异策略
    目前使用较多的变异策略有点式交叉变异和均匀交叉变异。点式交叉破坏模式的概率较小，但搜索到的模式较少；均匀交叉破坏模式的概率较大，但搜索到的模式较多。本文中解空间达到了4×n×m个维度，相对较大，采用点式交叉会使算法的收敛速度较快，因此本文采用点式交叉策略。
3.2.5 杂交策略
    目前使用较为广泛的杂交操作是单点杂交、两点杂交和多点杂交。采用单点杂交、两点杂交基因的变化较为缓慢，从而导致隶属度函数选择的周期增加，严重影响系统的整体效率，增加了配浆控制系统的滞后性。因此本文采用多点杂交的方式。
4 基于BP神经网络PID的内环控制器设计
    配浆浓度控制系统中，稀释水流量是调节配浆浓度的决定因素，但是稀释水阀门的开度-流量特性易受到水压、水量的干扰而常常发生变化。传统的PID控制方法，很难适应阀门的非线性特性，导致实际造纸流程中稀释水流量出现较大波动，精确度不高。神经网络具有任意非线性逼近能力、自学习能力以及概括推广能力，使系统具有自适应性[4-5]，可自动调节控制参数，提高控制性能和可靠性。因此本文将BP神经网络与PID控制方法相结合，用于控制算法来稀释水流量的调节。
4.1 算法结构
    本文所设计的基于神经网络PID的稀释水流量控制的结构如图3所示。控制器由两部分组成:传统的PID控制器和BP神经网络学习算法[6]。经典增量式PID的控制算法为：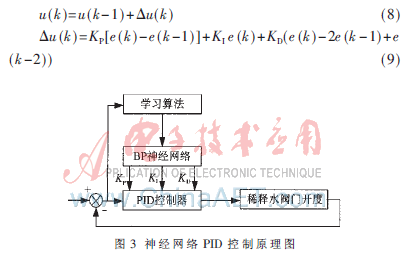

    神经网络根据配浆控制系统的运行情况，通过网络的自学习、权系数调整，使输出层神经元对应PID控制器的3个可调整参数比例(KP)、积分(KI)、微分(KD)，以使得配浆浓度控制系统能适应阀门的开度-流量特性，使稀释水流量跟随模糊控制器的输出值。
4.2 算法实现
    神经网络隐层层数是神经网络结构的重要参数，考虑系统本身复杂度、算法代价以及从实际应用效果，增加隐层后，稀释水流量控制精度提高并不明显。因此，本文采用一个隐层，与输入层和输出层共同构成三层BP神经网络，其结构如图4所示。

    按照梯度下降法修正网络的权系数，即按E(k)对加权系数的负梯度方向搜索调整，并附加一个使搜索快速收敛全局极小的惯性项，由此带来计算不精确的影响可以通过调整梯度下降法中的学习速度来补偿。由以上分析可得网络输出层权的学习算法为：

5 应用及结论
    将本文所提出的配浆控制方法应用于岳阳某造纸厂,该纸厂原采用PID控制实际数据曲线如图5所示，采用本方法控制系统实际数据曲线如图6所示。控制系统中浓度设定值为17.55%，经过分析比较，该厂原有控制算法控制偏差超过0.12%的时间占采样数据的60%，系统最大偏差为0.22%。而采用本文提出的控制算法，偏差超过0.07%的时间占采样数据的10%，其余数据均稳定在0.07%范围内，系统最大偏差为0.1%。从图中可以看出，本文算法利用模糊控制的优点来弥补配浆浓度控制中的突发干扰和利用遗传算法改善参数变化问题，同时利用神经网络PID算法自学习特点，自动调节控制参数，以适应配浆生产过程中的开度-流量非线性，使得浓度的控制精度得到了较大提高，完全能满足配浆过程浓度的工艺要求。

参考文献
[1] 于秀燕．自动配浆控制系统[J]．黑龙江造纸，2004(1):50-52.
[2] LIAN R J, LIN B F, HUANG J H. A grey prediction  fuzzy controller for constant cutting force in turning [J].
International Journal of Machine Tool and Manufacture, 2005, 45(9):1047-1056.
[3] 马清亮, 胡昌华, 杨青. 一种用于多目标优化的混合遗传算法[J]. 系统仿真学报, 2004,16(5):1038-1040.
[4] CHOY M C, SRINIVASAN D, CHEU R L. Neural network for continuous online learning and control [J]. IEEE Transaction on Neural Network, 2004,17(4):1511-1531.
[5] SBARBARO D, JOHANSEN T A. Analysis of artificial  neural network for pattern-based adaptive control[J]. IEEE  Transaction on Neural Network, 2006,17(5):1184-1193.
[6] 刘红波, 李少远, 柴天佑. 一种基于模糊切换的模糊负 荷控制器及其应用. 控制与决策[J]. 2003, 18(5): 615-
618.