FFT(快速傅里叶变换)在无线通信、语音识别、图像处理和频谱分析等领域有着广泛应用。在FFT运算中，核心操作是蝶形运算，而蝶形运算的主要操作是向量旋转，实现向量旋转可用复数乘法运算来实现，但复数乘耗费了FFT运算中大量的乘法器资源。CORDIC算法只需简单的移位与加减运算就能实现向量旋转，具有使用资源少、硬件规模小等优势。因此在FFT蝶形运算中用其代替传统FFT运算中的复数乘法器，可以获得更好的性能。但传统CORDIC算法中每次CORDIC迭代方向需由剩余角度的计算来确定，影响了工作速度。为此，本文根据定点FFT复乘中旋转因子的旋转方向可预先确定的特点，对CORDIC算法做了一些改进，在节省资源的同时保证了工作速度。
1 CORDIC算法原理
    假设直角坐标系中有一向量A(Xa，Ya)，逆时针旋转?兹角度后得到另一个向量B(Xb，Yb)，这个过程可用如下矩阵表示：
  
 

    针对这一特点，可在CORDIC算法上做一点改进，把旋转因子所对应的CORDIC旋转系数预先存在ROM中（人工计算旋转系数比较麻烦，可用MATLAB编一段程序来计算，并把旋转系数存为.mif文件以便ROM初始化），而不是把旋转因子角度预先存在ROM中。这样，在进行CORDIC运算时，直接从ROM中取出旋转系数，从而减少计算Zi来确定下一步旋转方向的步骤，减少CORDIC模块设计的复杂性，提高了运算速度，并且旋转系数不比旋转因子角度占用的ROM资源多。另外由于旋转因子需要进行0°、-90°或+90°三种预旋转，所以预旋转还要分配两位二进制数，这样存储旋转系数的ROM就为18位的ROM。
    改进的CORDIC算法结构如图1所示，所有旋转因子所对应的CORDIC旋转系数都存储在ROM中，通过地址产生器的控制实现序列与相应的旋转因子的复乘运算。与传统CORDIC算法相比去掉了预旋转角与已旋转角之差的计算来确定下一次旋转方向的结构，不但增加了系数寄存器模块，而且总体上结构更为简单。此CORDIC算法还采用流水线结构提高了运算的速度，从当前VLSI的发展趋势上来看，芯片内的门资源相对富裕，对流水线CORDIC的实现规模约束很小。此外，流水线CORDIC不存在迭代式CORDIC的反馈回路，使得单元结构更加规则，有利于VLSI实现。

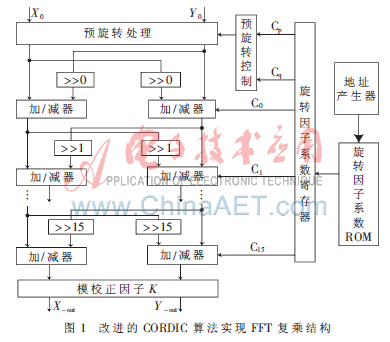
3.3 模校正因子的实现
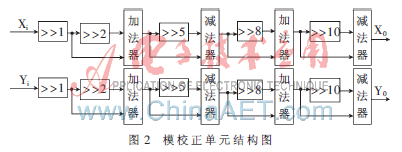
    基本CORDIC算法中在n级迭代执行之后，被旋转向量的模已经被改变了，算法的完全实现应该附加一个模校正环节，即Xn、Yn乘以模校正因子。对于迭代次数N大于10的CORDIC算法，其模校正因子可认为已趋近常数K=0.607 25。而直接在流水结构后附加乘法器的直接实现方法，使原本由移位器和加法器组成的整体结构变得不规则，同时乘法器一级速度的变慢会降低整个流水的吞吐率[3，4]。

这样分解后，被旋转向量与K的乘转化为简单的移位加减运算，从而可以解决乘法器一级速度变慢而降低整个流水线吞吐率的问题。其硬件实现结构如图2所示。这种结构进一步降低了硬件复杂度，与前面的流水线CORDIC结构相似，使整体结构更加规则统一，有利于VLSI实现。

4 FFT复乘的FPGA实现
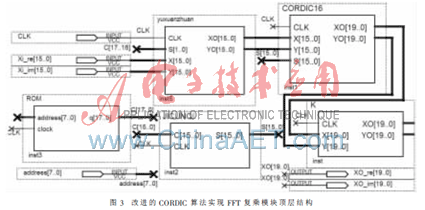
    由于软件和DSP实现的速度较慢，而FPGA资源丰富，组织结构便于采用流水线结构和并行运算，其速度快、扩展能力强，所以CORDIC算法的移位、加减法运算和流水线结构更容易在FPGA上实现。本文在Altera公司的QuartusⅡ7.2软件环境下使用VHDL，利用上述各种算法设计了16 bit宽的FFT复乘模块并在CycloneⅡ EP2C35F672C6芯片上进行验证。
    图3为改进的16级流水线结构的CORDIC算法实现复乘模块的顶层结构图，address为ROM的地址，Xi_re、Xi_im为输入序列的实部和虚部，Xo_re、Xo_im为旋转后的实部和虚部。输入数据为16 bit宽，为提高精度，对所有内部信号及输出信号都用20 bit的补码。整个复乘主要由系数ROM、预旋转、16级流水线CORDIC迭代、系数寄存器和模校正因子K 5个模块组成。

    小，但不能完全消除。

    图5为改进的CORDIC算法实现FFT复乘资源消耗与最高工作速度情况。传统的复乘要4个乘法器，所以传统的复乘要实现16 bit位宽复乘需用此芯片中的8个9 bit乘法单元，而从资源消耗情况来看，改进的CORDIC算法实现此复乘没有用乘法器，整个逻辑单元消耗也只有4%；另外基于改进的CORDIC算法的复乘最高工作频率达到了190 MHz，与传统CORDIC算法的复乘速度（约130 MHz）相比有较大提高，在节约资源的同时提高了工作速度。

    本文利用定点FFT复乘运算中旋转因子的旋转系数可预先求出的特点，采用改进流水线结构的CORDIC算法，与传统的CORDIC算法的复乘相比，不仅不需要乘法器实现了FFT运算中序列与旋转因子的复数乘运算，并且在节约资源的同时提升了工作速度。这种基于改进的CORDIC算法的复乘运算对提高FFT处理器的速度和减少资源消耗有较大意义。同时，利用VHDL语言，采用模块化设计思想，使得本设计可移植性强、通用性好，只需作少量改动（如增加位宽，增加迭代次数），便可满足精度上的更高要求，具有一定的工程实际意义和应用前景。
参考文献
[1] 李成诗，初建朋.基于CORDIC的一种高速实时定点FFT的FPGA实现[J].微电子学与计算机，2004，21(4).
[2] 吴伟，唐斌.现代雷达中的高速FFT设计[J].空军工程大学学报（自然科学版），2005(10).
[3] KHARRAT M W，LOULOU M，MASMOUDI N，et al.A new method to implement CORDIC algorithm[C].IEEE International Conference on Electronic，Circuit and Systems，2001(2)：715-718.
[4] 杨宇，毛志刚，来逢昌.一种改进的流水线CORDIC算法结构[J].微处理机，2006(8).
[5] 李滔.流水线CORDIC算法及其应用研究[D].北京理工大学，1999.