摘 要: 针对序列模式的几个经典的算法的缺点,提出了一种基于时间约束序列模式的快速产生候选项的方法(TFEGC)。此算法不但避免了频繁的扫描数据库,还考虑了时间限制因素,避免了无用的候选序列的产生,提高了算法运行的时间效率。
关键词: 序列模式挖掘;时间约束;候选项;快速产生
序列模式挖掘在很多领域都具有十分重要的意义,比如它可以根据分析顾客购买行为来决定商品的摆放位置,从而制定商场的营销策划。所以,近年来出现了很多序列模式挖掘的改进算法,目前提出算法中,有两类比较典型:GSP[1]算法和采用分治策略来进行模式增长的PrefixSpan[2]算法。但是这两种算法都存在一定的缺点。参考文献[3]中提出的快速有效的产生候选项的FEGC算法,不需要多次扫描数据库,且不需要在前一次迭代的基础上来产生候选项,也不需对非频繁项进行剪枝或修剪,能够达到快速产生候选项的效果。但是,FEGC算法是针对数据库总体的序列来产生候选项的,有些并不是有效的和用户感兴趣的序列,这在实际应用中就耗费了大量的时间和空间,如分析顾客的购买行为,就不需要将其一月份购买的产品和十二月份购买的产品放在一起进行研究比较。所以本文在FEGC算法的基础上将时间限制因素加了进去,可称之为TFEGC算法,本算法继承了FEGC算法的优点,而且避免了不必要的、无用的一些候选项的产生,提高了算法的运行效率,且在序列结合的过程中,只需检查uid、fid(t)以及s(t)的值,便可知道与哪些项进行结合,无须再进行检验。
1 相关算法介绍
GSP算法,即广义序列模式算法,使用序列模式的向下封闭性,并采用多次扫描的候选产生-测试方法,它是由Srikant和Agrawal于1996年提出的。它的主要思想是利用序列模式的种子集,即前次扫描得来的序列模式来产生潜在的频繁序列,即候选序列,每个候选序列都会比产生它的种子序列模式多包含一个项。直到一遍扫描不能产生新的序列模式或者新的候选序列时,算法终止。
PrefixSpan算法是前缀投影序列模式增长算法[4],此算法的特点是不需要产生候选项,算法思想是先找出各个频繁项,然后分别产生它们所对应的投影数据库,接着对各个投影数据库进行挖掘,最后将前缀模式与后缀模式相连得到频繁序列。此算法的缺点就在于可能会产生大量的投影数据库,而且要扫描数据库多次[3]。
FEGC算法的特点有:(1)Head、Body、Tail的引入,在一个交易序列中,处于Head的项在形成二序列时,只能作为二序列中的Head,处于Body的项在形成二序列时,既可以作为Head,也可以作为Tail;(2)Nid的引入,Nid的作用是用来规定在形成候选序列的过程中的2-序列的结合顺序[1]。
2 TFEGC算法的理论和相关概念
对于给定的某个顾客的交易数据序列B={(Item,TID),…},其中Item表示交易的项,TID表示交易的时间,设I={(i1,t1),(i2,t2),…(in,tn)}是由n个不同的项组成的序列,它记录了某个顾客在不同的时间购买的产品,然后根据时间限制将这个序列划分成不同的子序列,再将这些子序列转化为2-序列[5],最后以这些2-序列为基础,找出所有的候选项。

2.2 公式的应用及td的引入
上面的三个公式都是为了解决利用TFEGC算法来求候选项时遇到的问题,它们所发挥的作用可通过下面的具体例子来进行详细描述。
由图1可知所有的2-序列过程,下面以子序列<bcde>产生的2-序列<bc>为例,具体过程如下:
(1)计算出uid=4-2=2,fid(c)=4-2=2,fid(d)=4-3=1,s(c)=2-1=1,s(d)=3-1=2;
(2)对于2-序列<bc>,因为s(c)=1,说明它只能与排在子序列<bcde>之后的第一个子序列产生的2-序列相结合,由图1可知是子序列<cdef>产生的2-序列;又因为fid(c)=2,说明它只能与<cdef>产生的前两个2-序列<cd>、<ce>相结合,生成<bcd>、<bce>;又因为s(d)=2、fid(d)=1,说明<bcd>还可以与排在子序列<bcde>之后的第二个子序列<def>产生的第一个2-序列<de>进行结合,生成<bcde>,e为子序列<bcde>的最后一项,不作考虑。

由上面的步骤(2)可知,虽然求得了s(c)的值,但是在算法的实现过程中,并不知道子序列<cdef>就是排在子序列<bcde>之后的第一个子序列,为了解决这个问题,引入了td的值,为节省存储空间,可以用矩阵的形式来存储td的值,如图2所示。
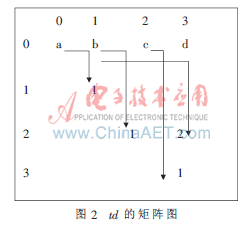
矩阵中没有出现项e和项f,因为项f为序列的最后一项,所以它不会与任何二序列进行结合,由图1知并没有产生以e为首项的子序列,所以不会产生以e为首项的2-序列。
其中,[1,1]=1-0=1,表示排在以a为首字母的子序列之后的第一个子序列,是以b为首字母的子序列;[2,2]=2-1=1,表示排在以b为首字母的子序列之后的第一个序列,是以c为首字母的子序列,依此类推。
所以,当算出s(t)的值时,只需比较其与td的值,当s(t)=td的值时,则此序列就是所要结合的2-序列。
3 TFEGC算法
3.1 算法思想
本算法一共有四大步,第一步是根据时间限制将原序列划分为多个子序列;第二步是将得到的子序列转化为2-序列;第三步是根据uid、fid(t)和s(t)的值将2-序列进行结合,从而得到所有的候选项;第四步根据最小支持度minsup得到频繁项集。
从上所述可以看出,此算法的主要特点有:(1)加入了时间限制因素;(2)只需要扫描数据库一次,节省了算法的运行时间;(3)引入了uid、fid(t)、s(t),使之在形成n-序列的过程中,能够准确地找到要结合的2-序列,不需要扫描所有子序列产生的二序列,提高了算法的时间效率。
3.2 TFEGC核心算法描述
2-序列结合的算法如下:
for all I∈DB{ //I为满足时间限制的子序列
l=strlen(I);
uid=l-2;
for(n is smaller thanl ){
if(in∈I and n≠1 and n≠1)
{ //in不能为首尾两项
s(in)=n-1;
fid(in)=l-n;}
}
for(scan the Matrix Chart of td){//扫描矩阵td
if(td==s(in)){
record the item r and
record those 2-sequence se whose first item is r;}
//r用来存放首项,se用来
//存放以其为首项形成的2-序列
}
for all tn∈se{
if(tn.index==fid(in)){//找到所要结合的2-序列
in+tn;}//2-序列in和2-序列tn相结合
}
}
3.3 算法举例
为了进一步描述TFEGC算法,以图1中的子序列<abc>产生的第一个2-序列<ab>为例,求以这个2-序列为基础所形成的候选项过程,如图3所示。

4 实验结果
算法实验环境为PentiumⅣ3.0 GHz双核 PC机器,内存为1 GB,Windows XP操作系统,采用C++语言在VC编程环境下实现。实验测试数据采用IBM数据生成器,该生成器是目前数据挖掘相关研究中使用广泛和权威的生成器,可以通过设置参数生成不同特性的数据集,具体参数含义如表1所示。
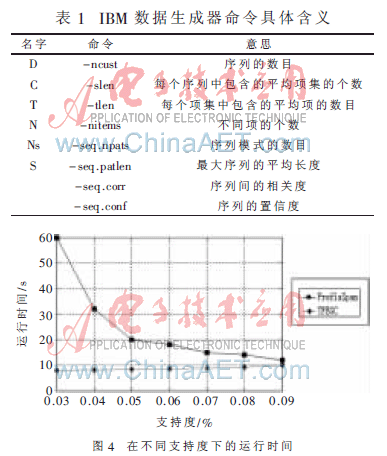
PrefixSpan算法和TFEGC算法在不同的支持度下的运行时间如图4所示,从结果可以看出文中提出的方法优于PrefixSpan算法,因为TFEGC算法只需要扫描数据库一次,而且由于uid、fid(t)以及s(t)的引入,避免了一些无用序列的产生,大大减少了运行时间。
图5所示的是FEGC和TFEGC在不同数量的顾客下算法的运行时间,从中也可以看出TFEGC算法的运行时间少于FEGC算法的运行时间。这是因为在二序列的结合过程中,TFEGC不需要逐个扫描其他的二序列,只需查看uid、fid(t)以及s(t)的值就可以判断应该与哪些二序列进行结合,而且生成的用户不感兴趣的序列也大大减少了。因为加入了时间的限制,所以根据支持度来提取频繁序列的时间也就相应地减少了。

本文提出的算法,可由用户自己设定时间限制来查找频繁序列,也可以用来处理不同数量的客户群,所以具有一定的灵活性。又因为其只扫描数据库一次,而且二序列的结合也具有一定的明确性,所以在时间效率上具有一定的优越性[6]。
参考文献
[1] SRIKANT R,AGRAWAL R.Mining sequential patterns:generalizations and performance improvements[C].Proc.of Int’l Conf.on Extending Database Technology,1996:3-17.
[2] PEI J,HAN J,Mortazavi-Asl B,et al.Prefixspan: mining sequential patterns efficiently by prefix-projected pattern growth[C].Proc.of Int.Conf.on Data Eng. (ICDE’01),2001:215-224.
[3] Liao Weicheng,Yang Donlin,Wu Jungpin,et al.Fast and effective generation of candidate-sequences for sequential pattern mining[C].2009 Fifth International Joint Conference on INC,IMS and IDC,2009:2006-2009.
[4] 赵畅,杨冬青,唐世渭.Web日志序列模式挖掘[J].计算机应用,2000,9(20):13-16.
[5] 连一峰,戴英侠,王航.基于模式挖掘的用户行为异常检测[J].计算机学报,2002,25(3):325-329.
[6] 吉根林,帅克,孙志挥.数据挖掘技术及其应用[J].南京师范大学学报(自然科学版),2000,23(2):25-27.

