文献标识码: A
文章编号: 0258-7998(2011)07-153-03
模乘运算在公钥密码系统中(例如RSA算法、椭圆曲线密码算法(ECC)以及ElGamal算法等)有着广泛的应用。Montgomery模乘算法利用易于硬件实现的加法和移位操作来实现大整数的模乘运算,避免了复杂的除法运算,从而大大提高了模乘运算的效率[1]。
本文提出一种高速可扩展的Montgomery乘法器设计方案,该方案是在Tenca提出的Booth-8 Montgomery模乘法器的基础上,采用Booth-64编码进行改进,使速度平均提高了48%。同时对数据通路进行了优化,使得流水线数据通路的平均延迟大大降低。
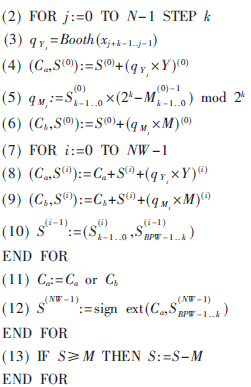
其中,k表示基,X为模乘运算的乘数,Y是被乘数,M是模数。其中,操作数长度为N,部分积用为S表示,Y、M和S分成NW个BPW bit的字进行运算,xj表示X的第j bit,Sk(i)表示第i个字的第k位,Ca、Cb表示进位,qyj、qMj分别是在计算部分积过程中Y和M的系数。
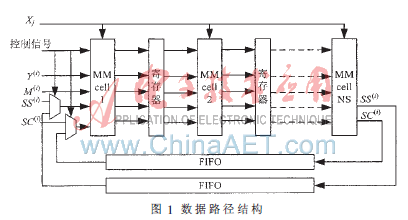
核心数据路径采用流水线组织结构,每一级之间用寄存器隔开。每个MMcell单元完成一轮外循环,每个时钟输入Y、M、SS、SC的一个字参与运算,并把Y、M和计算出来的SS、SC传递该下一级。为了能使数据路径可伸缩,加入了两个FIFO分别用来存储SS和SC。如图1所示,NS是流水线级数,由面积和时间需求来决定。
2 基为64的高速Montgomery乘法器设计
Tenca提出的模乘器设计中Booth编码采用的基为8,并且能够支持操作数长度可变的模乘运算,对操作数按字进行运算,缩短了关键路径的延迟,并且使用CSA(Carry Save Adder)提高了整体的系统性能。
通过分析,采用基为8的Booth编码可以将部分积数量减少为原来的1/3,而采用基为64的Booth编码则可以将部分积数量减少为原来的1/6。据此本文对Tenca提出的设计方案进行改进,因此提出基为64的高速Montgomery乘法器。
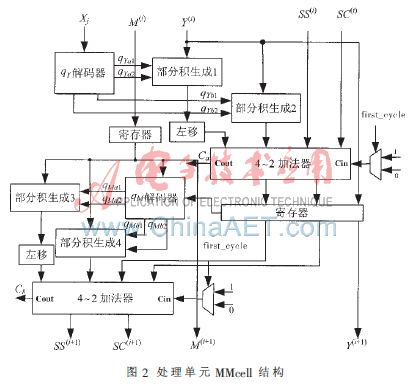
对于基为64的设计,乘数X每次扫描6 bit,经Booth编码后得到7 bit的输入数据,同时Y和M每次输入一个字。乘数X的Booth编码为:

3 性能分析与比较
对于基为64的Montgomery乘法器,计算一次模乘运算的总时钟周期数时,需要考虑NW≤2NS和NW>2NS两种情况,NW代表操作数所含的字数。一个MMcell需要两个时钟周期的执行时间,因此一个字经过流水线的总时钟周期数是2NS+1。由于每次可处理6 bit,所以需
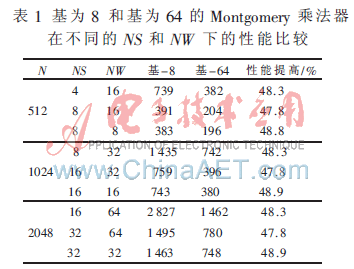
从表1可以看出,在不同条件下,本文的设计在性能上平均比Tenca的设计提高了48%。本文采用字长32 bit,级数NS=8实现基为64的Montgomery乘法器,且使用Verilog HDL语言实现上述设计,并使用ModelSim 对设计进行了仿真验证;基于SMIC 0.18 μm CMOS标准数字逻辑工艺,利用Design Compiler 进行了综合设计,结果显示频率达到251 MHz,面积为37 381门。
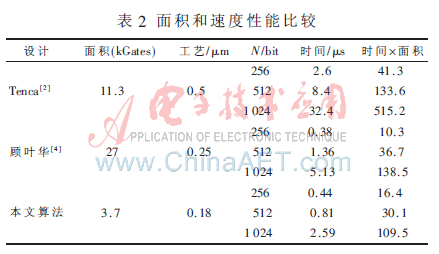
顾叶华在参考文献[4]中对Tenca提出的流水线结构进行了优化,提出了一种基为4的Montgomery乘法器方案。面积和速度的比较如表2所示。从表中可以看出,本设计在512 bit和1 024 bit下具有最小的时间×面积的值,综合性能最优。
本文对Tenca提出的基为8的可扩展Montgomery模乘器进行改进,采用了更高的基为64的设计,进一步减少了部分积的个数,缩短了运算时间。与Tenca在参考文献[2]中的设计相比,时钟周期数平均减少了48%,并且缩短了关键路径的延迟相比,综合性能具有明显地提高。
参考文献
[1] KOC C K, ACAR T, KALISKI B. Analyzing and comparing Montgomery multiplication algorithms[C]. IEEE Micro, 1996:26-33.
[2] TENCA A F, TODOROV G,KOC C K. High-radix design of a scalable modular multiplier[A]. Cryptography Hardware and Embedded System-CHES 2001. Springer Verlag, Berlin, Germany, 2001:189-205.
[3] 颜晓东,李树国. 二次Booth编码的大数乘法器设计[J].清华大学学报(自然科学版),2007,47(10):1681-1684.
[4] 顾叶华,曾晓洋,赵佳,等. 一种新型操作数长度可伸缩的模乘器VLSI设计[J]. 计算机工程, 2007,33(19):227-229.

