摘  要： 空间索引作为空间数据库的关键技术，其性能的高低决定着整个空间数据库的效率。通过对现有的多种空间索引结构进行比较分析，基于开源数据库Ingres实现了广度优先R树连接算法(BFRJ)，并对其进行了局部优化和全局优化。基于真实数据的实验结果分析，证实了采用适当的全局优化方法的BFRJ优于其他已知的空间连接算法方法。
关键词： 空间索引；空间连接；Hilbert R树；BFRJ

　常见的空间查询有点查询、窗口查询(或称范围查询)、相交查询(或称区域查询)、被包围查询、毗连查询、最近邻查询、空间连接查询等，其中空间连接查询是最重要、最耗时的空间查询[1]。本文首先对Ingres原有空间连接方式进行研究。然后参照已有的相关研究论文，采用基于宽度优先的R树空间连接算法，并对其进行全面测试(包括功能和性能测试)，并与Ingres原有空间连接进行性能对比。
1 Ingres空间连接算法
　Ingres原有的空间连接执行时，如果两个表都建有R树索引，其QEP为TID Join。如有两个表RTreeJoin1和RTreeJoin2，对应的空间索引为RTree1和RTree2，如果执行Select*from RTreeJoin1，RTreeJoin2 where RTreeJoin1.obj overlaps RTreeJoin2.obj，QEP如图1所示。

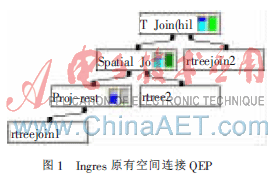
　图中Spatial Join即Key Join，首先是将RTreeJoin1.obj的值作为键值查找索引RTree2，所得对应RTreeJoin2中的TID，然后再以此TID直接访问RTreeJoin2中的元组，即TID Join。此种方式没有利用两个基表都建有RTree的优势，因此在部分情况下不能获得最优的性能。这种方法称为“One-Rtree-Only”空间连接方法[2]。
2 Ingres空间连接算法改进
　针对上述分析，希望能够在过滤阶段即利用两个R树索引。通过对两个索引进行按深度或按宽度的遍历，执行过滤运算，不可能满足连接条件的空间对象迅速排除[3-4]。本文将参考文献[5]使用广度优先遍历算法优化R树空间连接。
2.1 在遍历R树时剪枝
　在R树中维护的一个重要信息就是它的层次性蕴含着它的包含性。即一个树结点的MBR总是包围着它的子孙结点的MBR。利用这一特点可知，一对结点nRir和nSjS需要进行连接仅当它们父结点的MBR相交，称为剪枝。简单的从顶至底的图遍历算法可以在任何层次上使用这种剪枝。参考文献[5]中剪枝是在同时深度优先遍历两棵输入的R树时进行的(DFRJ)，而参考文献[6]则是在同时广度优先遍历两棵R树时进行的(BFRJ)。在R树的所有层次施行剪枝达到的效果是从顶层起，分别来自两棵R树的两个结点被遍历到仅当它们父结点的MBR相交。这样，相比简单的嵌套循环的遍历方式，剪枝将使得被遍历的不相交的结点对数大大减少。
2.2 BFRJ算法
　基于广度优先遍历的R树空间连接算法(BFRJ)步骤为：(1)对两棵R树的根结点(NR，NS)做一次结点连接。所谓结点连接，就是对输入的两个非叶子结点，返回其相交的元素项对。对根结点做结点连接的结果是一个二元组(oidR0，oidS0)的集合，称为0阶中间连接索引IJI0(intermediate join index at level 0)。因为本文主要着眼于对相交运算的空间连接，因此每一个二元组(oidR0，oidS0)意味着这两个元素项的MBR相交。(2)对于IJI0的每一个二元组，BFRJ找出其在两棵R树中对应的结点，进行结点连接。当BFRJ从IJI0中读入一个二元组进行计算时，它会以二元组(oidR1，oidS1)的形式保存结果，加入当前的1阶中间连接索引IJI1。当BFRJ处理完IJI0中的所有二元组后，它会释放IJI0并开始对IJI1进行相应的连接操作。这个过程随着BFRJ算法逐层遍历R树而继续着。当中间连接索引由两棵R树的叶子结点产生时，算法终止。如果两棵R树不等高，算法将在到达一棵树的叶子结点(如R)时，枚举叶子结点中的每一个元素项对另一棵树S中对应子树做查询操作。到此，空间连接过滤环节已经结束，当前的(叶子级的)IJI已经不在空间连接的范畴之内了。

2.3 局部优化技术
　局部优化技术是在结点连接的过程中进行的。在参考文献[6]中介绍了两种局部优化技术，分别为搜索空间限制(Search Space Restriction)和平面扫描(Plane Sweep)。
2.3.1 搜索空间限制
　在一对结点nRir和nSjS进行连接时，它们的MBR的交叉区域仍然是MBR(称为intersect-MBR)。如果nRir中的元素项(oidRir，mrbRir)x同nSjS中的元素项(oidSjS，mrbSjS)y相交，则mrbRir和mrbSjS必须同两个结点的intersect-MBR相交。因此，可以首先对nRir和nSjS的元素项分别进行扫描，排除掉那些MBR同intersect-MBR不相交的元素项。在进行结点连接时，仅对剩余项进行连接。
2.3.2 平面扫描
　这一优化方式同合并两个普通的数据集合时采用的排序-归并技术类似。在一对结点nRir和nSjS进行连接的过程中，首先分别对两个结点中的元素项依MBR进行排序。为了对多维数据进行排序，用MBR的最小x值作为关键字。在合并阶段，依次对排序的MBR进行扫描。对于一棵树中的MBR，仅对于其x坐标相交的MBR进行相交测试。
　这两种优化技术各有侧重，搜索空间限制技术可以对于结点容量较大但元素项分散的数据进行较大优化，而平面扫描对于多维数据的优势更大。
2.4 全局优化技术
　在BFRJ算法框架下，i阶中间连接索引(IJIi)在两棵树中所有的i层结点连接完毕后产生。而在i层进行结点连接的结点对来自于由更高的(i-1层)结点连接产生。因此可以在对一层结点进行结点连接之前，获取该层所有结点访问预计(包括它们可能的访问顺序和重复访问次数)的全局信息，可以利用一些技术来对中间连接索引进行高效的管理。
2.4.1 中间连接索引排序
　设结点的MBR同R树S的k个t级结点的MBR相交，则nRit的索引ID在IJIt-1中出现了k次。在计算t层的结点连接时，nRit将被恰好计算k次。对于一个固定大小的LRU系统缓冲，如果ID在IJIt-1中出现的比较分散，则结点nRit将从硬盘中被多次读取(最多k次)。这是因为第一次和后面出现的对nRit的调用之间可能会比较远，在需要被再次读入时可能已经从缓冲区中删除。因此希望IJI能够维护在一种有序的状态下，使得多次出现的相同结点的ID在IJI中出现的位置不要分散得太过稀疏。
2.4.2 中间连接索引内存管理
　IJI可以被存储在内存中或是磁盘上。前者能提高IJI排序的效率并减少读取IJI时多余的I/O操作；而后者能解放出更多的内存资源用于连接计算。
2.4.3 中间连接索引缓冲管理
　IJI排序技术倾向于维护索引的顺序，使得任意两个相同ID出现的位置不会相隔太远。然而，对两个项目都实现很好的聚类效果是不可能的，在连接运算中，对一个结点的多次磁盘读取依然存在。如果缓冲管理可以预测哪个结点已经连接完毕，而哪个结点将来还会参与运算，则这种多次读取可以被进一步缩减。用这种方式，缓冲管理可以保留那些将来还会参与运算的结点页面，而将已经结束所有连接运算的结点页面清理释放。
3 实验结果
　采用实际数据进行实验。实验数据来自www.rtreeportal.org的两个数据组：
　(1)“Germany”数据组，包含四个数据包：
　①“roads”：包含了德国的30 674条街道的MBR；
　②“rrlines”：包含了36 334条铁路线的MBR；
　③“utility”：包含了17 790条公用网络的MBR；
　④“hypsogr”：地势图，由76 999个MBR组成。
　(2)“Greece”数据组，包含两个数据包：
　①“roads”：包含了希腊的23 268条街道的MBR；
　②“rivers”：包含了24 650条河流的MBR。
　将这些数据包组成四个连接对进行实验，即“Germany：roads，rrlines”，“Germany：roads，utility”，“Germany：roads，hypsogr”，“Greece：roads，rivers”。
在实验中，固定了R树的页面大小，这样，影响连接性能的主要参数除了使用的方法外即为缓冲大小。用缓冲区最多存放R树页面的个数作为衡量缓冲大小的参数，这样在不失一般性的同时可以简化缓冲管理操作在程序内实现。
　表1~表4给出了连接对“Germany：roads，rrlines”的实验结果，其中的数据表示在给定的缓冲大小下给定空间连接方法在给定缓冲大小下对应的页面I/O次数m。

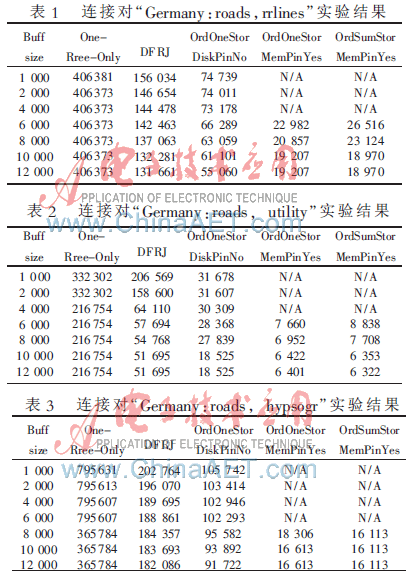
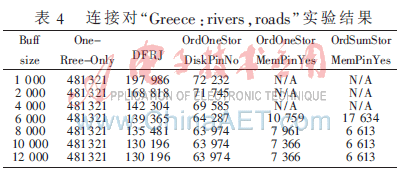
　从实验结果分析各连接方法，Buff size表示缓冲区大小，One-Rree-Only表示只对一个数据包建R树；DFRJ表示使用DFRJ方法进行R树连接；OrdOneStorDiskPinNo表示采用基于磁盘存储的非特定排序优化组合BFRJ方法进行空间连接；OrdOneStorMemPinYes表示采用基于主存存储的对单棵树排序优化组合BFRJ方法进行空间连接，OrdSumStorMemPinYes表示采用基于主存存储的对中值和排序的优化组合BFRJ方法进行空间连接。由于StorMem意味着要将IJI保存在主存中，因此对缓冲大小有要求，当缓冲较小时则不适用，对应的表格项为N/A。
　在真实数据的条件下，对于任意的缓冲大小，基于两棵R树的空间连接算法(DFRJ和BFRJ)的性能总是优于基于一棵R树的算法(One-Rree-Only)。而在R树空间连接方法中，使用适当全局优化组合的BFRJ又明显优于DFRJ。在缓冲较小时，OrdOneStorDiskPinNo最适用；在适中的缓冲条件下，StorDisk的性能要比StorMem差，OrdOneStorMemPinYes相对更优；而在较大的缓冲条件下，OrdSumStorMemPinYes能够获得最好的空间连接性能。
参考文献
[1] KAMEL I， FALOUTSOS C. Hilbert R-tree： An improved R-tree using fractals[M]. In： Proceedings of the 20th VLDB， Santiago， Chile， 1994，500-509.
[2] HUANG P W， LIN P L， LIN H Y. Optimizing storage utilization in R-tree dynamic index structure for spatial databases[J]. Journal of Systems and Software， 2001，55(3)：291-299.
[3] BRAKATSOULAS S， PFOSER D， THEODORIDIS Y. Revisiting R-tree construction principles[M]. In： Proceedings of the 6th ADBIS， Bratislava， Slovakia， 2002，149-162.
[4] BRINKHOFF T， KRIEGEL H. P， SEEGER B. Efficient processing of spatial joins using R-trees[M]. In： Proceedings of ACM SIGMOD， Washington DC， 1993，237-246.
[5] MARTYNOV M. Spatial joins and R-trees. In： Proceedings of the 3rd ADBIS[M]， Moscow， Russia， 1995，295-304.
[6] HUANG Y W， JING N， RUNDENSTEINER E. Spatial joins using R-trees： Breadth First traversal with global optimizations. In： Proceedings of the 23rd VLDB， At hens， Greece， 1997，396-405.