摘 要：在分析和研究电力线路最佳抢修路径的基础上，提出了一种改进的遗传禁忌搜索算法来求解电力线路最佳抢修路径。此算法基于变异思想和A^*算法产生禁忌搜索算法的邻域解，并利用遗传算法的阶段进化思想减少调用禁忌搜索算法的频率,进而提高改进的遗传禁忌算法的执行效率。仿真结果表明在求解电力线路最佳抢修路径时，遗传禁忌搜索算法的性能优于其他算法。
　　关键词：遗传算法；禁忌搜索；最佳抢修路径；A^*

　　随着生活水平的提高，电力系统的发展，电力线路逐渐增多，线路故障时有发生。突如其来的自然灾害更易造成大面积的杆塔和线路故障，抢修不及时将严重影响生产、生活。因此，电力线路最佳抢修路径的研究就成为当今的一个热点问题^[1]。
　　电力线路最佳抢修路径问题就是在检测到故障地点后，派遣抢修人员及时地到达故障现场，减少故障造成的破坏。现在已经有很多算法来解决此问题，如Dijkstra、模拟退火算法、蚁群算法、遗传算法。但是随着网络规模的逐渐扩大，Dijkstra算法内部的二重循环将使其执行效率严重下降。模拟退火算法虽然能找到最优解，但是冷却参数的设置很难把握^[1]。蚁群算法虽然具有很强的实用性，但易于陷入局部最优解且收敛速度慢。
　　传统的遗传算法具有很强的鲁棒性，适合于求解电力线路最佳抢修路径，但是具有较差的局部寻优能力^[2]。然而，禁忌搜索算法具有较强的局部搜索能力^[3]。本文结合两者的优点，利用遗传禁忌搜索算法来求解电力线路最佳抢修路径；同时结合A*算法^[4]和变异思想^[1]，提出了一种禁忌搜索算法邻域解产生的新方法，并利用遗传算法阶段进化思想，减少调用禁忌搜索算法的频率，进而提高遗传禁忌搜索算法的执行效率。
1 电力线路最佳抢修路径的数学模型
　　电力线路最佳抢修路径就是交通网络中抢修人员从物资点到故障点花费时间最少的路径。所以，需要先找到故障点邻近的路段交叉口(目的节点T)和物资点邻近的路段交叉口(起始节点S)，然后在交通网络拓扑图中求取S到T的耗费时间最短的路径。因此，把交通网络中的路段抽象为平面图中的边，把路段交叉口抽象为平面图中的顶点，形成一个平面图G(V,E)，其中V为顶点集合，E是边的集合，如果顶点i到顶点j有直接相连的边，则X_ij=1，否则Xij=0。Wij是边(i,j)的权重，即通过路段i→j所花费的时间。最佳抢修路径就是从S到T的一些中间节点的集合(a₀(S),a₁,a₂,…,a_i ,…,a_n(T))。因此电力线路最佳抢修路径的数学模型为：
　　　　

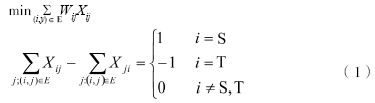
　　受到路段行驶速度、交叉路口的延误、交通管制等交通因素的影响，路段i→j的权重Wij由行驶时间和交叉路口的延误时间两部分组成。本文将路段允许平均行驶速度划分为8个等级^[5]。行驶时间tij为路段的长度d_ij除以行驶速度v_ij，即t_ij=d_ij/v_ij。利用道路等级来确定各交叉口的平均延误时间t_i，每条路段均有两个交叉口，则路段i→j的交叉口延误时间为(t_i+t_j)/2，故W_ij=t_ij+(t_i+t_j)/2^[1]。
2 遗传禁忌搜索算法的改进
　　GA和TS算法分别具有各自独特的优点并存在着无法避免的缺点。若能将两者混合起来使用，则能发挥两者优势，有效提高求解质量和均衡算法的运行效率。本文综合分析了遗传算法和禁忌搜索算法，提出了一种改进的遗传禁忌搜索算法来求解电力线路最佳抢修路径，即利用遗传算法产生初始群体，经过选择、交叉、变异操作后，在合适的时机调用禁忌搜索算法来对每个个体进行局部搜索。根据电力线路最佳抢修路径的特点，此算法的改进主要集中在以下两点：一方面针对遗传算法频繁调用禁忌搜索算法造成时间复杂度大幅度提高的问题，提出了减少禁忌搜索算法调用频率的新策略；另一方面针对遗传算法在求解最佳抢修路径时，产生的每个个体的染色体长度是不同的，提出了禁忌搜索算法邻域解产生的新方法。
2.1 禁忌搜索算法的调用时机
　　虽然遗传算法和禁忌搜索算法的结合，使得禁忌搜索算法的强爬山能力弥补了遗传算法较差的局部搜索能力，但是也存在一些问题。其中最主要的是算法的执行效率问题。遗传算法频繁调用禁忌搜索算法，显然大大地增加了算法的计算复杂度，不利于大规模问题的求解。故本文按照遗传算法阶段进化的思想，确定禁忌搜索算法的调用时机，进而减少禁忌搜索算法的调用频率。
　　遗传算法进化初期属于探索阶段，必须充分利用交叉算子探索基因空间的能力，在较大的解空间中搜索全局最优解或其邻域。此时，可以不调用或者以较小的概率调用禁忌搜索算法。随着个体的逐渐进化，交叉操作的概率性和随机性使得群体中的染色体具有局部相似性，这时可适当提高禁忌搜索算法的调用概率。在遗传算法的进化后期，群体转向局部搜索的过程。此阶段侧重个体的局部搜索。由于遗传算法的局部搜索能力差，这时可以较大概率地调用禁忌搜索算法。经过以上分析，本文将遗传算法的进化过程划分为三个阶段^[2]。三个阶段划分如下：第一阶段[0,T₁]，第二阶段[T₁, T₂]，第三阶段[T₂, T_g]。其中
　　
2.2 邻域解的产生
　　对于禁忌搜索来说，邻域结构的设计是非常重要的。不同的邻域结构将导致邻域解的个数及其变化情况不同，对搜索质量和效率有一定的影响，但目前尚无一般定论。再者在电力线路最佳抢修路径的求解过程中，遗传算法产生的每个个体代表一条物资点到故障点的抢修路径，是一些中间节点的集合。因此，本文利用A^*来产生当前解的邻域解。同时，为解决过多调用A*算法带来的算法复杂度大幅度提高问题，在邻域解的产生过程中引入了变异思想。
　　

3 算法实现
　　在求解电力线路最佳抢修路径问题时，本文提出的改进的遗传禁忌算法的步骤如图1所示。首先，在抽取出的交通网络拓扑图上，规定初始节点S和目标节点T；然后利用GA产生一些初始路径，进而通过选择、交叉、变异操作产生下一代种群；最后，判断遗传算法的当前迭代次数是否满足调用禁忌搜索算法的时机。若满足，则调用禁忌搜索算法对新一代种群中的每个个体进行局部搜索，接着进行GA的下一次迭代。若不满足，则直接进入遗传算法的下一次迭代。重复上述步骤，当满足终止准则时，则结束迭代过程并输出最优解。总之，利用改进的遗传禁忌搜索算法求解电力线路最佳抢修路经的主要步骤是：染色体编码、适应值函数、初始种群的产生、选择算子、交叉算子、变异算子、局部搜索和终止准则。
3.1 染色体编码
    在本文中，染色体的编码采用字符编码代替传统的二进制编码和实数编码。它是从初始节点到目标节点的一系列中间节点的集合。再者，由于电力线路最佳抢修路径是一系列中间节点的集合，所以每个个体的编码长度是不同的。
3.2 适应值函数
    对电力线路最佳抢修路径的研究就是要找到一条物资点到故障点耗费时间最少的路径。按照上文提到的路段权重的确定方法，任一个体(a0(S),a₁,…,a_i ,…,a_n(T))的适应值函数为：
　　
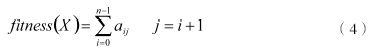
3.3 初始群体的产生
　　每一代的个体之间总是有联系的，否则进化过程将变得没有意义。本文采用下面的步骤产生初始种群：
　　（1） 把初始节点作为第一个节点。
　　（2） 从它的子节点中随机地选取一个节点作为当前节点。
　　（3） 如果当前节点不是目标节点转步骤（2）；否则继续。
　　（4） 如果当前节点是目的节点，则终止搜索过程，若此个体含有环路，则消除个体中的最大环，进而产生一个个体。
　　（5） 重复上述步骤，直到产生所有的个体。
3.4 选择算子
　　本文中选择了轮盘赌选择算子。
　　选择即从当前种群中选择适应值高的个体以生成交配池的过程。轮盘赌选择算子是最基本的选择方法，其中每个个体被选择的期望数量与其适应值和群体平均适应值的比例有关。轮盘赌选择算子首先计算每个个体的适应值，然后计算出适应值在群体适应值总和中所占的比例,表示该个体在选择过程中被选中的概率。由于轮盘赌选择算子体现了生物进化过程中“适者生存,优胜劣汰”的思想，并且保证优良基本遗传给下一代个体。故本算法采用了轮盘赌选择算子。
3.5 交叉算子
　　交叉操作的步骤为：
　　（1） 寻找两个父代染色体的相同中间节点。
　　（2） 随机选择一个相同节点作为交叉点。
　　（3）如果父代个体交叉点前后的内容相同，则取消本次交叉操作；否则继续。
　　（4） 交换两个父代个体交叉点后的部分，产生两个子个体。
　　（5） 检查产生的两个子个体是否存在环路，如果存在则消除环路中的最大环。
3.6 变异算子
　　为了增强种群的多样性，本文提出一种新的变异操作方法来解决电力线路中的最佳抢修路径问题。
　　（1） 从变异个体X(a₀(S),a₁,…,a_i ,…,a_n(T))中随机选择一个中间节点a_i作为变异基因。
　　（2） 把与a_i相连的节点存入集合N(集合N已经提前存入计算机)。
　　（3） 在集合N中随机选择一个节点Y，当然节点Y没有出现在个体X中。
　　（4） 若Y分别和a_i-1、a_i+1相连接，则用Y替代a_i产生一条新的路径；否则取消这次变异操作。
　　（5） 重复步骤（3）到（4）直到找到一个合适的节点Y取代a_i或者搜索完集合N中的元素。
3.7 局部搜索
　　分析遗传算法的当前迭代次数Tc，若满足禁忌搜索算法的调用时机，则对遗传算法产生的新一代种群中的每个个体K调用禁忌搜索算法进行局部搜索，来弥补遗传算法较差的局部寻优性。局部搜索算法的步骤为：
　　（1） 设定参数：禁忌表长度为L，迭代次数为T_b，当前迭代次数i=0，候选解个数为m，禁忌表为空，全局最优解S_gbest=K，当前解S_local=K。
　　（2） i>T_b或者n　　（3）利用上文提到的Neighborhood(X)产生当前解的邻域解，计算邻域解的个数n。
　　（4）若n　　（5）判断m个候选解是否满足藐视准则？若成立，假设满足藐视准则的最佳候选解为Y，则S_local=Y且S_qbest=Y，修改禁忌表中各元素的任期，并将Y加入禁忌表，转步骤（7），否则，继续以下步骤。
　　（6）若存在非禁忌状态的候选解，则假设非禁忌候选解中的最佳解为Y，那么S_local=Z。同时修改禁忌表中各元素的任期，然后把Z放入禁忌表；若候选解均被禁忌，则解禁最佳候选解X，修改S_local=X。同时修改禁忌表中各元素的任期，然后把X放入禁忌表。
　　（7） i=i+1转步骤（3）。
3.8 终止准则
　　本算法采用精英保留策略，即若新一代中目标函数的最小值大于上一代目标函数的最小值，则用上一代中的最好个体替换下一代中的最差个体。如果最优个体连续10代保持不变或者达到了遗传算法的最大迭代次数T_g，则终止进化过程。
4 仿真实验和结果分析
　　仿真实验1　在MapInfo平台和VC++环境下，进行仿真实验。设置算法参数：种群规模M=10，遗传算法的最大迭代次数为T_g=50，交叉概率P_c=0.5，变异概率P_m=0.05，禁忌表长度L=3，候选解个数m=3，个体基因变异概率P_L=0.8，禁忌搜索算法的最大迭代次数T_b=5，A^*启发函数中的V_max=40km/h,起始节点S为N0.1，目标节点T为NO.39。
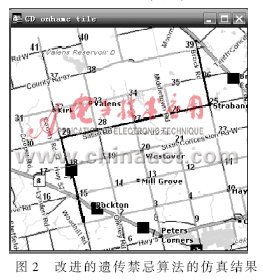
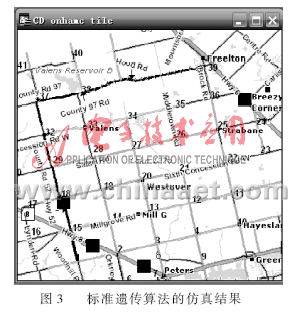
　　分别用标准遗传算法和改进的遗传禁忌算法求解此问题，仿真结果如图2和图3粗线部分所示。遗传算法得到的最佳抢修路径为1-15-18-29-32-37-38-39，适应值为35.33min。改进的遗传禁忌算法得到的最佳抢修路径为1-15-18-29-28-27-26-25-36-39，适应值为33.81min。可以看出，改进的遗传禁忌算法的性能优于标准遗传算法。

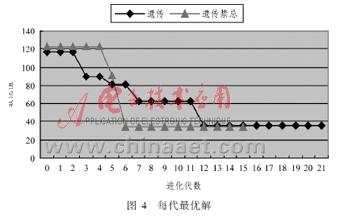
　　在实验过程中，分别记录每一代的最优个体。分析图4可以得到，遗传算法在第13代找到最优路径35.33，遗传禁忌算法在第7代找到最优路径33.81。可见，改进的遗传禁忌算法的收敛性明显优于标准遗传算法。

　　仿真实验2　在交通网络图中，抽取5个不同顶点数V，不同边数E的拓扑图G(V, E)。利用改进的遗传禁忌算法分别对这5个拓扑图求取最佳抢修路径。
　　分析表1，随着网络规模的扩大，算法的执行时间为4.2s～15.2s，得到最优解的概率为86 %～96 %。可以看出，改进的遗传禁忌算法的执行时间短，并且得到最优解的概率相对不错。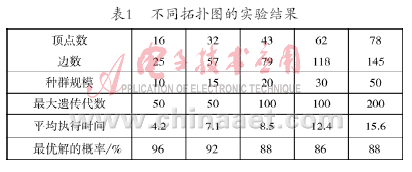

　　仿真实验3  分别利用Dijkstra、A^*算法、标准遗传算法和改进的遗传禁忌算法求取仿真实验2中给出的5个网络拓扑图的最佳抢修路径，记录其平均执行时间和得到最优路径的概率。
　　观察表2和表3的实验数据，总结有如下两条：首先，改进的遗传禁忌搜索算法的执行时间虽然比A^*算法和标准遗传算法长，但是比Dijkstra算法短。 再者，遗传禁忌搜索算法得到最优解的概率虽然没有Dijkstra高，但是高于标准遗传算法和A*算法。可见，权衡执行时间和得到最优解的概率，本文提出的遗传禁忌搜索算法相对来说是一个理想的求解电力线路最佳抢修路径的算法。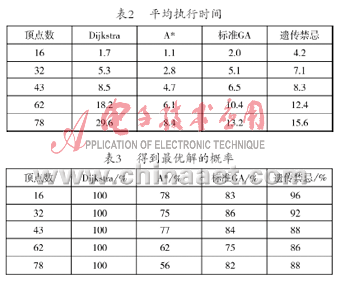

　　在分析和研究电力线路最佳抢修路径的基础上，提出了一种改进的遗传禁忌搜索算法来求解电力线路最佳抢修路径。此算法基于变异思想和A*算法来产生禁忌搜索算法的邻域解，并利用遗传算法的阶段进化思想降低调用禁忌搜索算法的频率，进而提高禁忌搜索算法的执行效率。仿真实验表明，遗传禁忌搜索算法的收敛速度和最优路径都优于标准遗传算法，并且在不同的网络规模下分析遗传禁忌算法、Dijkstra、A^*算法、标准遗传算法和遗传禁忌搜索算法表现出的优良特性。由此可见，遗传禁忌搜索算法适合于求解电力线路最佳抢修路径。

参考文献
[1]  YE Xian Yi ，CHENG Xiao Rong . Research of the best repair path based on an improved ant colony algorithm in power distribution network[C]. Transmission and Distribution Conference & Exhibition，2005：1-5.
[2]  李敏强，寇纪松，林丹. 遗传算法的基本理论与应用[M]. 北京：科学出版社，2002：120-158.
[3] 王凌.智能优化算法及其应用[M]. 北京：清华大学出版社，2001:36-37.
[4] FU Meng Yin，XUE Bin. A path planning algorithm based on dynamic networks and restricted searchiing area[C]. Proceeding of the IEEE international Conference on Automation and Logistics，2007，8：1193-1196.
[5] LI Qing ，XIE Si Jiang . Path planning algorithm for vehicles based on time-dependant optimization criterion[C]. International Conference on Control and Automation，2007，5：2360-2364.