摘要:介绍了采用三次样条曲线插值方法对称重仪表的非线性误差进行修正的方法,该修正方法对于线性误差较大的传感器有很好的补偿效果,在某些测量精度较高的场合采用三次样条曲线插值可以获得比流行的多段折线线性补偿方法更高的精度。通过对一款5位半仪表采用三种误差处理方法比较,验证了三次样条曲线插值误差补偿方法对传感器误差的补偿效果。该方法对于其他的数据采集系统精度提升有一定的借鉴意义。
一般而言,称重仪表首先接受力敏传感器的输出信号,然后对该输出信号作放大、滤波等处理后进行AD转换,然后AD转换值送CPU(MCU)处理,仪表根据CPU处理结果执行相应的功能。对于力敏传感器,包括绝大多数类型的传感器在使用过程中一般作为线性传感器来使用,而传感器从输入输出关系来说实际上都是非线性的,而将非线性的传感器作为线性来处理自然带来一定的非线性误差,而对于一款仪表而言,当设计的硬件电路较为合理时,仪表的系统误差主要取决于传感器的误差。这种将非线性的传感器按照线性处理的方法带来的结果便是:在数据采集系统中采集到的数据和实际的被测量之间存在着不一致的现象,不一致现象越严重则数据采集系统的误差就越大,这对于数据采集系统尤其是高精度的数据采集系统是要竭力避免的。
1 传感器输入输出模型
通常情况下,传感器在使用时将输入输出关系近似认为是线性关系,这样做的优点为:
1)可大大简化传感器的理论分析和设计计算;
2)为标定和数据处理带来很大方便,只要知道传感器的输入输出特性曲线上的两点(如零点和满程)就可以确定其他点的输入输出对应关系;
3)避免了非线性补偿环节,减少了数据采集系统的软硬件复杂度。
但是,传感器输入输出的实际模型为:
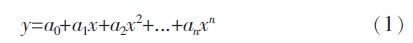
式中:a0——传感器的零点输出;a1——传感器的线性灵敏度;a2…an——传感器的非线性系数;y——传感器的输出。
由式(1)可知,由于传感器的输入输出关系遵循非线性关系,当不论采用何种线性拟合的方式,从原理上来说任何拟合直线都不能真实地反映传感器的实际输入输出关系,在某些场合下,尤其是高精度的数据采集系统,采用的传感器线性度不高时,采用直线拟合带来的误差难以忽略。当数据采集精度要求高时,寻求尽可能反映传感器的输入输出关系曲线即对传感器进行误差补偿就非常重要。根据传感器在实际标定时采用的方法(将满量程等分为若干点进行标定),采用样条曲线插值是一种较为行之有效的方法。
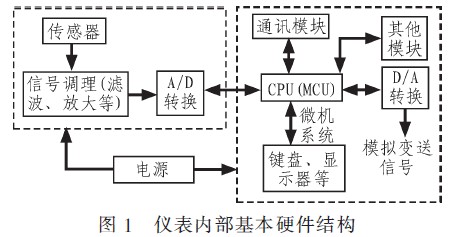
2 称重仪表的基本系统结构
仪表的硬件系统结构基本上如图1所示。首先由信号调理模块对传感器的输出信号进行放大、滤波等处理后送AD转换器进行AD转换,CPU对AD转换的结果进行相应的处理后根据处理的结果来控制相应的模块。通常情况下,在对传感器的信号进行处理时,如前文所述,传感器的输入输出关系基本上按照线性来处理,而传感器的输入输出关系实际上是非线性关系,如何尽可能降低非线性因素对系统精度的影响,对于高精度的数据采集系统而言,简单的线性处理是不够的。一般的称重仪表内部的硬件结构示意图如图1所示。
3 样条曲线插位方法
3.1 三次样条插值函数
当插值节点很多时,使用高次多项式插值并不能得到好的结果,因而一般采用分段插值法,即将插值区间分成若干个小区间,然后在每个小区间上使用次数较低的多项式进行插值。一般的分段插值法有一个严重的缺点,就是会导致插值函数在子区间的端点处不光滑,而样条曲线插值就不存在这个问题。三次样条插值由分段三次曲线连接而成,在连接点处有二阶连续导数,从而可以保证在连接点处光滑连接。
设函数f(x)在区间[a,b]上给定n+1个插值节点:a=x0
1)S(x)在每个小区间[xj,xj+1]上是三次多项式j=0,1…,n-1;
2)S(x)在每个小区间[a,b]上具有连续二阶导数;
3)S(xj)=f(xj),j=0,1…n(2)则S(x)为函数f(x)的三次样条插值函数。
3.2 三次样条插值函数求法
记S"(xj)=Mj,S(xj)=yi,hj=xj+1-xj,由三次样条插值函数定义知,三次样条函数的二阶导数S"(xj)在每个小区间[xj,xj+1]是一次线性函数,如果已知在小区间两个端点的值,则S"(x)的在小区间[xj,xj+1]表达式可表示为:
<img src="http://files.chinaaet.com/images/2012/02/24/6bb64ee5-1c2b-4e70-a09b-40fff882a1cf.jpg" _cke_saved_src="http://files.chinaaet.com/images/2012/02/24/6bb64ee5-1c2b-4e70-a09b-40fff882a1cf.jpg" alt="S" (x)的在小区间[xj,xj+1]表达式"=""></p><p> </p><p>其中的f[xj,xj+1]是关于节点xj,xj+1的一阶差商。对于各个区间内的三次样条插值函数可以通过采用追赶法对三弯矩方程组求得样条函数的系数Mj,然后将系数Mj代入公式(4)求得,具体介绍可参看参考文献。</p><p></p><p>4 称重仪表的三次样条插值误差补偿</p><p></p><p>4.1 基于三次样条插值的误差补偿方法</p><p></p><p>对仪表进行三次样条插值误差补偿的方法和步骤为:</p><p></p><p>1)首先将传感器的满量程划分为若干段(一般为等间距划分),确定插值节点;</p><p></p><p>2)给传感器在各个插值节点处施加标准载荷,记录此时的ADC转换值和实际显示值,根据理想的显示值和实际显示值求得一偏移量和ADC转换值求代数和,将此值作为该插值节点的输入值xj;</p><p></p><p>3)将各个插值节点处的仪表应该显示的值(理想显示值)作为输出值yj;</p><p></p><p>4)根据各节点处的xj和yj求得各个区间上的三次样条插值函数Sj(x);判断ADC的实时转换值x所处的具体区间,按照该区间的三次样条插值函数计算仪表的实际显示值即实时载荷值;</p><p></p><p>4. 2 实验数据处理和分析</p><p></p><p>采用一款已经研制完成的五位半精度的仪表对传感器的信号进行分析和验证。</p><p></p><p>本款仪表采用高精度的24位AD转换器AD7190对传感器信号进行数模转换,MCU采用TI公司的MSP430F149。</p><p></p><p>AD7190是ADI公司最新推出的具有业内最高精度之一的∑—△型AD转换器,其非线性误差最低仅为0.000 5%,峰值转换速率可达到4.8 kHz,且具有极低的温漂和转换噪声等性能。当内部PGA为1时可以达到高达22.5bit的无噪声输出,实际设计时,选取19位有效位(已经超出5位半显示精度要求)。同时AD7190内部自带有零点校准功能和增益校准功能,通过软件编程可方便地根据实际情况对内部的零点校准寄存器和增益校准寄存器进行操作。</p><p></p><p>传感器输出的差动信号首先经过高精密双运放OP2177实现倍数为64倍的差动放大,AD7190的内部PGA设为2,这样可以实现对传感器输出信号实现具有极低噪声的128倍放大,选取19位有效位时可以实现不跳码的AD转换字输出,而这是实现高精度误差补偿非常关键的要素。仪表内部具有软件集成的三次样条插值非线性补偿模块。实际使用时,只要打开该补偿模块,给传感器分别施加若干个标准重量,再通过相应的仪表操作便可以实现对传感器的非线性误差修正。</p><p></p><p>MSP430F149是TI公司生产的高性能的基于RISC体系结构的混合信号16位单片机,具有较强的数据处理运算能力,32 kB的FLASH和2 kB的SRAM保证了足够的代码空间和数据存储空间。</p><p></p><p>仪表内部信号调理模块结构示意图如图2。</p><p></p><p></p><p><img src="http://files.chinaaet.com/images/2012/02/24/21842371-7f56-4eca-9639-895228b558fe.jpg" _cke_saved_src="http://files.chinaaet.com/images/2012/02/24/21842371-7f56-4eca-9639-895228b558fe.jpg" alt="仪表内部信号调理模块结构示意图"></p><p></p><p> <br> </p><p></p><p>称重仪表三次样条插值非线性补偿的具体的工作原理和工作过程见前文所述。</p><p></p><p>为方便和简化数据处理和分析过程,选取一量程为9公斤的力敏传感器,在给传感器施加载荷前先进行仪表的零点校准和系统校准(即对AD7190进行偏移和增益校准),使得空载时为0,满程时为90 000。依次对传感器施加1公斤的标准砝码(即将传感器的满量程等分为9个区间),将实时的ADC转换器的转换值直接读出,得到的一组数据如表1。</p><p></p><p></p><p><img src="http://files.chinaaet.com/images/2012/02/24/0f84f519-8d83-45e5-a5e7-0d7094fe40f8.jpg" _cke_saved_src="http://files.chinaaet.com/images/2012/02/24/0f84f519-8d83-45e5-a5e7-0d7094fe40f8.jpg" alt="ADC转换器的转换值"></p><p></p><p>对表1的数据分别采用不补偿、分段线性补偿(通常的仪表内部的折线功能)、三次样条插值补偿方法进行处理,然后对传感器施加载荷,由于对仪表采用三次样条插值和分段线性插值补偿后,在插值节点处的误差为零,所以选取载荷为各个分段区间的中间值,得到的数据如表2所示。</p><p></p><p></p><p><img src="http://files.chinaaet.com/images/2012/02/24/d2924475-b512-4d7f-9935-781120fee2a3.jpg" _cke_saved_src="http://files.chinaaet.com/images/2012/02/24/d2924475-b512-4d7f-9935-781120fee2a3.jpg" alt="各个分段区间的中间值"></p><p></p><p>其中的分段线性补偿是目前仪表较为流行的一种误差补偿方法,其思想和三次样条插值误差补偿的思想基本一样,两者的差别是分段线性补偿在各个分段区间内进行线性计算,而三次样条插值误差补偿在各个分段区间内进行非线性计算。分段线性补偿处理方法相对简单,对传感器的非线性误差有一定的补偿作用,但对于高精度的数据采集系统该方法有时难以达到精度要求。</p><p></p><p>三种处理方法误差曲线分布如图3所示。</p><p></p><p></p><p><img src="http://files.chinaaet.com/images/2012/02/24/3fa42332-e06e-4d22-929b-c07548f9775d.jpg" _cke_saved_src="http://files.chinaaet.com/images/2012/02/24/3fa42332-e06e-4d22-929b-c07548f9775d.jpg" alt="三种处理方法误差曲线分布"></p><p></p><p>由表2和图3可得:</p><p></p><p>1)未补偿时,该仪表的满量程非线性误差为:119/90000=0.13%FS;其绝对误差在2 Kg处达到最大值119,在1 Kg处的相对误差达刭最大值0.8%;</p><p></p><p>2)采用分段线性补偿时,该仪表的满量程非线性误差为:40/90000=0.044%FS;其绝对误差在2.5 Kg处达到最大值40,0.5 Kg处的相对误差达到最大值0.18%;</p><p></p><p>3)采用三次样条插值补偿时,该仪表的满量程非线性误差为:13/90000=0.014%;其中绝对误差在7.5 Kg处达到最大值13,在0.5 Kg处达到相对误差最大值0.08%;</p><p></p><p>5 结论</p><p></p><p>通过三次祥条插值函数对仪表进行补偿可以得到较高的精度,满量程非线性误差、满量程内最大相对误差和最大误差都得到很好的改善,即使是传感器在低端呈现凹形特征和高端呈现凸形特征较为严重的情况下依然可以得到较高的精度,相比于分段线性补偿,其补偿的精度也大为提高。当插值点较少时,三次样条插值误差补偿的精度要比分段线性插值的误差要小得多。采用三次样条插值函效对仪表或其他的数据采集系统的误差进行补偿,除了可似很大程度上减少传感器非线性对精度的影响,还可以降低信号调理电路和AD转换器对系统精度的影响。</p><p></p><p>同时应注意到,对于有较高精度要求的数据采集系统,为获得较好的三次样条插值误差补偿效果,高精度的信号调理电路、AD转换器的稳定性是至关重要的。</p><p></p><p>另外适当选取插值节点数也非常关键,节点数选择过少,达不到较好的补偿效果,节点数过多不但造成计算量加大,还有可能造成在某些分段区间误差过大,从而达不到很好的补偿效果。一般的插值节点数选择在10~25个左右为宜。</p><p> <br> </p><p></p>

