摘  要： 针对一维下料优化问题，根据企业的实际生产情况，考虑能够满足和不满足生产两种情况，建立一个新的优化模型，并使用蜂群遗传算法求解方案。用各零件长度的一个排列作为一个染色体，每个零件的长度作为染色体的一个基因，根据蜂群原理设置两个不同的种群，种群1用于全局搜索，种群2用于局部搜索。实验结果表明，该模型具有一定的实用价值。
关键词： 一维下料问题；优化下料；蜂群遗传算法；染色体；种群；抑制算子

    下料问题是将库存的原材料切割成形状不同、大小不一或是长短各异的多种零件以满足顾客的需求，在钢铁企业、造纸业、纺织业和木材加工业中都有着广泛的应用，Dyckhoff[1]和Wascher[2]就下料问题给予了全面的分类。根据原材料和零件维数的数目，可以把下料问题划分为一维下料问题、二维下料问题和多维下料问题。
    一维下料问题是其中一个重要的组成部分，讨论该问题是研究二维、三维等多维下料问题的基础。不同学者在对待这个问题时也有着不同的研究重点，例如考虑最大限度地节约原材料，提高原材料利用率；如何减少排样方案数；或是优先使用较短原材料、增加最后一根余料长度；在规定的交货期前完成生产任务等不同目标。经过调查发现，大部分研究一维下料问题的文献很少考虑企业面临生产力不足的情况，这时企业会面临一定的损失或者盈利下降的问题，参考文献[3]考虑了有交货期限制的一维下料问题，通过合理安排生产进度来减少延迟所造成的损失；而参考文献[4]、参考文献[5]虽然针对不完全下料这种情况提出了解决方案，但也仅仅在如何提高原材料的利用率上加以研究，其他与此相关的文章也鲜见发表。任何时候企业的生产能力都是有限制的,包括加工能力和原材料储备，而生产出来的各种零件也因为其市场价值或后期加工需求的紧迫程度不同所带来的收益也不尽相同，当企业不得不面对这些突发情况时，合理安排价值高、需求紧迫的零件优先生产、同时尽可能多地减少废料、使企业的损失最小成为决策者必须考虑的问题之一，本文在这种情况下针对单一规格原材料的一维下料问题给出了一个以价值导向为基础的、将问题实际量化的新模型。
1 模型结构
    模型的建立需要考虑将两个问题同时融入其中：一是企业自身能力可以满足生产需求，包括生产能力满足和原材料库存充足，在这种情况下，下料方案所产生的废料最小，原材料的利用率最高是决策者所关心的主要方面，这时模型所要解决的就只是充分利用原材料的问题；另一个方面是因为客观原因导致的生产力受限或因为上游企业原材料供应不上而导致无法按时完成全部的生产任务，此时，将需求紧迫和延迟交货所造成的损失价值高的零件优先安排生产，保证企业总的损失最小是主要目标。
    具体参数设定如下：假设企业共需要生产m种零件，i为待生产零件的编号，li为第i种零件的长度，vi为第i种零件对应的市场价值，di为第i种零件的需求数量，L则为原材料的长度，v为其单位价值，n为生产中使用的原材料总数量，aij为j号原材料所生产的第i种零件的数量，cj为j号原材料切割完毕后剩下的余料的长度，E为企业的生产能力或是原料总量限制。具体模型如下：
  
    目标函数（1）保证了企业的总体损失最小，当满足生产时，目标变为使生产结束后产生的废料损失最小；式（2）确保企业的生产总量不会超出需求的数量，使得产需平衡，这里认为超额生产的零件会带来库存、管理、耗损等一系列费用，同样视为损失；式（3）则确保在一根原材料上生产出的零件长度之和不会超过原材料自身的长度，否则生产是无法进行的；式（4）限制企业实际能够生产的零件数量。
2 蜂群遗传算法
    根据上述已经建立的模型，采用应用较多的遗传算法求解问题。遗传算法最早是在20世纪60年代末～70年代初由美国密歇根大学的Holland教授及其学生提出的。本文采用一种基于蜂群繁殖原理的改进型遗传算法[6，7]，这种算法既能保证最优个体的存活和交配的权利，又能保持种群中个体的多样性。
    在自然界中，整个蜂群是由蜂后、雄蜂和雌蜂三部分组成的，每个蜂群中有且仅有一只蜂后，蜂后也是整个蜂群中唯一一个具有生殖能力的蜜蜂。蜂后如果死亡或者失去繁殖能力，若干潜在可能成为新蜂后的雌蜂会互相竞争，直到一只胜出成为新一代的蜂后。蜂后会产生两种类型的后代，一种发育成雌蜂，数量较多，没有生育能力；而另一种则发育成雄蜂，数量较少，只负责和蜂后进行交配。
    根据蜂群的生育原理，文中的蜂群遗传算法的种群是由蜂后、雄蜂群和雌蜂群三者组成，其中蜂后的数量为1，雄蜂群个体的数量为N，雌蜂群个体的数量为M。
2.1 适应度函数
    文中所述一维下料问题的优化目标是使得下料方案的总损失最小，用适应度函数来评价算法时，一般规定适应度越大解的质量越好。根据上述原因，本文将适应度函数取为：
  
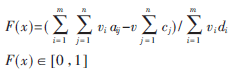
其中，分子是已生产零件的价值总和减去废料的价值之和，分母为总需求零件的价值和，只有当需求满足且没有余料时，适应度函数值可以达到最大，取值为1，即原材料利用率达到了100%。
2.2 染色体编码
    编码方式也称为基因表达方式，种群中的每个个体即每个染色体由基因构成。本文中染色体的编码采用零件全排列组合方式，即个体中的每个基因代表一个零件，例如由要切的1个3号零件、2个2号零件、1个8号零件、3个5号零件随机产生的编号序列(2，5，3，8，2，5，5)就是一个个体。译码时，取一根原料，按顺序从编号序列中取一个零件配切，直到所取的零件不能在此原料上配切为止，然后从序列中删去已配切的零件编号，再取一根原料，对剩下的零件编号序列重复以上步骤直到生产满足或是原材料用尽。
2.3 遗传算子的选择
2.3.1 交叉算子
    雄蜂群按照交叉率和蜂后进行交叉操作，有利于产生新的高适应度的个体。交叉后产生一雄一雌的后代。用雄性后代取代父代，雌性后代临时存放，以便作下一步处理。雄蜂群主要是为了保持较高的选择压力，以提高收敛速度。交叉是最重要的遗传算子，本文中交叉算子的设计采用顺序交叉方案，首先随机确定两个交叉位置，在交换交叉点之间的片段后，从第2个交叉位置起在原先父代个体中，删除从另一个父代个体中交换过来的基因，然后从第2个交叉位置后填入剩余基因，从而生成两个新的染色体。
2.3.2 变异算子
    变异可以提供初始种群中所没有的染色体，为种群提供新的内容。变异算子的设计多采用多点交换变异的方案，本文采用的变异算子皆为两点变异，即在每个染色体中以概率P随机选取染色体上的两点进行交换。变异概率控制着新基因导入种群的比例，若太低，一些有用的基因就难以进入选择；若太高，则会造成后代失去双亲继承下来的好特性。
2.3.3 选择算子
    雌性蜂群按照锦标赛选择的方法，将交叉后产生的雌性后代和原雌性蜂群中的个体进行选择，重新组成M个个体的新雌蜂群。选择方法为：两个群体各随机抽取x个个体进行比较，适应度高者保留，直到满足新群体规模。这个新的雌性蜂群和原来的雌蜂群在个体上存在了一定数量的差异，所以需要重新选择蜂后，方法是从新群体中选出适应度最大的个体与蜂后比较，若适应度高于原蜂后，那么就取代原蜂后；否则，原蜂后不做改变。锦标赛规模一般取为2。
2.3.4 抑制算子
    蜂后为了维持自身的地位，需要对编码相似程度较高的染色体进行抑制，抑制的阈值为T。具体的抑制方法是：若雌蜂群中的某些个体与蜂后之间的欧式距离D≤T，则进行抑制，删除这些个体并以随机个体取代。其他没有被抑制的个体按照变异率进行变异。雌蜂群的目的主要是为了保持种群的多样性，避免种群早熟收敛，随时可以跳出局部峰值。欧式距离D表示如下：
    
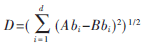
其中参数d为染色体的长度，Abi为A染色体的第i个基因位，Bbi为B染色体的第i个基因位。
2.3.5 算法描述
    蜂群遗传算法BSGA(Bee-Swarm Genetic Algorithm)的过程描述为：
    (1)随机产生两个群体，雄蜂群和雌蜂群，每个种群各有N和M个个体，在雌蜂群中选出适应度最大的个体做为蜂后；
    (2)雄性个体经过轮盘选择操作，按固定的交叉率与蜂后进行交叉，产生一个雄性和一个雌性后代，然后再进行变异操作；
    (3)雌性蜂群按照锦标赛选择的方法，将新产生的雌性后代和原雌性蜂群进行选择操作，重组为新的M个个体的雌蜂群；
    (4)对新产生的雌性群体实行蜂后排挤机制，对群体中与蜂后的欧式距离D在一定阈值之内的个体予以消灭，再随机生成新的雌性个体，补齐该种群所消灭的个体的数量；
    (5)若算法条件不满足，回到过程(3)；否则，输出蜂后作为全局最优解；
    (6)算法结束。
3 仿真案例分析
    仿真程序采用PB编程，设置雄性种群数目为50，雌性种群数目为50，染色体的交叉概率为0.8，变异概率为0.005，迭代最大次数为100次。
    算例1：计算参考文献[7]中的例子。现需总长度2 104 m，长度分别为4 m、6 m、10 m、13 m、14 m、19 m、20 m、21 m、22 m、28 m、32 m、33 m、36 m、38 m、38 m、40 m、41 m、42 m、48 m、48 m、50 m、55 m、57 m、60 m、64 m、66 m、67 m、72 m、76 m、77 m、83 m、84 m、85 m、86 m、91 m、91 m、94 m、94 m、99 m、100 m的网线40段，求所需每箱长度为305 m的网线箱数及分割方案。因为本文中的目标函数和适应度函数中有价值系数的存在，所以赋予零件和原料每米相同的单位价值1，具体价值和长度不同的例子将在算例2中讨论。
    表1给出了利用本文给出的算法计算得到的结果，网线需要7箱，合计余料31 m，其中除了最长的那箱余料31 m，材料利用率为89.84％，其余的都加以充分利用。

    模型主要考虑解决的问题是不能完成全部生产任务时的情况，如何尽可能地在有限的资源内创造较高的价值是本文所关心的问题，在此给出算例2：假设需求10种零件，长度分别为135 cm、31 cm、23 cm、92 cm、28 cm、257 cm、14 cm、110 cm、55 cm、147 cm，需求量分别为75、250、250、45、200、50、920、67、100、15个，零件价值分别为217、44、30、113、33、450、18、169、63、277元，原料长度为600 cm，单位价值为0.5元。仿真结果如表2所示。

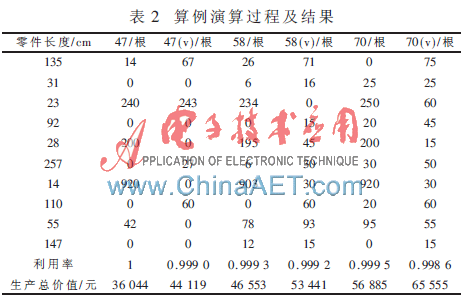
    从仿真结果中可以看到，在原材料不足（这里仅考虑原料不足的状况，生产力不足的情况和此类似）时，需要考虑的是尽可能多地生产产品，创造价值。(v)表示考
虑价值因素影响的切割方式，通过仿真结果中的数据对比可以看到，原料不满足生产时，如果以价值为导向进行切割，将比不考虑价值因素的切割方式得到更多的利润，这样可以保证在突发情况下尽可能多地创造出价值。这时，企业可以把带来价值高的自己进行生产，而将其余产品的加工进行外包等其他形式进行。实验数据也证明了本文中提出的模型具有一定的实际使用意义。
    本文针对企业实际的一维下料问题，运用蜂群遗传算法求解。从实例结果来看，在保证最高生产价值的同时，原材料的利用率也令人满意，对于在实际生产中应对突发状况是很有意义的。
参考文献
[1] DYCKHOFF H.A typology of cutting and packing problems [J].European Journal of Operational Research，1990，44(2)：145-159.
[2] WASCHER G，HAUSSNER H，SCHUMANN H.An improved  typology of cutting and packing problems[J].European Journal of Operational Research，2007，183(3)：1109-1130.
[3] HARALD R，VOSSEN W M.The one-dimensional cutting stock problem with due dates[J].European Journal of Oper ational Research，2010，201(3)：701-711.
[4] 李培勇.多规格一维型材优化下料[J].机械科学与技术，2003，22(Z1)：80-83.
[5] POLDI K C，ARENALES M N.Heuristics for the one-dimensional cutting stock problem with limited multiple stock  lengths[J].Computers and Operations Research，2009，36(6)：2074-2081.
[6] 吴迪，崔荣一.蜂群遗传算法[C].中国人工智能学会第11届全国学术年会论文集，2005：733-736.
[7] 吴迪，李长荣，宋广军.基于蜂群遗传算法的一维优化下料问题[J].计算机技术与发展，2010，20(10)：82-85.