摘 要：针对目前多传感器数据融合过程中传感器对某一状态量测量时精度较低的问题，提出了基于最小二乘原理的多传感器加权数据融合算法。该方法利用最小二乘原理和方差的遗忘信息,通过均方误差比较，计算出各个传感器的权重之后进行加权融合。该算法既考虑了历时信息的作用,又考虑了环境噪声和新采样值的影响，增强了对环境监测的敏感性。相比同类融合方法，该方法具有较高的精度，最后仿真结果也直观地说明了该方法的有效性。
关键词：数据融合；多传感器；均方误差；最小二乘

     在自动化系统或科学实验中，需要用多个传感器在不同的方位对同一目标参数进行测量，但由于传感器所处的方位不同和传感器自身质量的差异，以及受一些无法控制的随机因素的作用，在实际中各个传感器所测量的参数值必存在偏差，这样就存在如何确定对测量数据进行融合的问题[1]。多传感器数据融合就是将来自多个传感器的数据或信息进行综合处理，所获得的结果比单一传感器测量值更为准确，能够更灵敏地检测动态系统的变化。
    在多传感器加权融合估计中，关键是如何为各传感器分配合适的权重。加权平均法不考虑各测量数据的准确性，取同样的权值直接求平均值，该算法计算简单，实现较为容易，但是误差较大。参考文献[2]提出一种相关估计器，融合了最小均方估计(LMS)和小波降噪的方法，对多个输入进行算术平均，所得的平均值使用小波降噪滤波器进行降噪。由于LMS估计中采用的是算术平均法，因此不是最优估计[2]。参考文献[3]主要针对恒窗长方差运算对噪声变化跟踪能力不强的缺点提出了自适应窗长方差估计在多传感器数据融合中的应用。该算法能灵敏地跟踪传感器测量噪声的突变，同时不依赖于初始窗长的设定，能自动收敛到合适的窗长，该算法主要用于非平稳信号多传感器数据融合[3]。参考文献[4-6]采用基于最小二乘原理融合算法，推导出各个传感器的权系数与测量方差的关系，从而对各传感器的权值进行合理的分配。参考文献[7]提出了迭代计算各节点测量数据的无偏估计值，以归一化后的各传感器测量值与无偏估计的欧氏距离作为权值进行加权平均。参考文献[8]提出了一种分批估计法,通过将各传感器均分成两批，在计算每批的样本均值和样本方差后采用方差加权进行融合处理。参考文献[9-11]提出了小波去噪法，通过去除测量中的噪声，进行数据融合。参考文献[12-14]提出了卡尔曼滤波法，利用卡尔曼滤波器及其估计误差协方差阵分别与传感器及其测量方差相对应，对多组卡尔曼滤波加权融合。本文采用了基于最小二乘原理多传感器加权数据融合算法，综合考虑传感器的内部噪声与环境干扰等多种因素,充分利用测量数据中的冗余信息，使冗余系统测量数据的估计进一步提高。


1.3 遗忘因子σ选取
    遗忘因子的作用是加强新的数据提供的信息量，逐渐削弱旧的数据，以突出新的数据。它能综合考虑传感器的内部噪声与环境干扰等多种因素，实时方差的利用增强了对环境干扰的敏感性，历次方差则更好地体现了传感器自身因素对测量值的影响。根据公式:
    
2 算法验证与仿真
    本文用Matlab软件对上述理论推导结果作仿真验证。设待测信号的真值为y(t)=1+sint,被6个传感器所测量。假设6个传感器相互之间互不影响，它们分别单独地加入均值为0、方差为0.01、0.03、0.05、0.10、0.15的高斯白噪声,并分别均匀地采集了300个点。图1为4种方法在一次试验中均方误差各个时刻曲线比较图。

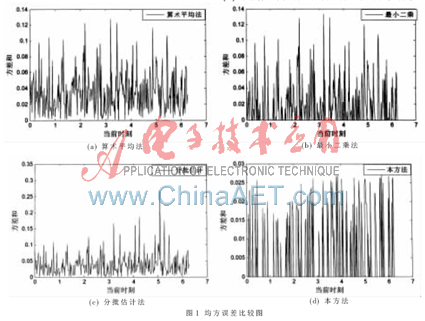
    从图1中可以看出，各个时刻均方误差由大到小依次为算术平均法、最小二乘、分批估计与本方法。利用基于最小二乘和遗忘因子方法均方误差与各个时刻比较平均。把各个时刻的均方误差相加，算术平均法、最小二乘、分批估计和本方法随机试验100次得到图形如图2所示。从图2中可以看出本方法均方误差和最小。

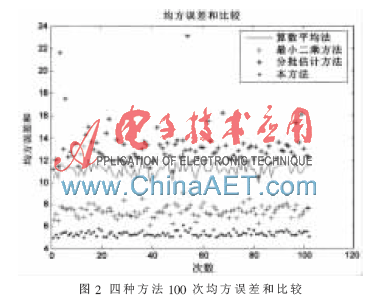
    多传感器在对某一参数进行测量时，因受传感器自身因素和环境的影响，会有不同的测量结果。多传感器数据融合可以有效地利用重复冗余的信息，提高量测信息的估计精度。本文提出了基于最小二乘和遗忘因子的多传感器数据融合算法，对实验数据进行了融合处理，可以看出与其他3种方法相比估计精度显著提高。本方法可以用于获取被测参数量估计值的动态系统中，因此该算法具有较强的实用性。
参考文献
[1] 刘建书,李人厚,常宏.基于相关性函数和最小二乘的多传感器数据融合[J].控制与决策,2006,21(6):714-716.
[2] MAJUMDER S,SCHEDINGAND S,DURRANT-WYHTE H F.Multi-sensor data fusion for underwater navigation[J].Robotics and Autonomous System,2001(35):97-108.
[3] 张怡,贾民平.自适应窗长方差估计在多传感器数据融合中的应用[J].传感技术学报,2008,21(8)：1398-1401.
[4] 仲崇权,张立勇,杨素英,等.基于最小二乘原理的多传感器加权融合算法[J].仪器仪表学报,2003,24(4):427-429.
[5] Song Kaichen, Nie Xili. Adaptive fusion atgorithms based on weighed least square method[J]. Chinese Journal of Mechanical Engineering,2006,19(3)：451-454.
[6] 李雪莲,孙尧,莫宏伟.基于最小二乘的冗余信息数据融合算法实现[J].计算机工程与应用,2009,45(15)：34-39.
[7] 马琦，张记龙，王志斌.无线传感器网络簇内自适应融合算法研究[J].计算机应用研究,2009，26(7)：2502-2503.
[8] 张西良,孙优.无线传感器网络基于定向扩散与分批估计的数据融合算法[J].传感器与仪器仪表，2006,22(9)：173-176.
[9] 李超,胡谋法，刘朝军，等.基于小波的多传感器空间目标数据融合算法[J].信号处理,2006,22(4):203-207.
[10] Xu Lijun, Zhang Jianqiu,Yan Yong. A wavelet-based mutilsensor data fusion algorithm[J]. IEEE Transactions on  Instrumentation and Measurement, 2004,53(6):1539-1545.
[11] 高羽，张建秋.小波变换域估计观测噪声方差的Kalman滤波算法及其在数据融合中的应用[J].电子学报,2007,35(1):108-111.
[12] SUN S L, DENG Z L. Multi-sensor optimal information  fusion kalman filter[J]. A Utomatica,2004,40(6):1017-1023.
[13] SUN S Ｌ． Multi-sensor information fusion while noise filter weighted by scalars based on Kalman predictor[J]. Automation,2004,40(8):1447-1453.
[14] 蔡鹤皋，金明河，金峰.卡尔曼滤波与多传感器数据融合技术[J].模式识别与人工智能,2009,13(3):248-254.
[15] 施雨,李耀武.概率论与数理统计应用[M].西安：西安交通大学出版社,1998.