摘 要: 多关节机器人的工作空间是反映机器人运动能力的一个重要指标。提出了一种简化的多关节机器人工作空间仿真方法,可以不用求解正运动学方程,只要根据简单的机器人关节变换参数就可以通过仿真迅速得到其运动空间。以Brokk50机器人为例,首先建立其D-H变换坐标图并确定变换参数,然后以Matlab为仿真工具建立仿真模型并验证参数正确性,最后运用提出的新方法快速求出其运动空间。从而能够为多关节机器人的设计改进、遥操作和轨迹规划等工作提供参考。
关键词: 多关节机器人;工作空间仿真;Matlab仿真
多关节机器人是一种应用非常广泛的机器人,绝大部分工业机器人和智能移动机器人都是多关节机器人,拥有多关节机械臂。机器人在农业上可以完成蔬菜和水果的采摘,在工业上的应用更是比比皆是,如各种喷涂和焊接机器人。对机器人的应用大大降低了工人劳动强度,降低了劳动成本,提高了工作效率,具有很大的应用价值。多关节机械臂的灵活程度对其工作能力有着至关重要的作用[1-2]。关节臂的工作空间是多关节机器人灵活程度的重要指标之一,它是指其末端参考点所能达到的空间点集合。目前,机器人工作空间的仿真通常通过建立机器人的正运动学方程,然后求解机器人的末端坐标,最后将末端坐标点集合显示在坐标图中加以实现,这通常需要大量的矩阵运算,步骤繁琐工作量大,极易出错。本文在Robotics Toolbox仿真工具箱的基础上,提出了一种简化的工作空间仿真方法,只要知道机械臂模型和相关参数,不需要进行正运动学解,即可求出末端坐标,进而求出工作空间的仿真图。可供设计者、操作员和运动规划者分析工作问题,制定工作策略。
1 机器人模型建立和参数
本文以Brokk50为例,首先画出其简化的机械臂模型,然后确定关节间D-H变换参数[3-4],最后通过仿真验证参数的正确性。Brokk50机器人的机械臂简图如图1所示。
为了方便查看,图1中将坐标系0和坐标系1的原点放在了一起。
oxyz:与固定坐标相连的固定参考坐标系,称为基坐标系。
onxnynzn:与机器人的第n个杆件相固连,坐标原点在第n+1关节的中心点处。
确定和建立每个坐标系遵循以下3条规则:
(1)zn-1轴沿着第n关节的运动轴;
(2)xn轴垂直于zi轴及zi-1轴并指向离开zi-1轴的方向;
(3)yn轴按右手坐标系的要求建立。
同时,刚性杆件的D-H表示法取决于连杆的以下4个参数:
(1)连杆长度an:表示沿xn轴方向zn-1轴与zn轴之间的距离;
(2)连杆扭角αn:表示绕xn轴线由zn-1轴到zn轴所旋转的角度;
(3)连杆间距dn:表示沿zn轴方向xn-1轴到xn轴的距离;
(4)转角变量θn:表示绕轴由xn-1轴到xn轴所旋转的角度。
由图1和机械臂参数可以确定连杆参数和变量,如表1所示。


其中,转角变量θi为关节绕z轴的旋转角度,是未知量;连杆间距为相邻关节间公垂线的距离;连杆长度为已知;连杆扭角αn为相邻两个z轴的夹角。
2 Brokk50机器人建模仿真
对于机械臂的运动学、动力学以及轨迹规划分析,可以使用基于Matlab平台的机器人工具箱—Robotics Toolbox,此工具箱最新版本在2002年4月由Peter I.Corke更新。该工具箱函数可以在Matlbab7.1版本上运行。它提供给用户一些常用的函数,可以实现机械臂运动学、动力学仿真,是一款非常方便和容易上手的辅助工具[5-6]。
下面使用工具箱中的函数对Brokk机器人机械臂进行建模和正运动学仿真,具体实现函数如下:
L1=link([pi/2 0 0 40],'standard');
L2=link([0 60 0 0],'standard');
L3=link([0 80 0 0],'standard');
L4=link([0 60 0 0],'standard');
L5=link([-pi/2 50 0 0],'standard');
r=roBot({L1 L2 L3 L4 L5});
r.name='Brokk机械臂';
q=[0 0 0 0 0];
driveBot(r,q)
link函数中的参数从前到后分别代表D.H参数表中的α、a、θ、d;standard表示采用的是标准D.H建模方法;roBot函数作用是将机械臂各杆与关节连接起来;q表示关节变量的初始角度;driveBot是绘制机械臂的函数。这里取L1、L2、L3、L4、L5分别为40、60、80、60、50。采用工具箱函数得到的仿真结果如图2所示。其中x、y、z分别表示抓持器的位置;ax、ay、az表示抓持器的姿态,是用RPY旋转来表示的,ax表示偏航角,ay表示俯仰角,az表示滚动角;q1、q2、q3、q4、q5为5个关节角度值。由图2可以看出机械臂参数正确,可以进行工作空间分析。

3 机械臂工作空间仿真方法
本文采用一种不需要正运动解算的机器人末端坐标求取方法,改进了传统的空间求取方法——蒙特卡洛方法。可以快速求出机器人的末端坐标并得到工作空间图像,计算速度快,适合任何关节型机械臂工作空间求解,只需要具有大致模型和参数。具体求解步骤如下:
(1)根据机器人参数确定参数值和变化范围;
(2)利用随机函数RAND(j)(j=1,2,…,N)产生N个0~1之间的随机值,由此产生的随机步长为(qmaxi-qmini)×RAND(j),得到机械关节变量的伪随机值为[7]:
qi=qmini+(qmaxi-qmini)RAND(j)
式中qmaxi、qmini为关节变量的上下限,i为关节数目;
(3)将N个关节变量组合带入Robotics Toolbox公式 fkine(机器人名,c)中,得到机械臂末端运动矩阵,并提取x、y、z坐标分别存于矩阵X、Y、Z中;
(4)通过plot3(x,y,z)和plot(x,y)、plot(x,z)、plot(y,z)得到工作空间的点集云图。
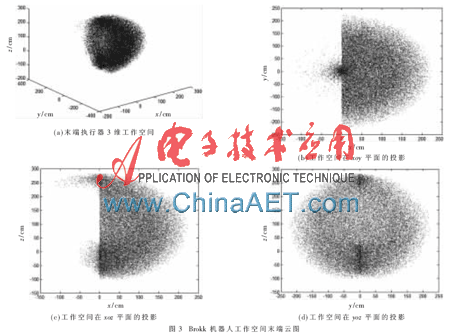
Brokk50机器人工作空间的仿真结果如图3所示。
灵活运用基于Matlab平台的机器人工具箱——Robotics Toolbox,可以在仅仅知道机械臂的部分参数的情况下快速建立机械臂仿真模型,并在不计算机械臂运动学正解的情况下得出工作空间,减少了大量复杂的矩阵运算,提高了工作效率。可以直观地指导机械臂的设计工作,确定设计参数;也可以为遥操作和轨迹规划提供一些理论支持,减少实际调试时间,优化运动轨迹,避免机构干涉等问题。
参考文献
[1] 郁邦永,茅献彪.机械手工作空间分析与仿真系统探讨[J].煤矿机械,2012,33(8):68-70.
[2] 梁喜凤,王永维,苗香雯,等.番茄收获机械手工作空间分析与仿真[J].浙江大学学报(农业与生命科学版),2005,31(6):807-811.
[3] 任崇轩.五自由度机械臂运动和控制仿真分析[D].广州:华南理工大学,2012.
[4] 马江.六自由度机械臂控制系统设计和运动学仿真[D].北京:北京工业大学,2012.
[5] 冯飞,张洛平,张波.四自由度机器人Matlab仿真实例[J].河南科技大学学报(自然科学版),2008,29(3):24-26.
[6] 康嘉瑞,樊留群,LAURISCHKAT R.基于Matlab的机器人逆运动学研究[J].佳木斯大学学报(自然科学版),2008,29(3):24-26.
[7] 田海波,马宏伟,魏娟.串联机器人机械臂工作空间与结 构参数研究[J].农业机械学报,2013,44(4):196-201.

