文献标识码： A
文章编号： 0258-7998(2014)06-0074-04
冠心病是人类主要的致死疾病之一。冠心病的手术治疗方法是体外循环冠状动脉旁路移植手术，但是手术中心脏停跳会给病人带来术后并发症[1]，不仅增加了医疗成本而且大大延长了病人术后恢复的时间。为了解决这一问题，医生希望采用非体外循环的方法，即在手术过程中采用使心脏始终保持在完全跳动状态(区别于使用机械静止器的非完全跳动的情况)的手术方式完成操作。由于心脏运动信号运动快、幅度大，医生无法手工跟踪心脏运动来完成手术[2]。如今随着机器人技术的发展，机器手臂可以帮助医生跟踪心脏运动来完成心脏不停跳的非体外循环旁路移植手术。其工作是消除机器人手术工具端点与心脏表面某操作点的相对运动，使得机器人与心脏保持相对静止。医生在此基础上，通过操作手柄叠加运动完成远程遥控手术操作。在这里只考虑运动跟踪问题，叠加运动作为以后研究的内容。
在心脏旁路移植手术中，冠状动脉血管的直径范围为0.5~2.0 mm。为了保证手术安全，动态误差应保持在血管直径的1%以内，即对于高频带心脏运动的动态跟踪误差要保持在小于100 μm的范围内。在以往的研究中，NAKAMURA Y[3]等人使用了反馈控制方法；OORTMAIER T[4]等人提出基于Taken原理心脏运动预测方法的控制方法；GINHOUX R[5]等人提出广义模型预测控制器；DUINDAM V和SASTRY S[6]提出基于模型的渐进控制算法。参考文献[7]提出心脏运动信号的自适应时变线性回归模型，将心脏信号跟踪问题转化为基于心脏运动信号模型的运动跟随问题，并应用最优跟踪理论，实现了基于心脏运动模型的随动跟踪控制。以往的研究结果表明,基于模型的预测控制算法是解决心脏手术辅助机器人跟踪控制问题的有效方法，其优点是对心脏未来运动的预测增加了系统的带宽，让控制器超前对心脏运动的位置做出判断进而准确跟踪。
本文提出了一种基于位置与加速度信号的耦合模型的多步模型预测控制方法。该方法的优势表现在：(1)增加了对机器人端点的3D加速度测量，因为加速度是位移的二阶导数，所以在一定程度上扩大了加速度的测量系统的带宽；多传感测量信息经过卡尔曼滤波器的融合处理为控制器提供了更多的超前运动信息。(2)心脏运动时变模型提供超前并非单步的，而是N步的参考输入，这样的做法同样扩大了系统的带宽。
1 手术辅助机器人耦合模型
图1是PHANToM实验平台的坐标系统和初始位置示意图。其中小写的x-y-z代表基准空间坐标系，大写的X-Y-Z代表工作空间的坐标系,为了计算方便选取两者重合。
机器人系统的动态模型用质量-弹簧-阻尼物理系统来近似，因为机器人实验平台端点可以在3D空间中自由运动，因此可以得到3个彼此独立并且结构相近的物理模型。在此首先要研究一下3D机器人实验平台在笛卡尔坐标系下的X轴运动方向上的状态变量。图2展示了带有加速度测量与位置测量的PHANToM实验平台的x轴质量-阻尼-弹簧近似物理模型[8]。
选择状态变量：
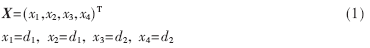
其中d1是M1的位移，d2是M2的位移，因此模型的状态空间表达为:
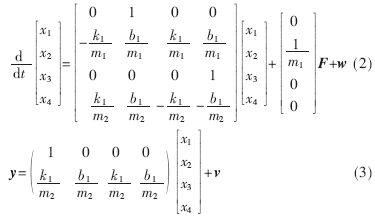
其中b1为扭转粘性摩擦参数,k1为弹簧系数,F为施加在m1的外部作用力,w为过程噪声向量,v为测量噪声向量。通过式(3)可以看出m的加速度是状态变量的线性组合。其优势在于当得到了加速度测量值，将加速度测量值和位置测量值用来作状态估计比单独的位置测量值能够对系统状态提供更有效的估计，进而提高机器人动态跟踪性能。由式(2)、式(3)位移-转矩和加速度-转矩的传递函数分别由式(4)、式(5)所示：
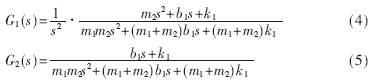
以上两个带参数模型有部分相同的参数，是两个相互耦合的模型。当得到输入输出数据的离散傅里叶变换后，便可以利用非线性最优化的方法来确定两个传递函数的参数。
2 手术辅助机器人的控制算法
控制算法是整个手术辅助机器人跟踪控制的核心。心脏表面的手术操作点的运动幅度高达12 mm，最高运动频率高达26 Hz。基于心脏运动信号的分析，心脏表面某点存在两种运动模式，分别是1 Hz以下的呼吸运动主导的运动及2 Hz心脏运动主导的心跳运动。呼吸运动的跟踪仅仅可以通过反馈控制器来完成，而心跳运动则要通过前馈控制器来超前消除。前馈控制器需要知道心脏运动值的超前信息来相应地做出补偿，因此应用模型预测控制首先要得到心脏运动的N步预测值，将其作为模型预测控制器的参考输入，基于耦合模型的预测控制器得到位置与加速度测量值，运算得到的机器人输出控制率的前馈部分和反馈部分便分别满足对心脏运动两个主导模式的跟踪控制。
2.1 基于心脏运动时变模型的N步预测
参数时变模型来模拟心脏运动表示为：
只受过程白噪声干扰的随机漫步过程。定义测量值h(t)=y(t)，时变参数傅里叶级数模型的状态空间表示为：
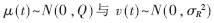分别为模型噪声与测量噪声。噪声默认为白噪声。对于心脏未来运动信号的预测需要通过估计模型中的状态来解决。考虑到测量方程为非线性方程，扩展卡尔曼滤波器可以用来估计时变的状态参数。首先将非线性的测量方程在当前的状态点
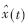线性化得到测量矩阵C：
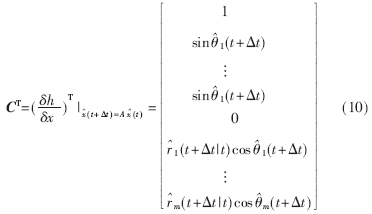
接着按照卡尔曼滤波的递推方程估计下一个时间的状态。递推方程表述为：
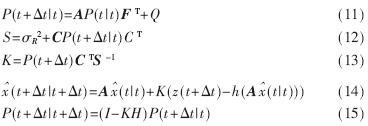
其中P为状态估计均方值。利用上述递推方程便可得到模型预测控制所需的心脏运动N步超前预测值：
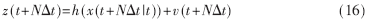
2.2 基于耦合模型的机器人模型预测控制算法
模型预测控制的原理框图如图3表示。与传统预测控制的不同之处是将状态观测器改进为基于耦合模型的卡尔曼滤波器来对机器人运动状态的估计。同时保留前馈通路的控制率输出。在应用卡尔曼滤波器作状态估计的过程中，卡尔曼滤波器会考虑耦合模型的过程误差和传感器的测量误差模型作为设计参数包含于整个算法之中。这样得到状态估计优于一般的状态观测器。因此，基于耦合模型的预测控制问题可以描述为：已知未来N步参考输入值，应用最优化的方法求解目标方程，其中机器人耦合模型作为目标方程的约束条件，求解出未来N步控制率输出，仅选取当前点传送给机器人。以下为推导过程。
机器人耦合动态模型为：
这里定义N步预测值为向量yest[k]，k0<k<k0+T指在时间k0与k0+T之间的采样时间。机器人的位置输出逼近信号yest[k]，则最优控制目标方程为：
改进的预测控制中，式(27)中的x[k]由卡尔曼滤波器的输出替代。每个控制周期中，心脏运动时变信号模型提供超前N步的心脏运动估计值传递给控制器作为参考值，控制器跟踪参考值按照上述公式计算出前馈与反馈输出率。
3 实验和结果
3.1 实验平台
控制算法通过实验平台PHANToM Premium 1.5A实现。3D加速度传感器使用是Freescale MMA7340L。在实验设置中，控制算法运行在2.6 GHz Intel Pentium4 PC 上Matlab xPC Target v2.8实时内核中。计算机控制系统的采样频率为0.5 ms。在每次试验前，先校准机器人。机器人的端点从系统初始位置开始跟踪信号。在实验中，预先采集的心脏信号用于模拟实际的非体外循环手术中心脏在每个采样时刻跳动位置的数值。
3.2 实验结果及讨论
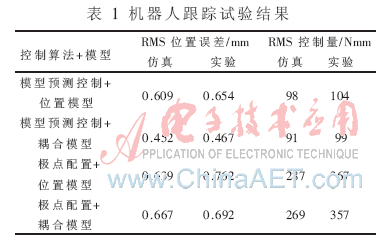
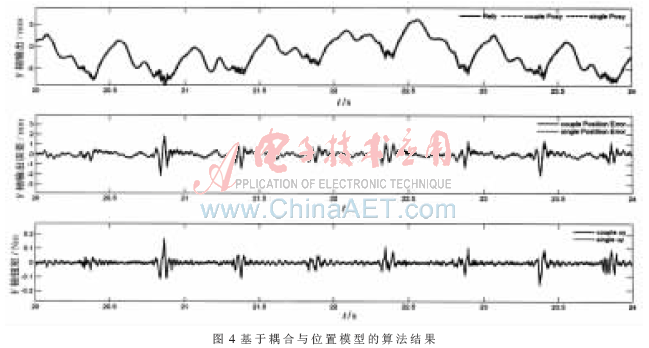
实验对比了模型预测控制器与极点配置控制器分别在单独位置测量模型与耦合模型的情况下对心脏的运动跟踪。通过对算法结果比较得出基于耦合模型的多步预测控制算法在两方面优于其他控制算法：(1)增加加速度测量的耦合模型预测控制增加了系统带宽，对所跟踪的信号具有超前补偿能力。(2)多步预测增强了基于耦合模型的多步预测控制算法对于心跳信号快速变化的估计与跟踪能力，进而提高控制精度。表1总结了实验得到的RMS跟踪误差与RMS控制量输出。图4展示了在耦合模型与单独位置模型的预测控制算法下，机器人端点工作空间坐标系中X轴位置、跟踪误差与控制量输出。图中分别用不同的时间尺度表现两个模型对应的算法的优劣。
本文中提出了基于速度与加速度测量的耦合模型的改进预测控制算法。在耦合模型的算法结构下，通过增加加速度传感器对机器人端点运动的测量提高了跟踪精度。模型预测控制器按照心脏运动信号的特点分别对心脏运动中高频与低频分量分离出前馈控制率与反馈控制率，前馈部分的引入克服了测量在反馈环节产生滞后性。
本文结论如下：(1)模型预测控制算法具有超前预测的属性。将信号跟踪问题归结为参考信号预测问题，是算法前馈控制部分的必要基础。通过提高模型预测的精度实现提高跟踪控制的精度，为高带宽高精度的信号跟踪提供了可能。(2)包含了加速度信号测量信息的耦合模型，具备由于仅位置测量的超前相位的特征，提高了机器人对高带宽信号的准确跟踪能力。试验结果表明本文提出的带有加速度测量耦合模型跟踪算法比现有的位置测量算法的跟踪误差减小至少20%。
参考文献
[1] NEWMAN M F,KIRCHNER J L,PHILLIPS-BUTE B,et al.Longitudinal assessment of neurocognitive function after coronary-artery bypass surgery [J]. New England J Med.,2001,6(344):395-402.
[2] FALK V. Manual control and tracking-A human factr analysis relevant for beating heart sugery[J].Thoracic Surg,2002,74:624-628.
[3] NAKAMURA Y, KISHI K,KAWAKAMI H. Heartbeat synchronization for robotic cardiac surgery[C]. in Proc.of IEEE International Conference on Robotics and Automation(ICRA),Seoul, Korea, May 2001,2. 2014-2019.
[4] ORTMAIER T, GROGER M, BOEHM D H, et al. Motion estimation in beating heart surgery[J]. IEEE Transactions on Biomedical Engineering, October 2005,52(10):1729-1740.
[5] GINHOUX R, GANGLOFF J A, DEMATHELIN M F,et al.Active filtering of physiological motion in robotized surgery using predictive control[J]. IEEE Transactions on Robotics, 2005,21(1):67-79.
[6] DUINDAM V, SASTRY S. Motion estimation and control for roboticassisted beating-heart surgery[C]. in Proc.of IEEE/RSJ International Conference on Intelligent Robots and Systems,San Diego,CA,USA,October-November 2007:871-876.
[7] 梁帆，孟晓风，董登峰.心脏动脉旁路手术中手术辅助机器人的模型跟随控制[J]. 光学精密工程, 2012,20(1): 131-139
[8] MURAT CENK CAVUSOGLU DAVID FEYGIN and FRANK TENDICK. A Critical Study of the Mechanical and Electrical Properties of the PHANToM Haptic Interface and Improvements for High-Performance Control[J]. 2002,11(6): 555-568.
[9] ANDERSON B D, MOORE J B. Optimal control linear quadratic methods[M]. Englewood Cliffs, NJ: Prentice-Hall,1990.