摘 要: 基于对无标记数据算法的研究,讨论了基因数据分析的半监督学习算法。基因数据的典型特征是小样本、高维数,处理起来非常困难。在安全的半监督学习基础上,提出了一种降维和半监督学习相结合的方法,以提高分类效果的精确度及鲁棒性。实验证明,该方法通过结合降维和半监督学习的优点,具有很好的应用价值。
基因芯片技术可以一次性对大量基因序列进行检测和分析,从而得到高维的基因表达数据,因此在病理研究和临床应用等领域备受关注[1-2]。基因表达数据中基因的数目巨大,大部分都无法为样本的区分提供有用信息,因此识别出一小部分能提供足够有用信息的基因并实现很好的分类至关重要,这一小部分有效基因被称为分类特征基因。特征基因选择通常由去除分类无关基因和去除冗余基因两部分组成。GOLUB T R等人提出的特征记分准则FSC(Feature Score Criterion)用于去除分类无关基因[3]。李颖新等人[4]认为应该在此基础上考虑方差对样本分类的影响,利用方差不同对样本分类的贡献不同,从而更客观地评价基因包含的分类信息量,提出了修订的特征记分准则RFSC(Revised Feature Score Criterion)。关于特征基因的选择研究有过滤法、缠绕法、混合方法等[5-6]。特征基因选择之后,选出的剩余基因可以看作与疾病相关。因为利用基因数据的高维数和高噪音进行特征提取是必要的途径。本文结合降维技术方法给出新的特征提取方法。提取特征后,样本的分类又显得尤为重要,一个好的分类器能够更准确、更有效地区分正常样本,从而为临床医学提供参照。半监督学习(Semi-supervised Learning)是目前比较有效的分类方法[7],它主要考虑如何利用少量的标注样本和大量的未标注样本进行训练和分类的问题。本文提出的降维和半监督学习方法能够更好地利用数据的隐含信息,更好地实现分类预测效果。
1 数据描述及标准化
1.1 基因表达数据
基因表达谱数据可以表述为:
M=x11 x12 … x1n c1x21 x22 … x2n c2 ?埙xm1 xm2 … xmn cm (1)
肿瘤基因表达谱M中共有m个样本、n个基因。xij代表第i个样本的第j个基因表达值; ci代表样本所属类别。gi为第i个基因所有样本的表达值,简称为基因gi:
gi=x1ix2ixmi (2)
基因表达谱最显著特点是样本少、维数高,即m<<n[2]。
1.2 基因表达数据标准化
对基因表达数据进行标准化的方法主要有两种:(1) 限制每个基因的均值为0,方差为1;(2)限制每个基因的值在[0,1]范围内。
本文采用限制每个基因的值在[0,1]范围内的标准化方法:
xij*=(xij-xj-max-xj-min)
其中,xij为式(1)中所示的基因表达矩阵M中第i个样本的第j个基因,xj-max为第j列基因的最大值,xj-min为第j列基因的最小值,xij*为标准化后的新值。
2 数据处理的相关理论方法
2.1 IRFSC特征计分准则
由于相关组织的某些基因发生了突变,而突变基因的表达水平与正常基因的表达水平不一样,因此,需要找出突变基因。原则是:将患病和正常样本两类中具有显著差异的基因子集保留,其余视为无关基因去除。通常是按照某种记分准则对每一个基因进行记分[6],分值越大说明该基因的正常样本和肿瘤样本差异越大、基因含有的分类信息就越多。因此按基因分值大小降序排列,排在前面一定数量的基因作为候选基因,其余基因作为无关基因去除。参考文献[5]中对GOLUB T R等人提出的FSC进行改进后为:
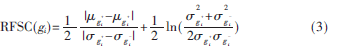
若基因表达谱中只有正常样本和肿瘤样本两类,则表示基因gi中正常样本的均值,表示gi中肿瘤样本的均值;表示gi中正常样本的标准差,表示gi中肿瘤样本的标准差。考虑到样本数目m和基因数目n之间的大小关系m<<n[2],由于n/m的比值越大,对方差的影响也越大,给出式(3)的改进形式:
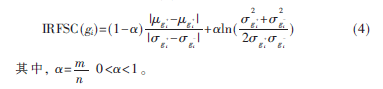
2.2 降维方法
2.2.1 主成分分析
主成分分析PCA(Principal Component Analysis)算法是一个经典的统计技术,把数据从高维的空间中映射到低维的空间并保留主要的信息[8]。在新的坐标系下,变换数据点的方差沿新的坐标轴得到了最大化,这些坐标轴经常被称为主成分。PCA的主要运算步骤如下:

2.2.2 局部保持投影
局部保持投影LPP(Locality Preserving Projection)是一种线形的降维算法[9]。LPP的目的是保持局部的结构信息,所以在低维空间的近邻搜索与高维空间产生类似的结果。LPP是线性的,这使得LPP处理速度很快,并且很适合于实际的应用,这也是LPP优于LLE的地方。降维后产生的变换矩阵可以直接应用在测试集上,所以,其拥有样本外点学习能力。
LPP的算法如下:
(1)PCA投影。通过保留主要成分,将数据集投影到子空间。
(2)构建邻近图。如果样本点Xi和样本点Xj是近邻点,则可以在Xi和Xj之间建立一条边。建立的近邻图是局部流形结构的近似,常采用K近邻方法。
(3)如果样本点i和j相连,则设置权重W=e,其中t是一个合适的常数;否则W=0。
其中,L=D-W,而对角矩阵D的对角线元素Dii=Wij。
(4)本征映射。计算特征值分解问题:XLXT?琢=?姿XXT?琢求解广义特征方程的d个最小特征值对应的特征向量作为d个投影向量。故由上述特征方程的d个最小特征值?姿1,?姿2,…,?姿d对应特征向量?琢1,?琢2,…,?琢d,构成保持近邻重建特性的线性变换矩阵。
2.3 支持向量机
支持向量机SVM(Support Vector Machines)是由VAPNIK提出的一种新的机器学习方法[10],它基于VC维和结构风险最小化理论 (SRM),在很大程度上解决了传统机器学习中的维数灾难及局部极小等问题。由于其完整的理论框架和在实际应用中取得了很多好的效果,在机器学习领域受到了广泛的重视,图1给出了SVM分类的示意图。

当给定的训练样本集为{xi,yi},其中i=1,…,N,相应的类标签为yi={-1,+1}。在线性可分的情况下,SVM 能找到一个能使两类样本集分类间隔最大的最优超平面。这等价于解决下面的规划问题:
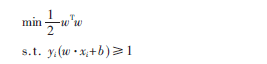
由于支持向量机是利用有效的少量样本去构建超平面来预测测试样本,支持向量的选择对分类器的精度影响很大。对大量的数据样本进行处理,分类器的精度变化不会很大;但是对于少量的样本进行处理,分类器精度的变化会非常明显,尤其是遇到高维小样本问题。分类器的精度如果变化很大,就在实际应用中就会带来意想不到的后果。鉴于基因数据的特点(高维数和高噪音),把最新的支持向量机S4VM应用到本文的算法中。S4VM是对S3VM的改进,后者主要关注一个最优的低密度分界线,而S4VM同时关注多个可能的低密度分界线。因为给定一些有标记的点和大量为标记的点,可能存在不止一个低密度分界线,所以很难决定哪个是最好的,如图2所示。虽然这些低密度分界线都与有限的标记样本吻合,但它们之间的差异很大,因此如果选错了,会有一个很大的损失,导致性能的下降。所以,S4VM试图考虑所有可能的低密度分界线。在给定许多不同“间隔”较大的分界线时,通过对未标记的样本的类别划分进行优化,使得在最坏的情况下,相对于只使用标记样本的支持向量机的性能提升最大化。

3 算法流程
本文提出算法的具体流程如下。
(1)对肿瘤基因表达谱进行标准化。
(2)去除无关基因。利用RFSC计算每个基因的分值,
经过降序排列后选出分值靠前的一部分基因作为候选基因。
(3)特征提取。利用局部保持投影提取主要的特征。
(4)分类测试。利用S4VM进行分类精确度的检验。
4 实验结果及讨论
采用肿瘤基因表达数据集(http://home.ccr.cancer.gov/ oncology/oncogenomics/)进行实验测试,该表达谱共27个样本(其中16个为正常样本,11个为肿瘤样本),3 467个基因。然后,采用ALON等人[11]选出的含有2 000个特征基因的结肠癌基因表达谱数据集,包括40个结肠癌组织样本和22个正常样本进行降维实验对比。
实验1 选取数据集中的27个样本,采用SVM和S4VM进行分类精度检验,分别选取分类信息指数为0.5、0.7、0.8、0.85、0.9的2 085、819、417、279和184个基因。SVM选取1/10、3/10、5/10、7/10、8/10作为训练集;S4VM选取1/10、3/10、5/10、7/10、8/10作为有标号的数据。实验对比结果如表1所示。
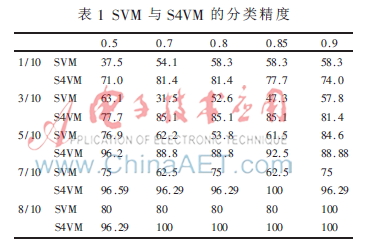
在此实验中,训练集的样本数越多,分类效果越好;对于S4VM,有标记的样本数越多,其精确度越高,而且可以看出S4VM不会出现太大的精度变化,而SVM精度变化很大,说明S4VM的鲁棒性效果非常好。
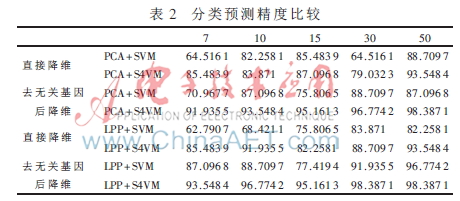
实验2 进行去无关基因和直接降维的对比。采用了PCA+SVM、PCA+S4VM、LPP+SVM及LPP+S4VM进行了对比实验;选择315个特征基因分别降到7、10、15、30、和50维。采用SVM分类器时作为训练集,在用S4VM时采用62个样本中的3/10约 19个作为标记的数据。实验对比结果如表2所示。可以得出,无关基因作为样本中无关的属性,其存在对分类器模型的选取影响很大;LPP由于很好地保持了局部结构,其降维效果明显要比PCA好;S4VM由于考虑了多个低密度分割器,并且充分利用了无标记的数据,使其对分类器的训练有更好的贡献,其鲁棒性及精度要比直接使用标记数据的SVM分类效果更明显。
基因数据的主要特点是高维数和高噪音。本文基于挖掘数据本质特征的思路,采用降维和安全的机器学习技术提出一种基因数据分析的半监督学习算法。通过实验证明了算法中应用降维的有效作用,同时也显示出应用S4VM作为学习机的潜力,为该方面更深入的研究提供了重要理论和方法基础。
参考文献
[1] HOUBIN B, CHUNG R. Gene expression data classificationand Bioengineering(BIBE), IEEE 11th Inter-national Conference, 2011:66-71.
[2] YEUNG K Y, RUZZO W L. Principal component analysis for clustering gene expression data[J]. Bioinformatics, 2011,7(9):763-774.
[3] GOLUB T R, SLONIM D K, TAMAYO P, et al. Molecularclassification of cancer: class discovery and class predic-tion by gene expression monitoring[J]. Science, 1999(286):531-537.
[4] 李颖新,李建更,阮晓刚.肿瘤基因表达谱分类特征基因选取问题及分析方法研究[J].计算机学报,2006,29(2):324-330.
[5] 于化龙,顾国昌,赵靖,等. 基于DNA微阵列数据的癌症分类问题研究进展[J]. 计算机科学,2010,37(10):16-22.
[6] 张敏,戈文航.双聚类的研究与进展[J]. 微型机与应用,2012,31(4):4-6.
[7] HUANG S C, WU T K. Robust semi-super-vised SVM on kernel partial least discriminantspace for high dimensional data mining[C]. Proceedings of Information Science and Appli-cations(ICISA), International Conference,2012:1-6.
[8] JOLLIFFE T. Principal component analysis [M].New York:Springer,1986.
[9] He Xiaofei,NIYOGI P.Locality preserving pro-jections[C]. Proceedings of Advances In Neural Information Processing Systems 16, MA: Cambridge, MIT Press, 2004:153-160.
[10] Li Yufeng, Zhou Zhihua. Towards making unlabeled data never hurt[C]. In: Proceedings of the 28th International Conference on Machine Learning(ICML’11), Bellevue, WA, 2011:1081-1088.
[11] ALON U, BARKAL N, NOTTERMAN D A, et al. Broad patterns of gene expression revealed by clustering analysisof tumorand normal colon tissues by oligonucleotide arr-ays[J]. Proceedings of the National Academy of Science, 1999,96(12):6745-6750.

