摘 要: 对EEG脑电信号的有效处理和分析,可以判断不同的脑机能状态,在神经生理科学研究和临床诊断中有着广泛应用。考虑到EEG脑电信号中每个单独的生物信号时间上的相关性和不同信道生物信号之间的信道间相关性,基于离散余弦变换基对EEG脑电信号进行稀疏化,并利用基于块稀疏贝叶斯的压缩传感技术对其进行仿真重构。大量实验结果表明,重构的EEG脑电信号与原信号具有极大的相似保真度,能够用于医学上的进一步处理。
0 引言
脑电信号是脑细胞群发出的微弱生物电,可利用放置在头皮或颅内的电极检测并记录下来,是一种反映大脑生物电节律性活动规律的随机非平稳信号,在临床诊断和脑功能研究方面具有十分重要的参考价值[1]。由于脑电信号数据的庞杂性,如何在压缩脑电数据,有效减少其数据量的同时,保证其主要特征基本不变,并能够通过高质量重构还原脑电波形,实现对脑电信号的准确分析,是一项很有意义的研究工作。
稀疏贝叶斯学习(Sparse Bayesian Learning, SBL)最初作为一种机器学习算法由 Tipping于2001 年前后提出[2],随后被引入到稀疏信号恢复/压缩感知领域[3]。作为一种贝叶斯算法,SBL 算法对利用这些解的结构信息提供了更多的灵活性。这种灵活性最主要来自于SBL采用参数化的高斯分布为解的先验分布。采用基于块稀疏贝叶斯学习框架的算法[4-5]对脑电信号进行压缩采样能实现信号的高质量重构。实验证明此方法能够有效地重构脑电信号,便于后续的一系列医学分析,对促进脑电医疗设备的改良具有实际意义。
1 块稀疏贝叶斯压缩感知基本理论
1.1 传统压缩感知基本原理
压缩感知的基本模型可描述为:

其中,A为N×M的感知矩阵,y为N×1维压缩信号, x为M维待求的解向量,v为未知的噪声向量。为求解x,SBL假设x中的每个元素都服从一个参数化的均值为0方差为γi的高斯分布[3]:

其中,xi表示x中的第i个元素,γi是未知参数,将由算法自动估算得出。在算法运行过程中,绝大部分的γi将会变成0(无噪情况下)或者趋于0(有噪情况下)。SBL通常会采用一个阈值将趋近于0的γi置为0(该阈值的大小通常与信噪比有关)。当γi=0时,相应的xi为0。因此,γi与解的稀疏程度密切相关。在SBL框架中,噪声v通常假设为高斯白噪声向量,即missing image file,其中λ为噪声方差。Wipf和Rao已从理论上证明,这种SBL框架可以获得真正的解(即最稀疏的解)[3]。
1.2 块稀疏贝叶斯理论
式(1)中解向量x最常见的结构是块结构(block structure),或称为组群结构(group structure)[6-7],即:
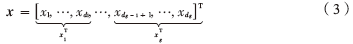
基于这个块划分的基本压缩感知模型(即公式(1)、(3))称为块稀疏模型(Block Sparse Model)。在这个模型中,解向量x可以划分为g个块结构(每个块结构包含的元素有多有少),而x的非零的元素则聚集在少数几个块内。但目前很少有算法考虑每个块内的元素之间的相关性(幅值的相关性),即块内相关性。块内相关性对算法性能的影响直到最近才被Zhang和Rao通过提出块稀疏贝叶斯学习(Block Sparse Bayesian Learning, BSBL)而发现[5],并被成功运用到非稀疏生理信号的无线传输[5,8]。
在BSBL(Block Sparse Bayesian Learning)中,每一个块被假设为满足一个多元高斯分布:

其中,Bi为一未知的正定矩阵,用于对该块内的元素之间的相关结构进行建模,而γi为一未知的参数,用于决定该块是否为0。类似于基本的SBL框架,当γi=0时,相应的块xi=0。由于ARD(Automatic Relevance Determination)机制在算法学习过程中大多数γi最终为0或者趋近于0,从而促成了解的块稀疏性(Block Sparsity)。同样,假设噪声服从missing image file,这样就可以利用贝叶斯规则得到x的后验分布。利用第二类最大似然估计可以估计出各种参数,从而最终得到x的最大后验估计值。
1.3 基于块稀疏贝叶斯算法的脑电信号处理
参考文献[9]已证明了BSBL算法的重构质量相较于M-FOCUSS、SOMP等算法具有明显优势,本文测试在不同的感知矩阵下BSBL算法对脑电信号的重构质量,这里分别使用随机二进制矩阵、高斯随机矩阵和伯努利随机矩阵进行测试。实验步骤如下:
⑴通过离散余弦变换基对输入信号进行稀疏化;
⑵设定信道数和迭代次数,设定块分区尺寸、块起始位置、噪声参数、学习类型、迭代最大值、容错度等参数,得到重构信号并求出重构信号的多尺度熵、结构相似性等参数;
⑶将迭代计算中生成的各个参数保存为mat文件以便于以后查阅;
⑷改变感知矩阵,重复步骤⑵和⑶。
2 仿真实验
本实验从MIT-BIH数据库下载一组正常脑电信号数据,在MATLAB中对信号进行处理。本实验过程中,感知矩阵行数M=192,列数N=384(其中二进制随机矩阵每列固定18个“1”),迭代次数ep=80,信道数ch=1。采用384×80的数据量,读入原始脑电信号,如图1所示。分别采用随机二进制矩阵、高斯随机矩阵、伯努利随机矩阵作为传感矩阵,得到重构信号如图2~图4所示。
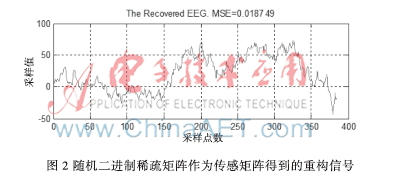


由于感知矩阵都是随机矩阵,因此每次运行结果并不完全相同,为得到精确的实验结果,重复运行程序多次,得到采用不同感知矩阵的重构结果折线图如图5所示。
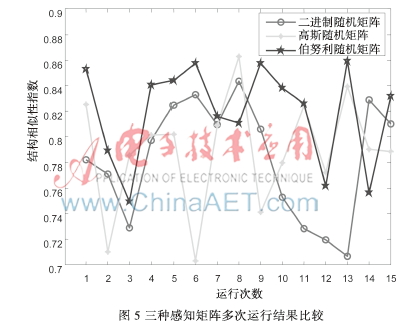
由图5可以看出,虽然每次运行结果都略有不同,但重构信号与原信号的结构相似性指数都在70%以上,还原度较高。相比较之下,采用二进制随机矩阵的重构质量抖动较大且平均值为三者之中最低;采用伯努利随机矩阵则将重构信号与原信号的结构相似性指数的值保持在75%以上,抖动较小重构质量更有保证;采用高斯随机矩阵,虽结果抖动较大但平均重构质量介于其余两者之间。

图6所示为采用随机二进制稀疏矩阵还原另一组EEG信号的效果图,同样采用384×80的数据量。
此次实验的结构相似性指数高达0.986 8,由画圈区域分析得出,块稀疏贝叶斯算法能够重构生理信号中接近为零的成分,便于进行医学方面的进一步分析。
3 结论
基于块稀疏的贝叶斯算法利用解的块内相关性能够以极高的质量恢复非稀疏信号,与目前存在的其他压缩感知算法相比,它不仅利用生物信号时间上的相关性,而且可以利用来自不同信道的生物信号的空间相关性,相比较而言,具有最佳的恢复性能和恢复速度。由图2~图5得出,对于BSBL-BO重构算法,无论采用何种感知矩阵,它仍旧能够保证对原始信号高质量的还原,且相比较而言,采用伯努利随机矩阵作为感知矩阵时,信号的重构质量更有保证。图6证明了块稀疏贝叶斯算法对微弱脑电信号的重构能力,指明了下一步的研究方向,即找到能够保留原始脑电信号最大可用信息量所需要的最小采样密度,以达到用最小成本获取患者脑电信息的目的,为进一步的医学研究奠定基础。
参考文献
[1] ubeyli E D. Features extracted by eigenbector methods for detecting variability of EEG signals[J]. Patten Recognition Letters, 2008,28(15):592-603.
[2] Tipping M E. Sparse Bayesian learning and the relevance vector machine [J]. Journal of Machine Learning Research, 2001(1): 211-244.
[3] Wipf D P, Rao B D. Sparse Bayesian learning for basis selection [J]. IEEE Trans. on Signal Processing, 2004, 52(8): 2153-2164.
[4] Zhang Zhilin, Rao B D. Sparse signal recovery with temporally correlated source vectors using sparse Bayesian learning [J]. IEEE Journal of Selected Topics in Signal Processing, 2011, 5(5): 912-926.
[5] Zhang Zhilin, Rao B D. Extension of SBL algorithms for the recovery of block sparse signals with intra-block correlation [J]. IEEE Transactions on Signal Processing, 2013,61(8):2009-2015.
[6] Yuan Ming, Lin Yi. Model selection and estimation in regression with grouped variables [J]. Journal of Royal Statistical Society, 2006, 68: 49-67.
[7] Baraniuk R G, Cevher V, Duarte M F, et al. Model-based compressive sensing [J]. IEEE Trans. on Information Theory, 2010, 56(4): 1982-2001.
[8] Zhang Zhilin, Jung T P, Makeig S, et al. Compressed sensing for energy-efficient wireless telemonitoring of noninvasive fetal ECG via block sparse bayesian learning[J]. IEEE Trans. on Biomedical Engineering, 2013,60(2):300-309.
[9] Zhang Zhilin, Jung T P, Makeig S, et al. Compressed sensing of EEG for wireless telemonitoring with low energy consumption and inexpensive hardware[J]. IEEE Trans. on Biomedical Engineering, 2013, 60(1):221-224.

