摘 要: 在虚拟网络环境中,提出了基于效用的链路资源分配模型,使链路资源在存在拥塞的情况下达到最优分配。模型设计了单寡头垄断情况下虚拟业务提供用户与垄断者的效用函数,以及其达到均衡的条件,同时增加寡头数来讨论企业进入条件以及资源最优分配下的企业数量。由仿真分析可以得出,基于效用的资源分配模型能够有效地促进用户与企业之间、企业与企业之间的博弈,在双方利益最大化基础上实现资源最优分配。
关键词: 虚拟化;资源分配;效用
0 引言
互联网的迅猛发展引领了信息社会的发展,推动经济不断进步,互联网规模不断扩张的同时也面临着瓶颈,主要表现在网络中大量高带宽应用对带宽的要求,使得有限的网络资源无法满足需求;实时多媒体对网络带宽和延时要求让尽力而为的路由协议无法保证服务质量[1]。现有方案对网络模型的完善是基于具体问题上的局部性调整,这使得现有互联网成为了一个层、技术的混合堆砌模型,从而导致互联网僵化[2]。为了提高互联网网络资源利用效率,保证业务竞争和业务的多样性,网络虚拟化[3-4]势在必行。
目前,网络虚拟化的研究主要关注于虚拟化网络平台的映射及实现问题[5],而用户与业务提供者之间的效用以及内在交互问题没有得到系统的理解和分析。参考文献[6]利用博弈理论分析了网络带宽资源的分配问题,但其没有涉及定价策略。参考文献[7]针对网络资源定价分配问题提出了一个初步的理论性框架,通过博弈理论来分析拥塞网络中不同垄断者之间的交互过程以及不同价格下的分配情况。本文主要基于用户与业务提供者之间的具体交互过程,结合经济学相关理论[8-9],在双方效用最大化的基础上提出一个价格制定机制,从而分析垄断情况下的均衡价格制定策略以及寡头竞争情况下的市场进入与寡头价格制定策略。
本文首先提出虚拟网络资源分配的分层模型,然后提出了基于效用的虚拟网络资源分配及定价策略,最后进行仿真分析。
1 虚拟网络模型结构
本节主要介绍虚拟环境下的基本模型结构。在网络虚拟化环境中,网络资源主要包括节点、链路、接口等[10]。为了方便分析,本文主要以链路带宽作为网络资源来分析不同链路的流量情况。
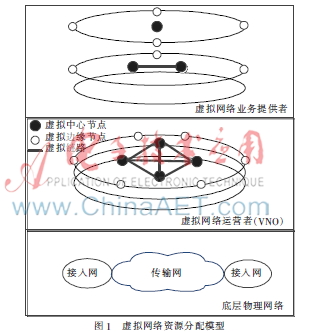
在虚拟网络环境中,本文将传统的网络服务提供商分为3个部分,如图1所示。最底层是端到端的物理资源,由节点、链路等组成,主要负责部署和管理底层网络,即底层物理资源。中间层是虚拟网络运营者(Virtual Network Operator,VNO)。VNO可以看成一个虚拟资源池,该资源池是虚拟节点以及链路的集合,其中链路带宽与虚拟核心节点的内存空间均为有限值。顶层是与业务相关的虚拟网络(VN),为用户提供各种业务。
2 基于效用的虚拟网络资源分配策略
2.1 单一VNO垄断模型
单一VNO资源分配模型主要由存在拥塞状况的网络、希望利益最大化的VNO和VN业务提供用户组成。
假设VNO拥有的链路条数为I={1,2,…,I},用户数为J={1,2,…,J}。用Xji表示用户j在链路i上的数据流量,ri表示链路i上总的流量数,Xj表示用户j使用的总流量数,则有:

由于拥塞影响,链路流量的增加会引起延时增加。引入延时函数Li(ri)来表示数据在链路i上的传输延时,Pi={P1,P2,…,PI}表示链路i上每带宽的链路价格大小。
2.2 效用函数
对VN用户而言,租用链路的总效用是用户在每条链路上得到的纯效用减去因为延时和租用费产生的消耗。用uj(Xj)表示用户j由于租用链路数Xj得到的自身效用,则用户j的总效用为:

当所有用户追求总效用最大化时,存在X={X1,X2,…,XJ}为用户所选择的流量数,该流量数达到均衡。式(3)表明,每一个用户的总效用是由所有用户的流量分布决定的,用户既能决定链路的延时函数,又能决定链路的价格,因为用户不同的流量分布会改变链路负载和延时,进一步改变VNO对链路价格的制定。
对VNO而言,由于其希望得到利益最大化,因此VNO根据各条链路的流量情况制定价格,这里忽略了数据传输成本。VNO制定的价格值即为式(4)的最优化:

其中,ri(P)是链路i在价格为p的情况下达到均衡时的总流量数。
由于ri(P)是P上的连续函数,因此式(4)必然存在最优解P*。当价格为P*时,存在X*为用户选择的流量数,用(P*,X*)表示。
2.3 多VNO寡头竞争模型
当链路资源不再由一个VNO独有,而是由多个VNO共有时,VNO之间就产生竞争。假设每个潜在企业都有可能进入市场。现市场中已有一个企业IVNO(Incumbent VNO),下面讨论第一个企业EVNO(Entry VNO)进入的情况。
由于EVNO不拥有任何物理链路资源,因此当EVNO进入市场时,需要向IVNO租用物理链路资源。设λ∈[0,1]为允许EVNO与自己共用资源的程度。若λ=0,IVNO不允许EVNO使用自己的物理资源,则EVNO需要构建自己的底层资源。若λ=1,IVNO允许EVNO完全自由地使用自己的物理资源,则EVNO不需要花费另外的资金进行底层资源的构建。这里用d(λ)表示自己构建底层资源的费用,则d(λ)是一个λ的递减函数。
对于EVNO的市场进入,可以将其看成是一个三阶段博弈过程,下面从第三阶段开始讨论,然后进行逆向分析。
阶段3:竞争
如果EVNO进入市场,则根据IVNO制定的允许接入度λ∈[0,1]和启动成本,EVNO的进入成本T可以表示为T=rq2+K,其中,r为每单位链路的租赁费用,K为固定的启动成本。若在阶段1中IVNO已经确定λ和K的大小,则各企业的利润IIi具体如下:
II1(λ,r,K)=II1+K(5)
II2(λ,r,K)=II2-K-d(λ)(6)
II1=(P1-c)q1+rq2(7)
II2=(P2-c-r)q2(8)
其中,Pi为不同VNO的链路价格,qi为不同VNO的链路产量,c为每单位链路的成本。
由于企业与企业以及企业与用户之间相互博弈,因此企业之间的竞争均衡价格可以用式(9)求得:
max{II1(λ,r,K),II2(λ,r,K)}(9)
阶段2:EVNO进入决策
EVNO的进入策略为:只有在满足II2(λ,r,K)≥II2的条件下,才会选择进入。IIi表示当VNO之间不存在租赁关系时,各VNO所获得的利润,因此有II1=II(s)和II2= II(s)-d(0),其中s表示各VNO的平均产量。由式(6)可求出EVNO的进入条件II2(λ,r,K)≥II2可转化为:K≤?准(r),其中:
?准(r)=II2-d(λ)-II(s)+d(0)(10)
阶段1:IVNO准入策略
现在考虑IVNO确定λ、K和r大小的策略。IVNO的威慑存在3种情形:EVNO不进入;EVNO的进入不可避免;威慑能够阻碍但不能阻止EVNO的进入。
(1)若EVNO选择不进入,则表示启动成本K太高,进入市场竞争不值得。在这种情况下,EVNO的进入受到威慑而阻止,IVNO在市场中形成垄断。
(2)若EVNO一定要进入,则表示进入市场竞争所获得的利润远大于启动成本,IVNO的威慑不起作用。
(3)若EVNO受到一定的威慑但没有被完全阻止,则分析在给定接入度λ的情况下,IVNO需要满足条件:
maxII1(λ,r,K)=maxr,K{II1+K}
=maxr,K{(P1-c)q1+rq2+K}(11)
s.t.K≤(r),K≥0
由式(8)可知,II2是单价r的递减函数;而由式(10)可知,对于给定的λ,存在对应r(λ),使得(r)=0。当r>r(λ)时,(r)<0,反之亦然。因此,为了满足式(11)中的两个约束条件,必须有r<r(λ)。
2.4 社会福利函数
当EVNO可以自由进入时,讨论达到均衡时EVNO的数量。为了简单处理,假设EVNO一旦进入就不改变其决定,且规模产量相同。这样,当市场中的VNO数量达到均衡时,存在J个VNO的条件当且仅当:
IIJ≥K(12)
IIJ+1<K(13)
根据市场中企业进入的数量,可以得到社会福利大小,社会福利就是社会各VNO总利润与消费者剩余之和。用qJ表示J个VNO存在于市场的情况下,均衡时每个VNO的产量用P(.)表示。因此每个VNO的利润可以表示为:IIJ=P(JqJ)qJ-c(qJ),其中c(qJ)表示每个企业的成本函数,并有c(0)=0。
用马歇尔总剩余来衡量福利大小,则当市场上有J个企业时,社会福利可以表示为:
W(J)=P(s)ds-Jc(qJ)-JK(14)
当W(J 0)=0,得到整数解J 0,该J 0就是社会最优分配下的VNO数量。
3 仿真分析
根据前文提出的基于效用的资源分配策略,采用仿真实验来验证其效果。为了便于分析,实验主要假设市场中存在两个VN业务提供用户,VNO拥有4条虚拟链路资源。设效用函数为u(X)=Xa,0<a≤1;延时函数为 L(r)=rb,b≥0。仿真结果如图2和图3所示。

由图2可知,随着时间的推进,VNO最后达到均衡状态。初始价格低的链路虽然最初利用率高,但会导致长延时,用户效用低,用户转而选择其他链路。各条链路的选择情况最终处于稳定状态。而由图3用户的归一化效用变化可知,用户在不断选择链路的过程中效用不断增大,当链路选择达到稳定时,各用户和VNO也得到最大的效用。
对于多VNO进入,本文主要分析古诺竞争均衡下市场中VNO的数量。为了便于分析,将三阶段博弈中的第二阶段简化成古诺模型,即每个VNO都存在固定的单位链路成本c,c(q)=c*q,且价格函数为P(q)=a-b*q,a>c≥0,b>0。由式(14)可以得到随着数量增加时的社会福利大小。仿真结果如图4所示。
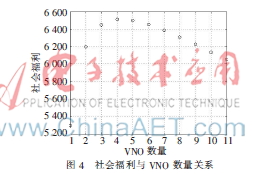
由图4可知,在不同VNO数量进入市场的情况下,社会福利的大小也不同,由此可知在给定单位链路成本c和价格函数P(q)的情况下,存在J 0使社会福利达到最大,并可以认为当市场中VNO数量为J 0时,社会资源在社会层面上到达最优分配。
4 结论
本文是将虚拟网络资源分配与经济效用相结合的一次探索。本文主要分析了拥塞网络中基于效用的虚拟网络资源分配模型。该模型所运用的资源分配思想是多个用户根据自身要求选择链路和路由方法,使其效用最大;而虚拟网络运营者则根据用户的选择实时调整定价,同时考虑多个VNO之间的竞争,使其收益最大。在模型分析过程中,分别对单个VNO的垄断情形和多个VNO的寡头竞争情形进行剖析,证明该定价策略能够在利益最大化的基础上实现资源最优分配。
参考文献
[1] KNIGHTSON K. NGN architecture: generic principles[J]. IEEE Communications Magazine,2005,43(10):49-56
[2] AOYAMA T. A new generation network: beyond the Internet and NGN[J]. IEEE Communications Magazine, 2011,47(5):82-87
[3] ANDERSON T, PETERSON L, SHENKER S, et al. Overcoming the Internet impasse through virtualization[J]. Computer, 2005,38(4):34-41
[4] 罗娟,徐岳阳,李仁发.网络虚拟化中动态资源分配算法研究[J].通信学报,2011,7(32):64-69.
[5] 杨宇,陈山枝,李昕,等.虚拟环境中基于Stackelberg博弈的资源分配[J].华中科技大学学报,2012,40(S1):311-315.
[6] Zhou Ye, Li Yong, Sun Guang, et al. Game theory based bandwidth allocation scheme for network virtualization[C]. 2010 IEEE Global Telecommunications Conference, GLOBECOM 2010, 2010:1-5
[7] 张小庆,李春林,钱琼芳,等.基于合作博弈的虚拟化资源效用分配策略[J].计算机科学,2012,6(39):51-53.
[8] 邓德传,蒋从锋,徐向华,等.虚拟机资源分配的非合作博弈标价模型[J].计算机科学,2012,39(6):380-383.
[9] 黄智兴.基于经济机制的资源管理与网络经济研究进展[J].计算机科学,2006,33(9):110-114
[10] JURNER J S, TAYLOR D E. Diversifying the Internet[C]. IEEE Global Telecommunications Conference, GLOBECOM 2005,2005,2:1-6

