0 引言

    密码设备运行算法时产生时间^[1]、功耗^[2]、电磁^[3]等边信息泄露，泄露的边信息与加密运算中的操作或数据存在相关性，利用这些边信息攻击密钥的方法叫边信道攻击。功耗分析攻击(Power Attacks，PA)^[4-5]是其中一种边信道攻击（Side Channel Attack，SCA）^[6-7]方法。攻击者采集密码设备运行时的功耗，通过对功耗信息进行分析来破解密钥。在信息安全形势日渐严峻的今天，边信道安全越来越被学术和工业界重视。

    功耗分析攻击主要分为简单功耗分析攻击(Simple Power Analysis，SPA)^[2]、差分功耗分析攻击(Differential Power Analysis，DPA)^[2]、模板攻击(Template Attack，TA)^[8]和相关功耗分析攻击(Correlation Power Analysis，CPA)^[9-10]。CPA是上述方法中对功耗信息利用较好的方法^[11-12]。然而，相关功耗分析攻击中计算相关系数相当耗时，尤其在单条功耗曲线功耗采样点过多时尤其明显，所以采用预处理技术在CPA前对功耗曲线进行压缩十分必要。

    黄永远等^[13]提出频域辅助分析的滤波方法来滤除相关性低的部分，该方法使用低通滤波后的功耗曲线所执行的攻击效率最高。《能量分析攻击》^[14]提出了最大值提取、原始整合、绝对值整合、平方和整合的方法来整合一个时钟周期内的点，达到压缩曲线的目的。

    引入主成分分析^[15]（Principal Component Analysis，PCA)到功耗分析的预处理阶段，提取功耗信息中的主要成分，抛弃次要成分，再进行相关功耗分析攻击，从而提高攻击效率。主成分分析在简单功耗分析以及模板攻击中有良好的效果，尤其是在模板攻击中。

    与模板攻击和简单功耗分析的阈值判别法不同，相关功耗分析攻击通过计算猜测值与实测值的相关性来攻击密钥。而相关性的计算对具体的数值、度量单位、密码算法的种类并不敏感，因此其应用范围以及攻击效果比模板攻击和简单功耗分析优秀。将主成分分析引入相关功耗分析攻击具有更广泛的实用意义，并以AES算法为例进行了验证。

1 经典AES算法的相关功耗分析攻击

    高级加密标准(Advanced Encryption Standard，AES)是最有代表性的分组密码加密算法，在全球广泛应用并被多方分析。因此本文以AES为研究对象。

    相关功耗分析攻击利用是实际测量功耗与其对应的操作数的汉明重量之间的相关性来破解密钥。

    详细步骤如下：

    (1)采集加密时的功耗信息得到实测功耗矩阵X。用示波器采集加密设备加密时的n(n∈N₊)条功耗曲线，每条曲线有p(p∈N₊)个功耗点。将原始数据写成矩阵形式，矩阵X每一行为一条功耗曲线，每列为按时间对齐的p个功耗采样点的值：

    (2)选择算法中间值。根据文献[14]的描述，中间值应为明文与密钥或密文与密钥的函数值。现选取AES算法第一轮轮密钥加操作后S盒的输出值为算法中间值。如图1所示，8 bit明文和8 bit密钥在执行轮密钥加异或操作之后，得到8 bit的结果，作为S盒的输入，查询S盒，得到S盒的输出。

    (3)计算假设中间值。

对可能的密钥假设k=（k₁，k₂，…，k₂₅₆），输入明文P=（P₁，P₂，…，P_n），n为明文数量，计算假设中间值矩阵V，大小为n×256。计算公式：

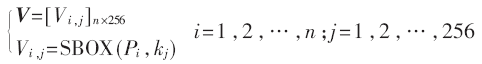
    其中，符号SBOX(P_i，k_j)为AES算法S盒替代操作函数。

    (4)将假设中间值映射为假设功耗。

汉明重量是字符串中非零的元素个数。以汉明重量模型为功耗模型，给出相关功耗分析攻击法映射的步骤，其中V为假设中间值矩阵，符号HW()表示计算输入字符串汉明重量的功能函数。计算假设功耗矩阵H公式如下：

    其每一行对应一个假设密钥。首先找出每一行最大的相关系数值，得到256个相关系数值。接着对这256个相关系数值从大到小排序，最大的相关系数值对应的密钥值(即矩阵行号)为最佳密钥候选值，次大的相关系数值对应的密钥值(即矩阵行号)为次佳候选值，以此类推。最终得到了一个字节密钥对应的256个候选密钥值。选取最佳候选密钥值为该字节密钥的猜测值。对其他算法密钥字节值都采用类似的方法进行猜测。

2 基于主成分分析的AES相关功耗分析攻击

    与经典相关功耗分析攻击不同的是：经典相关功耗分析攻击直接使用实测功耗X进行攻击，而本方法先对实测功耗X进行主成分分析预处理得到矩阵Y，再用矩阵Y进行攻击。

2.1 主成分分析

    信号处理中，主成分分析被用来提取一个混合信号中的主成分^[16]，抛弃次要成分，将复杂数据降维。它的优点是简单，无参数限制，可以方便地应用于各种场合，因此应用极其广泛。

    将原来p个指标记为X₁，X₂，…，X_p。寻求这p个变量的线性组合Y₁，Y₂，…，Y_m，(m≤p）：Y_m即为主成分分析后的主成分，用这m个主成分来表示原始数据中的大部分信息，用累积贡献率来衡量这m主成分对原始数据信息的表示程度。其满足如下性质：

    (1)主成分的方差Var(Y_i)(i=1，2，…，p)依次递减，重要性依次递减，即：

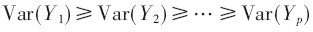
    (2)主成分之间互不相关，即无重叠的信息。协方差Cov有如下性质：

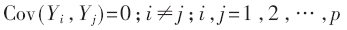
    性质(2)保证每个主成分都是不相关的，即保证每个主成分都不包含其他主成分的信息，从而保证最大化降维。性质(1)则保证能表示更多信息的成分在主成分编号中较小。

2.1.1 主成分分析功耗曲线预处理计算步骤

    将第1小节采集到n条功耗曲线，每条曲线有p个功耗点的功耗矩阵X进行预处理。步骤如下：

    T即为计算主成分的转换矩阵。

    一般取累计贡献率达85%～95%的特征值λ₁，λ₂，…，λ_m所对应的第1、第2、…、第m（m≤p）个主成分。

2.1.2 主成分的贡献率

    主成分分析的目的是减少变量的个数，所以一般不会使用所有p个主成分的，忽略一些带有较小方差的主成分将不会给总方差带来太大的影响。

    这里称为第k(k>0)个主成分Y_k的贡献率。第一主成分的贡献率最大，这表明Y₁综合原始变量X₁，X₂，…，X_p的能力最强，而Y₂，Y₃，…，Y_p的综合能力依次递减。若只取m个主成分，则称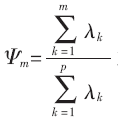为主成分Y₁，…，Y_m的累计贡献率，累计贡献率表明Y₁，…，Y_m综合X₁，X₂，…，X_p的能力。通常取m，使得累计贡献率达到一个较高的百分数，如85％以上。

2.2 实验

2.2.1 实验环境

    加密设备用Atmel ATME0A16A为硬件仿真平台，采用Tektronix DPO4032示波器采集硬件仿真平台加密随机明文时的功耗。选取AES算法第一轮S盒输出做中间值，用汉明重量做功耗模型进行相关功耗分析攻击。

2.2.2 基于主成分分析的功耗曲线预处理

    使用示波器以100 MHz采样频率采集5组样本数据，每组样本有10 000条功耗曲线，每条曲线6 700个功耗采样点。在上文硬件平台下的相关功耗攻击出全部16 B密钥需要100条左右曲线，因此样本量选择10 000能保证实验结果的稳定可靠。对5组样本分别进行主成分分析预处理，为下一步三种方案对比实验方案做准备。

    按照2.1.1节主成分分析功耗曲线预处理计算步骤进行预处理：

    (1)n=10 000条功耗曲线，每条曲线有p=6 700个功耗采集点的值，原始数据写成矩阵形式，得到矩阵X：

    每一行是一条曲线样本，每一列是对应时刻采样点的功耗值。对矩阵X进行标准化。

    (2)建立变量的协方差矩阵Cov，求协方差矩阵Cov的特征根λ₁，λ₂，…，λ_{6 700}，及相应的单位特征向量：T₁，T₂，…，T_{6 700}。求得转换矩阵T=[T₁，T₂，…，T_{6 700}]。贡献率向量L=[λ₁，λ₂，…，λ_{6 700]}。

    (3)矩阵Y=T′X，得到矩阵Y：

    矩阵Y的每一行是主成分分析处理后的一条曲线样本，每列都表示一个主成分，第一列为一号主成分，第二列为二号主成分，依次类推。

    向量L=[λ₁，λ₂，…，λ_{6 700}]，λ_p为第p号主成分的贡献率，用2.1.2节的方法计算累积贡献率曲线，把Y矩阵的每一行回写为功耗曲线的形式，预处理完成。

    预处理前的曲线示例如图2所示， 主成分分析后的曲线示例如图3所示。

    通过图3发现幅值大的功耗点都是前若干主成分，越靠后的主成分值越小并有向零趋近的趋势，结合图4累积贡献率可以发现前若干号主成分贡献率明显高于后面的主成分，该结果符合进行PCA后的理论预期。

    用2.1.2节的方法计算累积贡献率如图4所示。

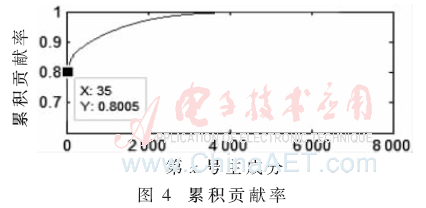
    实验结果表明，累积贡献率迅速上升到0.8即80%以上，前35号主成分就能表示全部6 700个功耗点80.05%的信息，前141号主成分累积贡献率为85.01%。多次实验显示，相关性高的主成分集中在前若干主成分中，35～141号主成分只包含5%的信息。原始采样点为6 700，为了实验对比的方便，选择前67号主成分对比实验，此时单条曲线使用的点数量为原始点数的1%。

2.2.3 对比实验

    为了验证主成分分析预处理的效果，设计3种实验方案进行对比。

    实验方案1：对原始功耗曲线进行相关功耗分析攻击，此时使用原始功耗矩阵X作为分析的功耗数据。

    实验方案2：为了找出主成分分析预处理对攻击成功率的影响，取预处理后的全部6 700号主成分进行相关功耗分析攻击，即此时使用矩阵Y作为分析的功耗数据。

    实验方案3：为了验证单条曲线使用的点数量为原始点数的1%时的攻击效果，预处理后曲线取前67号主成分进行相关功耗分析攻击，即此时使用矩阵Y的前67列作为分析的功耗数据。

    实验结果如表1、表2和表3所示。

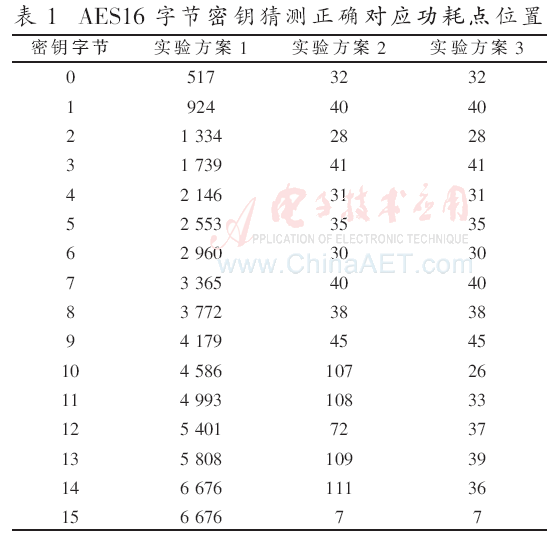
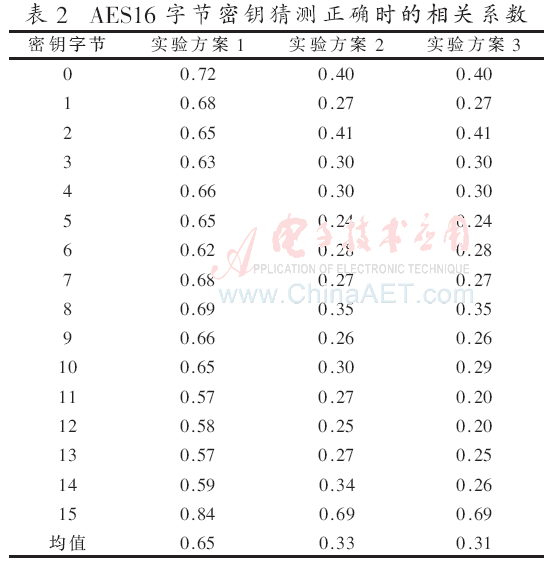
    表1中的功耗点位置表示功耗曲线中与当前字节密钥相关系数最高的点，即猜测出正确密钥的点。

    实验方案1和实验方案2对比，区别是实验2比实验1多做了主成分分析预处理。结果说明主成分分析后若是依然采用全部6 700个点进行相关功耗分析攻击，虽然都能攻击出全部16 B密钥，但是所需曲线上升至565，相关系数下降了0.32，相关性降低了。但是，中间值相关性最高的点全部在前111号主成分中，说明主成分分析有效地将信息集中到了前111号主成分。

    实验方案3和实验方案2的区别是：实验方案2使用了全部的6 700号主成分，而实验方案3只使用了前67号主成分就能恢复出全部的16 B密钥，且只用了445条曲线。再次说明主成分分析有效地把多数信息集中到了前若干主成分，主成分分析的降维效果显著。

    在2.1.1的第3步中得出第4步计算主成分时所用的转换矩阵T，在保证采样环境不变的情况下再次进行主成分分析预处理时，转换矩阵T可以作为先验知识来使用，即再次进行同样环境的功耗数据预处理时只需进行第4步。而该步骤是一个简单的线性运算，其复杂度低于计算相关系数。为了比较实验方案3和实验方案1的计算量，假设该步骤和相关系数计算花费一样的时间，由于先验知识可以预处理1 000条，取前67个主成分即可稳定破解密钥，此时处理的点数为：

    S₀=1 000×67=67 000

    相关功耗分析攻击会计算每个功耗点和中间值的相关性。设N为CPA成功时所用的功耗曲线条数，P为每条曲线的实际使用的点数，攻击程序分析的功耗点数为：S=N×P。

实验方案1分析的功耗点数为：

    S₁=60×6 700=402 000

    实验方案3分析的功耗点数为：

    S₃=445×67=29 815

    对比实验方案3和实验方案1花费的时间：

    S₁/(S₃+S₀)=4.15

    实验方案1比实验方案3多计算了4.15倍的功耗点。因此主成分分析预处理在AES的相关功耗分析攻击中是能有效的减少攻击时间的。

3 结论

    针对相关功耗分析攻击中，当功耗曲线的功耗采样点较多时攻击速度缓慢的问题，引入了基于主成分分析的预处理方法，提取功耗信息中的主成分，减少相关功耗分析攻击中分析量。引入主成分分析的相关功耗分析攻击与经典相关功耗分析攻击的对比实验结果表明，该方法可以提高攻击效率。

参考文献

[1] KOCHER P C.Timing attacks on implementations of diffie-hellman，RSA，DSS，and other systems[A].CRYPTO 1996[C].Berlin：Springer，1996：104-113.

[2] KOCHER P C，JAFFE J，JUN B.Differential power analysis[A].CRYPTO 1999[C].Berlin：Springer，1999：388-397.

[3] QUISQUATER J，SAMYDE D.Electromagnetic analysis(EMA)：measures and countermeasures for smart cards[A].E-Smart 2001[C].Berlin：Springer，2001：200-210.

[4] Mayer Sommer R．Smartly analyzing the simplicity and the power of simple power analysis on smartcards[C]．Cryptographic Hardware and Embedded Systems-CHES 2000，Springer Berlin Heidelberg，2000：78-92．

[5] NOVAK R．SPA-based adaptive chosen-ciphertext attack on RSA implementation[C]．Public Key Cryptography，Springer Berlin Heidelberg，2002：252-262．

[6] LEMKE K，PAAR C，WOLF M.Embedded security in cars[M]．New York：Springer，2006．

[7] MESSERGES T S．Securing the AES finalists against power analysis attacks[C]．Fast Software Encryption.Springer Berlin Heidelberg，2001：150-164．

[8] CHARI S，RAO J R，ROHATGI P.Template attacks[A].CHES 2002[C].Berlin：Springer，2002：13-28.

[9] PAN W，MARNANE W P．A correlation power analysis attack against tare pairing on FPGA[M]．New York：Springer，2011：340-349．

[10] 严迎建，樊海锋，徐金甫，等．针对DES密码芯片的CPA攻击仿真[J]．电子技术应用，2009(7)．

[11] KOEUNE F，STANDAERT F X．A tutorial on physical security and side-channel attacks[M]．New York：SpringerBerlin Heidelberg，2005：78-108．

[12] SEHIMMEL O，DUPLYS P，BOEH1 E，et a1．Correlation power analysis in frequency domain[J]．COSADE，2010．

[13] 黄永远，陈运，陈俊，等.运用频域辅助分析的AES算法相关功耗攻击[J].四川大学学报(自然科学版)，2014，51(3).

[14] Stefan Mangard，Elisabeth Oswald，Thomas Popp.能量分析攻击[M].北京：科学出版社，2010.

[15] 魏艳华，王丙参，田玉柱．主成分分析与因子分析的比较研究[J].天水师范学院学报，2009(2)．

[16] JOLLIFFE I T.Principal component analysis[A].ACM Computing Surveys[C].New York：Springer Verlag，1986.

[17] 张立军，袁能文.线性综合评价模型中指标标准化方法的比较与选择[J]．统计与信息论坛，2010(8).