摘 要： 针对LTE网络，在非视距传播环境下提出了一种基于层次分析法的混合定位算法以提高定位的鲁棒性。利用AOA、TDOA、PDOA得到相应测量值，利用得到的测量值分别估算出移动台的位置；再针对三种算法各自特点利用层次分析法构造对比矩阵，计算出权重向量；最后根据层次分析法进行数据融合得到移动台最后的估计位置。仿真结果表明，该基于层次分析法数据融合的移动台定位算法准确，提高了定位鲁棒性。
0 引言
随着移动通信系统向4G的迈进，无线定位在车辆的追踪、定位与导航、博物馆导览、紧急救援、导弹跟踪等领域得到广泛应用，算法鲁棒性成为一个非常重要的指标。
常采用的定位方法有到达时间差（TOA）[1]定位、时间差（TDOA）定位[2]、到达角度（AOA）[3]定位、功率差（PDOA）定位[4]及混合定位[5]。但这些算法定位波动较大，鲁棒性不理想。
因此，本文提出将层次分析法与数据融合相结合，在达到一定定位精度条件下进一步提高定位鲁棒性。层次分析法（Analytic Hierarchy Process，AHP）由美国运筹学家SAATY T L教授提出[6]，被广泛用于解决各领域的复杂决策问题[7]。本文利用基于层次分析法进行数据融合来提高算法的鲁棒性，并进行了仿真分析。
1 层次分析法
1.1 层次分析法概述
美国运筹学家SAATY T L提出了层次分析法，对方案的因素进行分层，对系统进行层次化、结构化的分析并给出决策方案。层次分析法有很好的适用性，决策的方法比较简洁。作为规划、决策和评价工具，AHP在绩效评估、方案选择等各领域有非常广泛的应用。
1.2 层次分析法步骤
（1）构造判断矩阵
层次分析法最重要的步骤就是构造判断矩阵或者权重矩阵，构造的方法一般是根据因素之间重要性程度进行比对，用比对结果来表示出两个方案的相应重要性程度等级。在决策人心中各元素重要性不一样，一般采用问卷调查法、专家意见询问法、互联网数据挖掘法等。引用1~9[8]及其倒数作为标度，得出判断矩阵A=（ai）n×n。判断矩阵标度定义如表1所示。
（2）计算权重向量
对于构造出的判断矩阵，可以求出最大特征值所对应的特征向量，然后规范化作为权值。根据判断矩阵中有用信息，采用不同的方法都可以得出其各个决策所占的权重。常用的算法有：算数平均法、特征向量法、最小二乘法、几何平均法。权重值可以为决策科学提供科学依据。
（3）一致性检验
构成的判断矩阵中的数值是由专家根据经验进行比较、问卷调查、数据挖掘等方法得出的。一般情况下判断矩阵的阶数大于2时[9]，对判断矩阵进行接受一致性的检验是保证误差在可承受范围中的一个非常重要方法，所以进行一致性检验成为层次分析法的一个必不可少的步骤。
取一致性指标（CI）与随机一致性指标值（RI）之比，并称作一致性比率（CR），即
如果CR<0.1，就认为该判断矩阵通过了一致性检验。平均随机一致性指标如图2所示。
2 TDOA/AOA/PDOA融合算法
为了使三组测量值得到充分利用，分别用时间差算法（TDOA）、角度算法（AOA）[10]和功率差算法（PDOA）[11]估算出移动台MS的位置。根据层次分析法分别算出它们所对应的权重系数，对三种算法进行融合，得出移动台最终位置坐标。TDOA、PDOA和AOA都是经典算法，这里不再赘述。
在本文的层次分析法中指标体系分为两层，融合定位算法为总目标A，第二层包括时间差定位算法B1，频率差定位算法B2，角度定位算法B3。矩阵bij表示相对于A、Bi和Bj的相对重要性。判断矩阵A-B表示相对于总目标来说，各准则之间相对重要性的比较。
本文判断矩阵采用不完全的互联网数据挖掘法，根据笔者不完全阅读无线定位文章进行随机采样，根据表1判断矩阵标度定义和采样原理得出权重矩阵如表3所示[12-13]。
CR=0.003 6<0.1通过一致性检测，故该数据有效。即加权系数为0.581 6、0.309 0、0.109 5。
设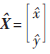
为最终移动台定位结果，
为参与定位的第i个算法的定位结果，则
=0.5816x1+0.3090x2+ 0.1095x3。
3 仿真与分析
本文的仿真是在标准蜂窝网中进行的，信道模型采用几何机构的单次反射模型，COST231NLOS传输模型采用七基站的蜂窝网，BS1为服务基站，假设蜂窝网半径为3 000 m，采用蒙特卡罗方法随机给点，模拟实际中移动台位置坐标，得到仿真结果如下。
图1为在不同小区服务半径下本文算法与其他三种算法单独定位的仿真比较结果。由图可见，随着小区半径从1 000 m增大到5 000 m，定位算法的性能均有所下降，这是由于半径的增加，BS和MS之间的距离有所增大，导致NLOS误差增加，因此定位精度也会有所下降。由图1可以看出，本文基于AHP的数据融合算法有较好的定位准确性，误差波动范围比其他三种算法都小，收敛速度快，有很好的鲁棒性。
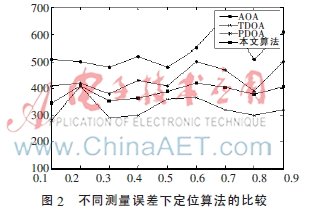
图2为不同测量误差下各定位算法的仿真结果。由图看出，随着误差的增加，本文定位算法的均方根误差最小，并且变化幅度不大，相对平稳，鲁棒性好，收敛速度快，便于以后进行跟踪；而其他三种定位算法单独定位的均方根误差较大，随测量误差的增加变化较大。这说明本文算法在一定程度上抑制了误差量的增长，提高了算法的鲁棒性，对曲线有很好的平滑作用。
4 结论
本文将层次分析法应用于无线定位算法中，该算法结合了TDOA、PDOA、AOA定位等优点，通过对三种定位算法比较得出权重矩阵进而得出权重系数，对于三种算法NLOS误差有一定修正作用，且对定位鲁棒性有很好的改善。仿真结果表明，本文算法在定位达到一定精度的基础上提高了算法鲁棒性，性能稳定、收敛速度快，与其他算法相比有较高的稳定性精度，证明了该算法的有效性和可行性。
参考文献
[1] Ma Changlin， RICHARD K， G?魪RARD L. A nonline-of-sight error-mitigation method for TOA measurements[J]. IEEE Transactions on Vehicular Technology， 2007， 56（2）： 641-651.
[2] 朱朝晖.时差定位原理及其应用[J].专题技术与工程应用，2006，36（8）：52-64.
[3] 王洪雁，兰云飞，裴炳南，等.非视距环境下基于到达时间差的一种定位算法[J].计算机仿真，2007，24（9）：116-119.
[4] 郑敏，毛永毅，杨阳.非视距传播下LTE的频率定位算法[J].电子技术应用，2014，40（2）：91-93.
[5] DIMITRIOS K， YANNIS M. Prediction in wireless networks by Markov chains[J]. IEEE Wireless Communications， 2009，16（2）：56-63.
[6] E.麦克纳，N.比奇.人力资源管理[M].丁凡，译.北京：中信出版社，1998.
[7] 秦吉，张翼鹏.现代统计信息分析技术在安全工程方面的应用——层次分析法原理[J].工业安全与防尘，1999，25（5）：44-48.
[8] 师黎，朱明杰.基于遗传算法优化BP神经网络在心电图身份识别中的应用[J].西安邮电学院学报，2008，13（3）：8069-8072.
[9] 左军.层次分析法中判断矩阵的间接给出法[J].系统工程，1988，10（6）：56-63.
[10] 毛永毅，张颖.非视距传播环境下的AOA定位跟踪算法[J].计算机应用，2011，2（31）：317-319.
[11] 董晶.LTE系统中下行信号质量RSRP测量研究[J].科技信息，2012（9）：78-80.
[12] 兰继斌，徐扬，霍良安，等.模糊层次分析法权重研究[J].系统工程理论与实践，2006（9）：108-112.
[13] 何堃.层次分析法的标度研究[J].系统工程理论与实践，1997（6）：59-61.