摘  要： 针对功率控制中存在的吞吐量受限问题，建立基于演化博弈论的功率控制吞吐量模型PCTBEGT。证明PCTBEGT模型中存在唯一的演化稳定策略并给出PCTBEGT博弈模型中网络吞吐量的定义。最后使用MATLAB工具对网络吞吐量和演化稳定策略进行实验仿真，结果表明，在使用演化博弈论的功率控制中，网络吞吐量和资源的利用率得到了进一步提高和优化。

　　关键词： 功率控制；吞吐量；演化博弈论；演化稳定策略；PCTBEGT模型

0 引言

　　无线通信中，在确保正常通话的条件下通过降低移动台或基站的发射功率来降低干扰及功率消耗，这就是功率控制。功率控制对网络的吞吐量、分组发送的实时性、网络的拓扑控制等都有很大的影响[1]。

　　目前，研究者已从工程技术角度对功率控制进行了改进和优化，然而这些改进和优化并没有考虑用户的非合作系统行为[2]，对于用户的具体行为选择也缺乏合理的解释。为此，研究人员将博弈理论引入功率控制，并取得了一些成绩[3]，包括基于博弈论的接入控制、切换策略及路由选择[4]研究等方面。

　　本文旨在研究无线网络中的功率控制问题，目的是通过演化博弈论的引入，提高网络的吞吐量，从而提高网络资源的利用率。

1 基于演化博弈的功率控制研究

　　1.1 基于演化博弈论功率控制建模

　　将基于演化博弈论的功率控制（Power Control Throughput Based on Evolutionary Game Theory，PCTBEGT）模型定义如下：

　　PCTBEGT={I，S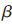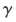，，，ESS，RD，U}

　　其中：

　　（1）I={1，2，…，n}表示无线网络中节点的集合，即博弈者的集合（n∈N+）；

　　（2）S={S*，M}表示博弈者所选择的策略集，S*表示纯策略组合，M表示混合策略组合；

　　（3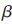）表示网络的吞吐量；

　　（4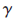）表示网络的定价函数；

　　（5）ESS表示演化稳定策略；

　　（6）RD表示复制者动态；

　　（7）U={u，f}表示博弈者的收益函数集。

　　1.2 节点的定价函数和收益函数

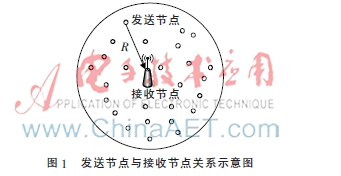
　　在无线网络中，发送节点与接收节点的关系如图1所示。假设在一定范围内移动节点i具有接收者R（i）的概率为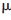，并定义一个随机变量R表示发送节点与接收节点之间的距离，设（r）是R的概率密度函数，则。假设接收节点的分布服从参数为v的泊松分布，则概率密度函数（r）可表示为。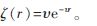

　　1.2.1 节点的定价函数

　　为了使网络性能得到优化，将节点的定价函数设为随发射功率的增加而增大的函数，其公式表示为[5]：

　　其中，gi表示发送节点i以功率pi发射时的链路增益。

　　1.2.2 节点的收益函数

　　节点的发射功率以及来自周围节点的干扰决定了该节点的收益，则发送节点i的收益函数f为：

　　其中，pi表示节点i的发射功率；表示收益参数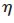；表示定价参数；C表示信道的极限信息传输速率，当用此速率进行传输时，可以做到不产生差错，具体公式为[6]：

　　C=Wlog2（1+P/N）（3）

　　其中，W表示信道的带宽（单位Hz），P表示信道内所传输信号的平均功率，N表示信道内部的高斯噪声功率。

　　1.3  PCTBEGT模型中演化稳定策略（Evolutionarily Stable Strategy，ESS）的唯一存在性

　　引理 对于节点密度在[0，R]上的密度函数?灼（r），函数h∶[0，1]是连续的并且严格单调的。其定义为：

　　现在证明混合策略（ESS，ESS）是一个均衡策略。为了证明这个结论，在所有m≠ESS的情况下（m表示博弈者中的突变者个体所选择的策略），比较式（8）和式（9）：

　　这样，可以用定价参数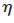作为工具生成一个用户的激励机制，从而调整它们的发射功率。当是递增的，演化稳定策略ESS也是递增的。这就意味着在增加定价函数的情况下，移动节点所对应的突变策略的侵略性在减小。

　　1.4 网络吞吐量

　　假定节点的总数为n，在最坏的情况下，每个节点都有n-1个干扰用户。由PCTBEGT模型可知，在无线网络的功率控制中，节点成功传输数据包的概率与节点数量和节点的收益有关。一个节点成功传输数据包的概率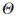为：

　　其中，表示在一定范围内移动节点i具有接收者R（i）的概率；n表示网络中的节点数目，即PCTBEGT模型中博弈者的个数。

2 仿真验证

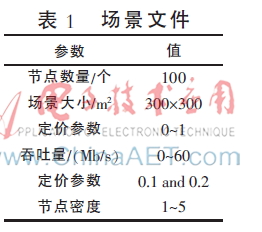
　　选取100个节点，节点间采用半双工通信且均共享信道，具体参数设置如表1所示。

　　2.1 定价参数对网络吞吐量的影响

　　假定根据参数为?自的泊松分布，接收节点随机分布在一个平面上，即?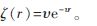。由式（3）和式（4）可知，节点在均衡点的功率水平可表示为：

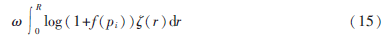
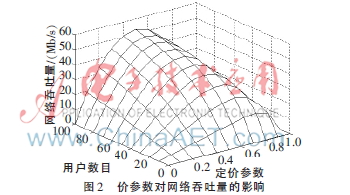
　　由式（14）和式（15）可得发送节点的分布密度和定价参数对网络吞吐量的影响如图2所示。从图中可以看出，定价参数是节点收益函数一个很重要的参数。随着定价参数?浊的增大，网络的吞吐量是逐渐增多的，当定价参数超过某一单位值后，吞吐量?茁逐渐减少。可见对于定价参数的选取并不是越大越好，而是有确定的界限和范围。

　　2.2 节点分布和定价参数对ESS的影响

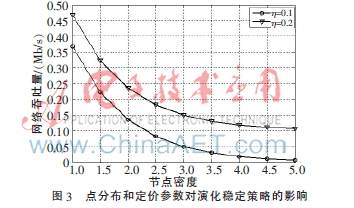
　　引入定价函数可以优化网络系统的性能和资源的利用率，其作为一种工具可用来生成节点的激励机制，进而调整节点的发射功率。节点的分布密度和定价参数对演化稳定策略的影响如图3所示。从图3可以看出，在同一节点密度的情况下，高定价策略占取优势；但随着节点密度的增加，演化稳定策略整体上是递减的，即节点变的越来越没有侵略性了，从而在一定程度上避免了博弈者中突变者个体的入侵和干扰。

3 结论

　　本文将演化博弈论引入到无线网络的功率控制中，建立PCTBEGT模型，在此模型的基础上证明演化稳定策略的唯一存在性并给出基于演化博弈论的吞吐量计算方法，最后用MATLAB进行实验仿真。结果表明，演化博弈论可以提高吞吐量，有效解决非合作系统行为，从而提高网络资源的利用率。

　　参考文献

　　[1] 李方敏，徐文君，刘新华.无线传感器网络功率控制技术[J].软件学报，2008，19（3）：716-732.

　　[2] Li Mingxin， Chen Shanzhi， Xie Dongliang， et al. Resource allocation and admission control based on non-cooperation game in heterogeneous wireless networks[J]. Journal of Software， 2010， 21（8）： 2037-2049（in Chinese）.

　　[3] ALTMAN E， BOULOGNE T， EL-AZOUZI R， et al. A survey on networking games in telecommunications[J]. Computers Operations Research， 2006， 33（2）： 286-311.

　　[4] SPYROPOULOS T， PSOUNIS K， RAGHAVENDRA C S. Efficient routing in intermittently connected mobile networks： the multiple-copy case [J]. ACM/IEEE Transaction on Networking， 2008， 16（1）：63-76.

　　[5] ALTMAN E， HAYEL Y. A Stochastic evolutionary game of energy management in a distributed aloha network[C]. Proc of the 27th Conference on Computer Communications（INFOCOM2008）， Piscataway， NJ： IEEE， 2008： 1759-1767.

　　[6] 谢希仁.计算机网络[M].北京：电子工业出版社，2007.