谢 瑜1，高晓智1，2

（1.上海海事大学 信息工程学院，上海 201306； 2.阿尔托大学 自动化与系统技术系，芬兰 赫尔辛基 FI-00076）

　　摘  要： 整数规划是NP困难（Non-deterministic Polynomial-time hard，NP-hard）的经典问题之一。整数规划的花授粉算法（Integer Flower Pollination Algorithm，IFPA）是采用截断取整的方法，将最近开发的花授粉算法（Flower Pollination Algorithm，FPA）扩展到求解整数规划问题。通过对测试函数集进行仿真实验，结果表明IFPA拥有很好的性能和很强的全局寻优能力，可以作为一种实用方法用于求解约束整数规划" title="无约束整数规划" target="_blank">无约束整数规划和有约束整数规划问题。

　　关键词： 无约束整数规划；约束整数规划；测试函数；花授粉算法；最优化

0 引言

　　整数规划问题是运筹学中的一个重要研究课题，它广泛存在于各个领域，如机械、化工、经济、生物、军事等。

　　对于变量维数较小的整数规划问题，传统的求解方法[1]有分支界定法、割平面法以及将两者结合起来的分支割平面算法、隐枚举法等；对于较大规模的问题，传统的计算方法比较耗时，通常先采用实数域的一些优化算法，再将计算结果进行取整后作为整数规划的近似解。但在实际应用中，取整运算常常导致约束的不满足或远离最优解。进化计算方法提出以后，已有许多学者应用遗传算法、蜂群算法[2]、粒子群算法[3-5]等求解整数规划问题。

　　花授粉算法[6]（Flower Pollination Algorithm，FPA）是剑桥大学的Yang Xinshe受启发于花授粉过程提出的一种具有全局收敛的新型搜索算法，该算法主要优点是参数少、操作简单、易实现、随机搜索路径和寻优能力强等。目前，对花授粉算法的研究还处于起步阶段，主要集中在连续函数的优化问题[6-7]。

　　本文的主要目的是拓展连续函数优化中的花授粉算法，从而开发出整数规划的花授粉算法（Integer Flower Pollination Algorithm，IFPA）。通过仿真实验验证了所提算法的有效性，结果表明该算法具有良好的全局寻优能力和良好的收敛速度。

1 基本花授粉算法

　　1.1 花授粉的特性

　　花授粉可以采取两种主要形式：非生物传粉和生物传粉。约90％的花卉属于生物授粉，约10％的授粉采取非生物形式，不需要任何传粉者。传粉者是非常多样的。据估计，至少有两百万种传粉者，它们也可以开发出所谓的花恒常。即这些传粉者往往只拜访某种特定的花卉品种，而绕过其他花种。

　　授粉可以通过自花授粉或异花授粉来实现。异花授粉意味着授粉可发生于不同植物的花粉，而自花授粉是一朵花的受精来自同一种植物的同一朵或不同朵花的花粉，如桃花。

　　异花生物授粉可能发生在长距离的情况，并且传粉者如蜜蜂、鸟类以及苍蝇能飞很长的距离，因此，它们可以被看作是全局授粉。此外，蜜蜂和鸟类可能表现为莱维飞行行为，其飞行步长服从莱维分布[8]。根据两朵花的相似性或差异性，花恒常可以被用做一个步长增量。

　　1.2 花授粉算法

　　花授粉算法是受启发于开花植物的花授粉过程，已经扩展到多目标的优化。为了模拟该过程，需要做以下假设：

　　（1）生物异花授粉被认为是全局授粉过程，且传粉者以莱维飞行的方式传粉。

　　（2）非生物自花授粉被认为是局部授粉。

　　（3）花恒常可以被认为是正比于某两朵相似性的繁殖概率。

　　（4）局部授粉和全局授粉由转移概率P∈[0，1]控制。由于物理的近似性和其他因素（例如风），局部授粉在整体授粉活动中有显著的偏重P。

　　基于以上假设，可以给出基本FPA的更新方程。在全局授粉中，花粉通过传粉者（例如昆虫）传播，并且花粉可移动很长的距离。因此，假设（1）和（3）可以用数学公式表示为：

　　其中，x是花粉i在迭代次数t下的位置矢量，g*是当前所有位置中的最优，γ是控制移动步长的比例因子。这里L（λ）是表示花粉强度的参数，使基于莱维飞行的步长大小更具体。因为昆虫可以以不同的距离步长移动很长的距离，因此莱维飞行可用于有效地模拟这种特性。L>0的莱维分布为：

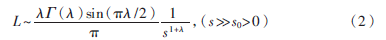
　　其中Γ（λ）是标准伽马函数，其分布对较大步长s>0是有效的。理论上须|s0|>>0，但是实际上s0可以小至0.1。产生步长最有效的方法是曼特尼亚算法，通过使用两个高斯分布的U和V变换计算步长大小s：

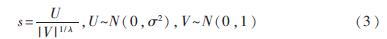
　　这里U~N（0，σ2）是指高斯正态分布具有零均值和σ2的方差。方差可由下式计算：

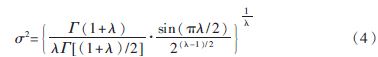
　　对于一个给定λ，σ2是一个常数。

　　在数学上已经证明了曼特尼亚算法可以产生服从莱维分布的伪随机样本。参考文献[7]中使用该伪随机数的算法绘制了一个连续50步大小的莱维飞行，如图1所示。

　　对于局部授粉，假设（2）和（3）均可表示为：

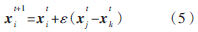
　　这里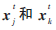表示同一品种不同花上的花粉。这实质上是模仿有限邻里的花恒常。在数学上，如果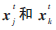是在同一品种或同一群体中选择出来的，并定义ε是在[0，1]上的均匀分布，则局部授粉即为局部的随机游走。

　　大多数花授粉活动都可以发生在局部和全局范围。在实践中，相邻或附近的花相比于距离较远的花更容易被局部授粉。大多数情况下，P=0.8时可取得较好结果。花授粉算法的基本步骤可以概括为伪代码如下：

　　目标函数f（x），x=（x1，…，xd）T

　　初始花粉种群xi（i=1，2，…，n）和vi（i=1，2，…，n）

　　寻找初始种群中的当前最优值g*

　　定义转移概率P∈[0，1]

　　While（t>误差容量）

　　for i=1：n（种群中所有的n个花粉）

　　if rand<p

　　取一个遵守莱维飞行的步长矢量L（d维）；

　　通过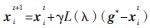更新所有花粉的位置；

　　边界约束检查；

　　else

　　取一个服从均匀分布的ε；

　　在所有解决方案（花粉）中随机选择j和k；

　　通过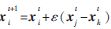更新局部花粉的位置；

　　边界约束检查；

　　end if

　　评价所有新的解；

　　如果新的解较好，接受新的解；

　　end for

　　end while

　　2 整数规划的花授粉算法

　　整数规划问题可描述为：

　　min/maxf（x），x∈S?哿Zd（6）

　　其中Zd为所有d维格子点组成的点集，S为问题的所有可行解集。在求解过程中，可采取两种截断取整的方法：一是在循环迭代的过程中，先将每个花粉的位置进行取整操作，然后计算其对应的函数值，此外的其他过程则完全与连续域函数优化的过程一致；二是保持连续域函数优化的过程，只在比较和评价目标函数值的过程中，对花粉位置取整并计算取整后的位置所对应的目标函数适应值。

　　经实验验证，第二种方法的效果明显优于第一种方法。所以，将第二种方法的思想应用到基本FPA中，可得本文提出的整数规划的花授粉算法。其主要步骤如下：

　　（1）参数和种群初始化。迭代次数t=0，给定种群数量n，局部授粉和全局授粉的转移概率P。然后随机产生一个种群，产生方式为：

　　x=low（j）+（ub（j）-lb（j））×rand（），i=1，2，…，n，j=1，2，…，d（7）

　　其中，“0”表示第0函数，d为待优化函数f（x）所含决策变量的个数，即维数。

　　（2）计算目标函数适应值。令X=round（x），分别计算x对应的目标函数适应值fit（i）=f（xi0）和Fit（i）=f（Xi0）。这里，xi0和Xi0均为d维行向量，fit和Fit均为n维行向量。分别找出fit和Fit中最好的元素（即最小的元素）及其对应的可行解，将fit和Fit中最好的元素分别记为fitbest和Fitbest，fitbest和Fitbest分别对应的可行解记为xbest和Xbest。

　　（3）判断是否满足算法结束条件，如果满足，即Fitbest等于全局最优值时，则转步骤（8），否则，转步骤（4）。

　　（4）利用转移概率P与一个随机产生的介于0和1之间的随机数比较结果，实现对种群位置的再次更新：当随机数大于P时利用式（1）对种群位置进行更新，否则利用式（2）更新。

　　（5）利用步骤（2）中方法，计算种群中每个花粉对应的目标函数适应值，即确定fitbest、Fitbest、xbest和Xbest。

　　（6）评价当前目标函数值Fitbest，并与历史最优函数值比较，确定当前迭代最优函数值。

　　（7）转步骤（3）。

　　（8）输出寻优得到的结果。

3 实例验证

　　以下实验过程的运行环境是Window7系统下的MATLAB2013a。选择参考文献[9]中的测试函数来验证所提出的IFPA在无约束整数规划问题中的应用；选择参考文献[5]中的实例来验证IFPA在约束整数规划问题中的应用。

　　3.1无约束整数规划测试函数

　　f1（x）=100（x2-x12）+（1-x1）2（8）

　　最优解为x*=（1，1），对应的最优值为f1（x*）=0。

　　f2（x）=（9x12+2x22-11）2+（3x12+4x22-7）2（9）

　　最优解为x*=（1，1），对应的最优值为f2（x*）=0。

　　f3（x）=（x1+10x2）2+5（x3-x4）2+（x2-2x3）4+10（x1-x4）4（10）

　　最优解为x*=（0，0，0，0），对应的最优值为f3（x*）=0。

　　f4（x）=-3 803.84-138.08x1-232.92x2+123.08x12+203.64x22+182.25x1x2（11）

　　最优解为x*=（0，1），对应的最优值为f4（x*）=-3 833.12。

　　f5（x）=‖x‖1=|x1|+|x2|+…+|xd|（12）

　　最优解为xi*=0，i=1，2，…，d，对应的最优值为f5（x*）=0。

　　f6（x）=xTx=x12+x22+…+xd2（13）

　　最优解为xi*=0，i=1，2，…，d，对应的最优值为f6（x*）=0。

　　f7（x）=2x12+3x22+4x1x2-6x1-3x2（14）

　　最优解为xi*=0，i=1，2，…，d，对应的最优值为f9（x*）=0。

　　f10（x）=100（x2-x12）2+90（x4-x32）2+（1-x3）2+10.1（x2-1）2+19.8（x2-1）（x4-1）（17）

　　最优解为x*=（1，1，1，1，1），对应的最优值为f10（x*）=0。

　　f11（x）=（1.5-x1（1-x2））2+（2.25-x1（1-x22））2+（2.625- x1（1-x23））2（18）

　　最优解为x*=（2，0），对应的最优值为f11（x*）=0.703 13。

　　f12（x）=（x12+x2-11）2+（x22+x1-7）2（19）

　　最优解为x*=（3，2），对应的最优值为f12（x*）=0。

　　在给定误差容量为10-5时，用整数花授粉算法来找到以上实例中各函数的最优解。IFPA中种群规模n取为40，其转移概率P取0.8，该算法独立运行20次。

　　实验统计指标有7个，前三个是20次独立运行所得目标函数值的最好值、平均值及最差值；第四到第六个包括这20次成功寻优中使用的最小迭代次数、平均迭代次数、最大迭代次数；最后一个指标是20次独立循环消耗的总时间（单位：s）。花授粉算法的运行结果见表1。

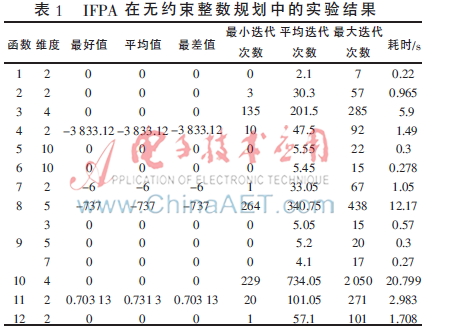
　　由表1可以看出，IFPA具有较强的全局搜索能力，能够在更短的时间范围内收敛到全局最优值，即IFPA可以很好地解决无约束整数规划问题。

　　3.2 有约束整数规划

　　花授粉算法不仅可以解决无约束整数规划问题，同样可以解决有约束的整数规划问题。

　　实例1：

　　maxf（x）=3x1+2x2

　　s.t.2x1+3x2≤2 0054x1+x2≤3 001x1，x2≥0，x1，x2∈Z

　　理论上，该线性整数规划的最优解为（700，201），最优值为2 502。若去掉整数的约束，则线性规划的最优解为（699.8，201.8）。利用IFPA可以很容易找到与理论相同的解x*=（700，201），f（x*）=2 502。程序仿真时，每次迭代的最优值随迭代次数的函数关系如图2所示。

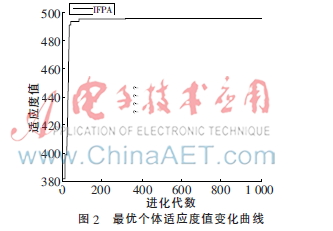
　　从图2可见，前270代当前最优值呈上升趋势，花授粉算法对有约束非线性整数规划的求解有很快的收敛速度。

　　实例2：

　　maxf（x）=x12+x22+3x32+4x42+2x52-8x1-2x2-3x3-x4-2x5

　　s.t.x1+x2+x3+x4+x5≤400x1+2x2+2x3+x4+6x5≤8002x1+x2+6x3≤200x3+x4+5x5≤2000≤xi≤99（i=1，…，5）

　　理论上，该非线性整数规划的最优解为（50，99，0，99，20），最优值为51 568。利用IFPA很容易找到与理论相同的解x*=（50，99，0，99，20），f（x*）=51 568。该实例仿真函数关系如图3所示。

　　从图3中前140代当前最优值的上升趋势来看，可行域内的整数规划花授粉算法对有约束非线性整数规划的求解也有很快的收敛速度。

4 结论

　　在工程和工业中解决整数规划问题往往是具有挑战性的，因此需要特殊的技术来解决。近年来，启发式方法已经显示出其前景并得到了普及。本文提出了一种整数规划的花授粉算法（IFPA），将最近提出的花授粉算法拓展到解决整数规划的问题中。经过标准测试函数和实例的验证，说明了该算法能够很好地解决有约束整数规划和无约束整数规划问题。

参考文献

　　[1] 杜枯康，英凯.整数规划问题智能求解算法综述[J].计算机应用研究，2010，27（2）：408-412.

　　[2] LIU Y， MA L． Bee colony foraging algorithm for integer programming[C]. Business Management and Electronic Information（BMEI）， 2011 International Conference on． IEEE，2011，5： 199-201．

　　[3] 谭瑛，高慧敏，曾建潮．求解整数规划问题的微粒群算法[J]．系统工程理论与实践，2004，24（5）：126-129．

　　[4] 高尚，杨静宇．非线性整数规划的粒子群优化算法[J].计算机应用，2007，28（2）：126-130．

　　[5] 祁辉，熊鹰，周树民.基于粒子群算法的整数规划问题的求解算法[J].江汉大学学报，2009，37（1）：25-29．

　　[6] YANG X S. Flower pollination algorithm for global optimization[J]. In Unconventional Computation and Natural Computation， 2012，7445：240-249.

　　[7] YANG X S， KARAMANOGLU M， HE X S. Multi-objective flower algorithm for optimization[J]. Procedia Computer Science，2013（18）：861-868.

　　[8] YANG X S. Review of Meta-heuristics and generalised evolutionary walk algorithm[J]. International Journal of Bio-Inspired Computation，2011，3 （2）：77-84.

　　[9] 吴炅，健勇.整数规划的布谷鸟算法[J].学理论与应用，2013，33（3）：99-106.