姜慧鹏，刘宜成，蒲明，庞冰洋

　　（四川大学 电气信息学院，四川 成都 610065）

       摘要：为了改善单相LCL型并网逆变器的稳态性能和瞬时响应性能，提出了一种基于改进切换函数的滑模控制策略。该控制策略从开关函数模型角度分析单相LCL型并网逆变器的数学模型，得到系统的状态方程。通过选取合适的滑模面，求得等效控制。提出一种改进的切换函数设计滑模控制器，并用李雅普洛夫第二法证明了系统的稳定性。最后用MATLAB对系统进行了仿真实验，仿真结果表明，采用该控制策略的逆变器具有较好的稳态性能和瞬时响应性能，其并网电流畸变率为0.41%。

　　关键词：滑模控制；并网逆变器；LCL；李雅普洛夫第二法

0引言

　　目前，煤炭、天然气等不可再生资源的日益消耗，使环境污染越来越严重，各国都在积极寻求高效、清洁的可再生能源，利用太阳能发电的技术及设备成为研究热点［1］。

　　并网逆变器就是其中的一项关键设备，它将光伏电池输出的直流电转换为有谐波的交流电。为了减小谐波的影响，需要对逆变过后的并网电流进行滤波［2］。LCL滤波器的体积小且能有效滤除电流中的高频分量，因此被越来越多地采用。不过这种滤波器的电容支路会引起谐振，这就要求控制器具有更强的稳态性能和更好的响应性能［35］。

　　逆变器控制方法已有很多学者研究，常见的几种也各有其优劣势。滞环控制稳定性好、响应快，但要求开关频率高，损耗加大［68］。PI控制技术成熟、可靠性高，但具有稳态误差［910］。另外有学者采用具有较好稳定性、鲁棒性和瞬时响应特性的滑模控制［1011］，但对逆变器的模型做了一定的简化，且在控制器中引入了基于传递函数模型的PI控制。本文从开关函数角度出发，推导了单相LCL型并网逆变器的数学模型，并采用基于改进切换函数的滑模控制策略设计控制器。最后，用MATLAB仿真验证了控制器的有效性和正确性。

1电路结构及数学模型

　　单相LCL型并网逆变器采用桥式逆变，并网侧用LCL滤波器滤波，电路结构如图1 所示。其中，Udc、Uin、UC和e分别直流侧电压、逆变器输出电压、滤波电容电压和并网电压；iL、iC、ig分别为流过逆变器侧电感L1的电流、流过滤波电容Cf的电流和流过网侧电感Lg的并网电流［12］。　

　　由基尔霍夫电压和电流定律，列出各个回路的电路方程如下：

　　其中，Sk为开关函数。

　　以上方程可化简为：

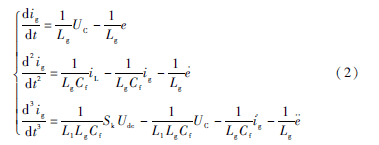
　　取x=［x1x2x3］=［ig-irefg-refg-ref］,u=Sk，则有状态方程：

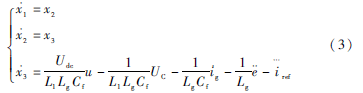
　　2滑模控制器的设计

　　滑模控制有基于等效控制和基于趋近律的两种实现方法［13］，这里采用基于等效控制的方法。设计步骤如下。

　　首先选取滑模面：

　　s=x1+k1x2+k2x3（4）

　　其中，k1、k2为大于零的常数。

　　由s=0得：

　　=1+k12+k23=0 （5）

　　将式（3）代入推导得：

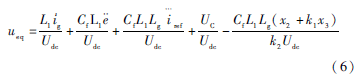
　　在取切换控制时，采用改进的切换控制函数：

　　un=－k3s－k4sgn(s)（7）

　　其中，k3、k4为大于零的常数。则可以得到控制量u=ueq+un，即：

　　这里得到的控制量是一个连续的时间信号，需要通过一个PWM产生器，产生4个开关信号来控制全桥的对应开关。

　　3稳定性的证明

　　取正定标量函数：

　　根据李雅普诺夫第二法的相关论述可知系统稳定。

4系统仿真分析

　　为了证明改进的滑模控制器的有效性，用MATLAB对一台额定容量为1 kVA的并网逆变器进行了仿真，控制器分别采用双闭环（PI+P）控制策略［14］和改进的滑模控制策略。表1列出了系统的仿真参数。

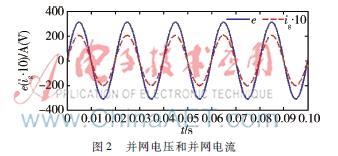
　　为观察系统的稳态性能，在并网逆变器稳定运行时，分析并网电压与并网电流，并对并网电流做FFT分析。为了突出对比，将电流放大了10倍显示。

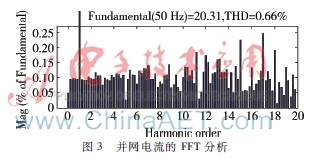
　　采用双闭环（PI+P）控制策略时，并网电压和并网电流如图2所示，并网电流的FFT分析如图3所示，并网电压与并网电流同频同相，THD为0.66%。

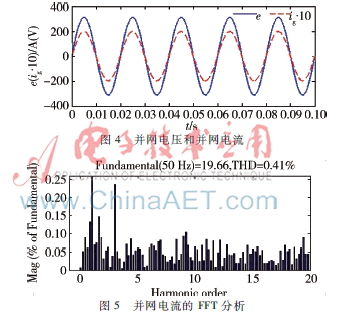
　　采用改进的滑模控制策略时，并网电压和并网电流如图4所示，并网电流的FFT分析如图5所示，并网电压与并网电流同频同相，THD为0.41%，系统具有较好的稳态性能。

　　为观察系统的瞬时响应性能，分析了负载在满载与半载之间跳变的情况，得到了跳变（跳变时刻t=0.025 s）时的并网电流波形。

　　采用双闭环（PI+P）控制策略时，半载至满载跳变的情况如图6所示，满载跳变至半载的情况如图7所示，并网电流能在0.002 s（0.1个周期）内恢复稳定运行，且有最大为0.7的超调。

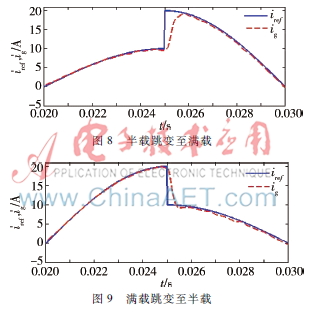
　　采用改进的滑模控制策略时，半载至满载跳变的情况如图8所示，满载跳变至半载的情况如图9所示，并网电流能在0.001 s（0.05个周期）内恢复稳定运行，且没有超调，系统具有较好的瞬时响应性能。

5结论

　　本文推导了单相LCL型并网逆变器的数学模型，提出了一种基于改进切换函数的滑模控制策略。1 kVA并网逆变器的仿真研究表明，采用本文所提出的滑模控制策略，系统具有较好的稳态性能，在负载跳变后，系统能快速地恢复稳定运行，具有很好的瞬时响应特性。

参考文献

　　［1］ 艾欣,韩晓男,孙英云.大型光伏电站并网特性及其低碳运行与控制技术［J］.电网技术,2013,37(1):1523.

　　［2］ 李泽斌,罗安,田园，等.LCL型光伏并网逆变器电流内环控制方法［J］.电网技术,2014,38(10):27722778.

　　［3］ 赵晋斌,张元吉,屈克庆，等.单相LCL并网逆变器控制策略综述［J］.电工技术学报,2013,28(10):134142.

　　［4］ 戴训江,晁勤.基于LCL滤波的光伏并网逆变器电流滞环控制［J］.电力电子技术,2009,43(7):3335.

　　［5］ 臧鹏，洪峰，辛张楠，等.LCL滤波器型双Buck并网逆变器［J］.电子技术应用,2015,41(10):129132.

　　［6］ 马小虎,袁晓玲,施俊华.改进滞环电流控制策略在光伏并网中的研究［J］.电源技术,2013,37(11):20192022.

　　［7］ 彭传彪,王少坤,王晓锋，等.自适应滞环电流控制逆变器复合控制策略［J］.电力自动化设备,2011, 31(7):4247.

　　［8］ 黄少辉，林培杰，程树英，等.电流型并网逆变器的模糊滞环控制［J］.微型机与应用,2015,34(13):7376.

　　［9］ 韩金刚,朱瑞林,汤天浩，等．LCL型并网逆变器并网电流复合控制研究［J］.太阳能学报,2014,35(9):15991605.

　　［10］ 何翔,张代润.基于滑模控制的三相光伏并网逆变器研究［J］.电源技术,2014, 38(4): 672675.

　　［11］ 王朗珠,丁茂桃,郑连清.一种新的三相电压型PWM整流器控制［J］.电力电子技术,2012,46(5):5759.

　　［12］ 黄挚雄,徐保友,沈玲菲，等.LCL并网逆变器新型电流双闭环控制策略研究［J］.电力系统保护与控制,2012,40(17):15.