0 引言

    在人工智能领域，机器学习和自适应等算法是主要研究方向，而面对智能家居领域的控制，机器学习等方法并不合适。原因如下：首先，样本空间不足，没有足够的训练数据^[1]。例如，一般城市家庭的生活作息是以星期为单位，即使只收集一个家庭50组数据就需要花费一年的时间，这在实际运用中行不通；其次，学习难度大。准确性地学习一个人或一个家庭的生活作息难度非常大，因为人不存在绝对的内在作息规律，随机性非常大^[2]；最后，计算能力不足。人工智能一般需要很大的计算量，而智能家居的控制算法基本运行在单片机或微控制器上，这些处理器相对PC或服务器级别的处理器而言，主频低，单核，位长短和浮点计算能力欠缺或不足^[3-4]。

    基于以上事实，智能家居控制算法不能采用既有模型和思路来实现。算法必须具备不需要学习样本、应对变化反应速度快、计算量小和容易被编码等特点^[5-6]。智能家居的控制算法是一个具体场景的应用，故在学术上对此的研究并不多。本文通过不断的尝试和实验，提出了以真假值为主要计算手段的TF算法。 

1 算法概述

    为简化算法的表达并增强实用性，引用电热水器作为家庭设备终端进行说明，该设备是中国普通家庭普及率最高的家用电器。一般家庭使用热水的习惯集中在早晨和晚上，而电热水器却是全天24小时保存热水，造成了电能浪费[7]。以中国南方为例，夏季即使白天和夜里不使用热水，热水器一般会空烧一次，而在冬天则空烧的频率更大，严重造成了电能浪费。由于家庭组成千变万化，不可能通过提前在热水器中预置一个全能的控制算法来做实际控制，但可以在热水器中预置一个具备最低级控制能力并同时具有收集分析历史数据和根据数据的变化动态做出决策的TF算法。在实际使用中，通过它在不同的家庭环境中控制热水器的同时提取用户数据，制定出与特定使用者相匹配的控制策略。

2 建立表达模型

    热水器的使用是现实世界中的具体问题，如果要想通过算法或程序来进行智能控制和管理，则首先需要建立相关的数据表达模型，这个表达模型应该容易被计算机表示和处理，只有在这个表达模型基础上，才能进行进一步计算等处理。

2.1 原始数据采集

    算法控制的直接对象是热水器，因此要了解对应家庭使用热水的时间段数据，而数据只有通过热水器获知。热水在实际使用中总是时断时续，通过统计发现，一个人的简单洗漱过程一般会持续10~15分钟，平均开关水龙头3次^[8]，而如果把这些琐碎的时间片全部收集起来进行处理则没有任何意义。数据收集采取的办法是两次使用热水的时间差在半个小时以内，则算为一次。通过使用该收集数据的方法抽查并记录某一家庭某一周使用热水的数据如下所示：

    周一： 06:28-07:03\11:40-13:59\18:32-00:05

    周二： 06:53-07:28\19:20-22:22

    周三： 06:10-07:40\19:43-00:20\22:21-00:12

    周四： 06:31-06:58\17:46-20:19

    周五： 06:11-07:42\17:17-00:28

    周六： 09:01-11:11\12:40-14:22\08:03-01:16

    周日： 08:40-10:15\11:49-15:48\18:53-23:20

2.2 数据处理和离散化

    为了更加清晰地发现规律，需要对原始采集的数据做进一步处理，实质是将其工作区间扩大和计数单位离散化。具体的处理方法是将起始时间在xx:01-xx:30和xx:31-xx:60(xx:00)之间的数据划归到xx:00和xx:30。结束时间在xx:01-xx:30和xx:31-xx:60(xx:00)之间的数据划归到xx:30和xx+1:00。处理过的数据如下所示：

    周一： 06:00-07:30\11:30-14:00\18:30-00:30

    周二： 06:30-07:30\19:00-22:30

    周三： 06:00-08:00\19:30-21:30\22:00-00:30

    周四： 06:30-07:00\17:30-20:30

    周五： 06:00-08:00\17:00-00:30

    周六： 09:00-11:30\12:30-14:30\08:00-01:30

    周日： 08:30-10:30\11:30-16:00\18:30-23:30

    通过将处理过的数据与原始数据对比可以发现，原始数据是被处理过数据的一个真子集。虽然原始数据经处理后发生变化，但可以在不影响使用者数据提取的前提下简化计算工作，所以进行这样的数据处理是必要的。

    为了更清晰地看清规律将数据可视化，根据处理后的数据得出表1的位图表。纵向为时间单位，每半个小时为一个计算单位；横向为7个时间单位，每天是一个计算单位。

    根据实际使用情况每半个小时对应着布尔值“真”或是“假”，用T表示“真”，F表示“假”。通过表1发现，只要控制算法最终能确定每个格子的值取真还是假即可。至此，将实际问题中的模拟量转化成了由位图表示的计算机可处理的表达模型，整个算法也是基于位图展开的。

2.3 应用场景分析及研究重点

    算法的最终使用场景是在没有任何历史数据存在的情况下，收集数据与分析数据同步进行。由于使用家庭不同和节气等原因，生活作息会不断变化，即使是通过累积历史数据分析并得到了决策方法，也不能以后就一直使用这个方法，还必须持续地分析过去的数据，形成与使用者家庭当前最匹配的控制方法。

    在现实中，城市居民的生活往往以周或天为一个规律性的周期，所以需要加入一个控制周期参数LP(learning period)来定义控制周期。根据实际情况给LP取两个值，如果是天，用LP=d(day)表示；或者是星期，用LP=w(week)表示。

    在LP=d的情况下，前一天的数据会一定程度地影响第二天对热水器的控制，这种情况适用于不是以星期为生活周期的家庭。

    在LP=w的情况下，前一个星期的输入数据会在一定程度上影响下个星期对控制器的控制。其实LP=w是由LP=d的组合而行成的情况，以每周的星期三为例，当前星期的周三只能借鉴前一个星期周三的历史数据，本质还是LP=d的情况，所以本论文重点研究LP=d的情况。

3 算法原理

    当前控制位图(A)+最近一天的数据位图(B)=最终控制位图(C)(计算方法)，如图1所示。

    其中当前控制位图(A)表示当前的控制决策；最近一天的数据位图(B)表示最新的历史数据，它是算法的输入；最终控制位图(C)表示通过计算得出的最新控制决策结果，它是算法的输出。而在整个算法工作流程中，计算方法是核心，直接决定着最终控制结果的好坏。

3.1 TF初步方法

    最简单的初步计算方法是采取类似真值计算法来得出目标控制位图。以图1的07:00-07:30这一格为例来说明。图2给出了计算法则。

    这种策略完全参考最新一天的数据，把最近一天的数据当作下一天的控制方法。这种方法虽然简单，但是不具备灵活性和健壮性。尤其是对突然不规律的一天数据这种情况，完全没有抵御能力。另外也没有考虑到06:30-07:00和07:30-08:00等目标格附近对最终结果的影响，因为正常的生活作息都是在一定的区间内摇摆，必须要注重时间前后性的联系。

3.2 TF改进方法

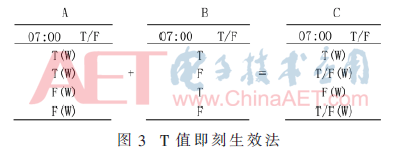
    初步方法除了参照最近一天的数据B外，并没有参考以前的数据，需要在初步方法基础上做进一步改进。要想参考以前的历史数据，需要把历史数据一定程度反映到当前控制位图A中。每一个格子在可以取真假值之外，需要再携带一个权值，这里用W表示。以W作为参考，面对最新一天的数据位图时，可以综合W的值来做出决策，而不是完全按照最新一天的位图信息来决定下一天的控制位图。初步方法有一点需要保留——T值即刻生效法，无论当前控制位图A的某一格子是T还是F，或者W取值是什么，只要最近一天数据位图B的对应格子是T，则下一天的控制位图对应格子做出的决策是T。采取“T值即刻生效法”是为了尽量不要遗漏工作时间，快速对变化做出反应，从而减少给正常生活带来麻烦。这也是整个算法的原则之一，实现手段是尽量使算法的T值域大于等于真正的T值域，这样可以更好地为智能生活带来方便。图3给出了“T值即刻生效法”的运算法则。

    W的一种取法是统计式的方式，即以T或F的总数为分子，T和F的和总数为分母。W的另外一种取法是记录式的方式，记录预定义的一段时间内连续的T或是F的总数。由于人的活动具有时间局部性，相同活动规律具有聚集性，第二种方法可以反映相应的聚集性和连续性，所以W采取第二种方式取值，具体的取法如下。

    用3个域来保存最近三天的T/F值记录。W的3个域初始值均为T，在未接触到使用者数据时，默认全天工作。W的动态变化如图4所示。

    W从整体上看是一个按着时间的先后顺序向左移动的记录。W保存的是使用者家庭最近过去三天的T/F值情况。

    在T值即刻生效法和W的约束下，需要新的计算法则，以W在n(n>=3)天后的情况为例来说明，如图5所示。

    以第n天的数据划分为两种情况。

    第一种情况：第n天的数据值为T。根据T值即刻生效法会直接得出控制结果为T。这种情况下不需要参考W的值。

    第二种情况：第n天的数据值为F。这种情况，T值即刻生效法不起作用，做决策的依据是查看第n-2天的数据值和第n-1天的数据值的真假。如果全部是F，则得出控制值为F；如果只有T存在，则会得出控制结果为T。该情况采取这种策略的目的是为由T向F变化提供一个容量为3的缓冲，只有连续三天为F才能确定为F，这些做法很好地体现了T值域最大可能性的覆盖真实情况。具体的计算法则如图6所示。

3.3 TF最终方法

    改进方法可以反映人们生活习惯的时间局部性，但其缺点是边界过于硬朗和容易造成控制漏洞。下面以图1的15:00一格为研究对象来说明。

    使用改进方法则只参考时间段15:00～15:30的当前控制位图A和15:00～15:30的最新历史数据B，然后得到15:00～15:30的控制结果C。而实际上，人们的生活行为是线性的，具有时间前后连续性。为此，除了需要参考15:00～15:30的当前位图和最近一天15:00～15:30的数据位图外，需要把它前一格的数据和后一格的数据作为参考，进行评估。截取图1的数据如图7所示。

    使用改进方法可以分别得到C的14:30格子、15:00格子和15:30格子的控制结果。为了反映时间的连续性，在C的基础上建立3个格子的关联。具体分为两种情况：

    第一种情况：当使用改进方法计算出15:00格子的控制结果为T，则依然遵守T值即刻生效法，不做任何操作，直接确定其最终控制结果为T。

    第二种情况：当使用改进方法计算出15:00格子的控制结果为F，并通过改进方法计算出14:30格子和15:30格子的控制结果。如果想要确定15:00格子的最终控制结果，需要参考其相邻格子的值。具体的办法是采取简单投票法，如果其他两个格子都是T，则15:00格子的最终控制结果为T；否则，15:00格子的最终控制结果为F。这种做法进一步加大了T域覆盖真实T的可能性。

    最终方法在初步方法和改进方法的基础上进行了改进和完善，去掉了初步方法和改进方法的缺点和不足，继承了它们的优点。最终方法具有对T变化反应迅速、对F变化反应迟缓，并具有柔和边界和防止控制漏洞等特性。

4 测试结果和评价

    对算法进行测试有模拟和实践两种方法。对于TF算法而言，由于没有方法对人的这种随机性行为进行模拟，所以采用模拟方法并不可行。故采用实践测试方法对TF算法进行测试。

    由于时间等因素的限制，对TF算法进行了小范围测试，统计以天为生活周期某一家庭使用热水器的数据，持续时间为10天。另外，为了说明算法的使用效果，把算法的控制结果和这一个家庭的数据进行对比，结果如图8所示。

    通过测试结果表发现，前三天是导入期，故TF算法具有最大工作时间，其控制的热水器是全天24小时工作，没有收敛，从第四天开始收敛。其中有两个参数需要统计，一个是命中率为93.9%，这个参数直接影响到使用者的体验，命中率越高，则用户越满意。非命中的格子在测试结果图8中已经被标记出来，非命中率为6.1%。

    从节能省电的角度来评价算法，则需要统计无效控制，去掉前三天的情况，无效控制率为36.7%。单纯从节能省电的角度来评价算法，这个参数越低，则电能利用率越高。但是，只有在命中率满足一定要求下，提升这个指标才有意义。

    由于学术界对智能家居智能算法的研究很少，故没有办法通过对比数据来证明算法性能，但可通过统计并对比使用TF控制算法前后的用电量来测试。表2分别统计了TF控制算法运行不同时间与平时的用电量比率。

5 结论

    本文从智能家居的智能控制的实际问题出发，分析了智能家居对智能算法的要求，建立了智能表达模型。通过实际测试TF算法，验证了该控制算法具有很好的智能性和健壮性，并具备很强的节能省电功能，可以满足智能控制的要求并被实践推广。

参考文献

[1] HU Q，LI F.Hardware design of smart home energy management system with dynamic price response[J].Smart Grid IEEE Transactions on，2013，4(4)：1878-1887.

[2] PANNA R，THESRUMLUK R，CHANTRAPORNCHAI C.Development of energy saving smart home prototype[J].International Journal of Smart Home，2013，7(1)：1-6.

[3] 马宪民，杨君锐.人工智能的原理与方法[M].西安：西北工业大学出版社，2002：9-28.

[4] MITCHELL T M.机器学习[M].北京：机械学习出版社，2008：1-20.

[5] ROBLES R J，KIM T H.Applications systems and methods in smart home technology：a review[J].International Journal of Advance Science and Technology，2010，15(3)：37-47.

[6] HAN D M，LIM J H.Design and implementation of smart home energy management systems based on zigbee[J].IEEE Transactions on Consumer Electronics，2010，56(3)：1417-1425.

[7] ZHOU X，ZHANG C S，ZHANG X W，et al.nRF905-based smart home system design[J].Shanxi Electronic Technology，2012，3(4)：38-42.

[8] LIAO G H，ZHU J B.Smart home system network architecture and implementation[M].Springer Berlin Heidelberg，Information and Management Engineering，2011：498-503.