王建宇1，刘宝柱1，蒲天骄2，于  汀2，唐茹彬1

　　（1.华北电力大学 电气与电子工程学院，北京 102206；2.中国电力科学研究院，北京 100192）

　　摘  要： 将发电机有功出力和无功出力同时作为控制变量，进行有功/无功协调优化。在优化过程中，考虑发电机安全运行极限，不断根据发电机当前有功出力值和机端电压值对无功出力约束限值进行更新，以保证发电机始终运行在其安全运行区域内。建立了计及发电机安全运行极限的电力系统有功/无功协调优化模型，并利用基于函数变换与广义逆的优化算法对其进行求解。借助函数变换可以很方便的处理不等式约束，由此导致变量增加而得到的不定方程组，又可利用广义逆的方法很好的予以解决。最后结合改进IEEE57节点系统作为算例，验证了本文所提优化方法的有效性和可行性。

　　关键词： 有功/无功协调优化；发电机安全运行极限；无功出力约束限值更新

0 引言

　　电力系统有功优化可以降低发电成本，无功优化可以降低网络损耗，二者在电力系统运行经济性中具有重要意义[1-2]。通常先通过有功优化制定有功发电计划，确定机组有功出力；然后在此基础上进行无功优化，通过调整各发电机节点无功出力来实现网损最低等目标。在此过程中平衡节点有功出力会进行相应调整，以平衡全系统网损，但其他发电机节点有功出力只能进行微调，甚至保持不变。文献[3]已指出将有功优化与无功优化分开进行的不合理性，此外还应考虑到如下几点：

　　（1）对于规模较大、发电机节点数较多的系统，进行无功优化时，如果仅靠平衡节点来调整系统有功平衡，可能会引起线路输送功率的上升，导致网损增加，其后果会与发电机无功出力调整带来的网损降低相互抵制，降低优化效益。

　　（2）若近负荷点的发电机节点有良好的经济性能，则定性分析可知，适当增加其有功出力则意味着经济性较差的机组出力降低，同时这还可以减少线路功率流动，从而降低网损。二者综合作用会使发电费用进一步降低。

　　为使电力系统运行更经济安全，本文不再分别进行有功优化和无功优化，而是将发电机有功出力和无功出力同时作为控制变量，进行有功/无功协调优化，同时在优化过程中计及发电机安全运行极限。该研究难点主要体现在不等式约束处理的两个方面：一是优化模型中需同时计入发电机有功/无功出力约束，导致不等式约束增加；二是发电机无功出力不仅有其自身约束的限制，而且其约束限值并非定值。

　　鉴于上述难点，本文选取基于函数变换与广义逆的优化算法[4]。在优化过程中，同时考虑发电机有功/无功出力约束，采取一定的更新策略，不断根据发电机当前有功出力值和机端电压值对其无功出力约束限值进行更新，以保证发电机始终运行在安全区域内。运用函数变换法对不等式约束进行处理，并运用牛顿－拉夫逊法结合广义逆求解非线性不定方程组，通过采取一定收缩策略，实现目标最优。

1 发电机安全运行极限分析

　　发电机安全运行极限图如图1所示，其安全运行会受到励磁绕组温升、定子绕组温升、原动机出力和静态稳定极限等约束的限制[5-8]，这一系列约束确定的区域即为发电机的安全运行区域[9]。

　　发电机运行在安全区域内需满足如下条件：

　　（1）发电机有功出力满足原动机出力约束，以及锅炉和汽轮机的技术最小负荷约束：

　　式中，Eqmax为发电机励磁电动势最大值；VG为发电机机端电压；XS为隐极发电机同步电抗；Iamax为发电机定子电流的最大值；δmax为最大功角。

2 有功/无功协调优化模型

　　2.1 目标函数

　　有功优化通常以发电成本最低为目标，无功优化通常以有功网损最低为目标，分别如下两式所示：

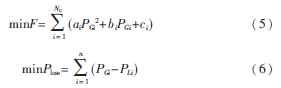
　　式中：F为发电成本；Ploss为系统有功网损值；PGi为节点i的发电机有功出力；PLi为节点i的负荷有功功率；NG为发电机节点总数；n为系统节点总数；ai、bi、ci为发电机节点的经济参数。

　　在电力系统有功/无功协调优化中，需将上述两目标综合考虑。文献[3]分析指出，以系统总发电成本最低为目标的优化结果，与分别优化负荷有功发电成本和系统有功网损发电成本的优化结果一致。因而可将式(1)作为电力系统有功/无功协调优化的目标函数。

　　2.2 等式约束

　　等式约束即潮流等式方程：

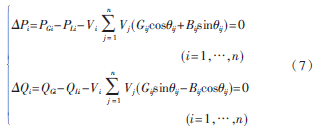
　　式中：QGi为节点i的发电机无功出力；QLi为节点i的负荷无功功率；Vi和Vj分别为节点i和j的电压幅值；ij为节点i和j的电压相角差；Gij和Bij分别为节点导纳矩阵的实部和虚部。

　　注意式(3)包括平衡节点对应的方程，这区别于常规潮流计算。因为对平衡节点，本文也考虑了有功/无功出力约束的限制，为保证在优化过程中平衡节点发电机出力不越限，需计及其相关约束。

　　2.3 不等式约束

　　不等式约束包括：

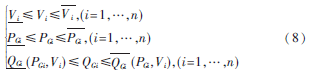
　　式中：表示节点i发电机有功出力约束的上下限值；   表示节点i电压约束的上下限值；(PGi,Vi)、(PGi,Vi)表示节点i发电机无功出力约束的上下限值，该值为发电机有功出力值和机端电压值的函数。对于有功出力或无功出力恒为零的节点，可将其出力上下限值均设为0。

　　本文旨在对电力系统有功/无功协调优化与传统的先有功优化后无功优化的方式进行对比分析，所以暂简化处理，不考虑其他控制变量。

3 无功约束限值更新策略

　　由式(2)～式(4)可见，无功出力约束限值是PGi和Vi的函数。在优化过程中，随着PGi和Vi的调整，无功限值应予以更新。

　　限于篇幅，基于函数变换与广义逆的优化算法原理见文献[4]。该算法在优化开始前首先进行一次约束潮流计算，并根据机组有功出力计算发电成本，以得到的变量解和发电成本作为随后优化过程的变量初始解和发电成本初值。之后的优化过程包括内外两层嵌套的循环，外层循环对发电成本逐步收缩，以降低费用，实现优化；内层循环为在当前发电成本下进行约束潮流计算的过程。

　　本文采取如下策略更新优化过程中的发电机无功出力约束限值：在每次由外层循环进入内层循环后，前几次迭代都不考虑更新，待迭代几次后，各变量的变化趋缓，此后每进行一次内层迭代都会基于当前发电机有功出力值和机端电压值，根据式(2)和式(3)的较小者更新无功出力约束上限值，根据式(4)更新无功出力约束下限值。

　　选取该策略可以在一定程度上解决以下问题：

　　（1）若每进行一次外层循环，才更新一次无功出力约束限值，则优化前进行的约束潮流计算中并未进行更新，这可能会使优化过程的变量初始解和发电成本初值不合理；而且在这种情况下，每两次更新间隔时间过长，这可能导致某一次外层循环结束时的更新结果在下次外层循环对应的内层循环中迭代几次后已不适用，计算精度降低。

　　（2）若内层循环每迭代一次，发电机无功出力约束限值更新一次，则更新过于频繁，可能会导致算法收敛性变差，运算时间过长；而且在内层循环刚开始的几次迭代计算中，各变量变化较剧烈，与最终收敛解相距甚远，此时即考虑无功出力约束限值更新意义不大。

4 算法流程

　　采用基于函数变换与广义逆的优化算法，考虑发电机安全运行极限，在每一次由外层循环进入内层循环后，从第3次迭代开始考虑发电机无功出力约束限值更新，在内层循环中当迭代超过30次时，即认为在当前收缩因子值下约束潮流不收敛，需减小收缩因子后再开始新一轮的优化，直至收缩因子达到其收敛阈值，优化过程结束。

　　算法步骤如下：

　　（1）变量赋初值，迭代次数N=0。

　　（2）判断优化是否开始，若开始，则继续；否则，转步骤（5）。

　　（3）判断收缩因子是否大于收敛阈值，若大于，则保存各变量当前值，迭代次数N=0，继续；否则，转步骤（11）。

　　（4）若连续收敛次数达到5次，则先增大收缩因子，再收缩发电成本；否则直接对发电成本进行收缩。

　　（5）计算功率不平衡量，判断最大功率不平衡量是否大于收敛精度，若大于，则继续；否则，转步骤（3）。

　　（6）迭代次数N=N+1，若N＞30，则转步骤（9）；否则，继续。

　　（7）生成扩展雅可比矩阵，求解修正量，对各变量进行修正。

　　（8）若N＞2，则基于发电机有功出力值和机端电压值，根据式(2)和式(3)较小者更新发电机无功出力约束上限值，根据式(4)更新发电机无功出力约束下限值，转步骤（5）；否则，直接转步骤（5）。

　　（9）判断优化是否开始，若开始，则各变量恢复为前一次优化收敛时的保存值，并减小收缩因子，转步骤（3）；否则，继续。

　　（10）约束潮流不收敛，不能进行优化，结束。

　　（11）输出优化结果，结束。

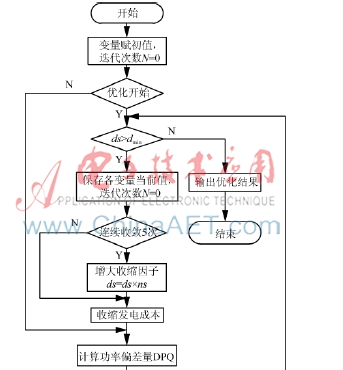
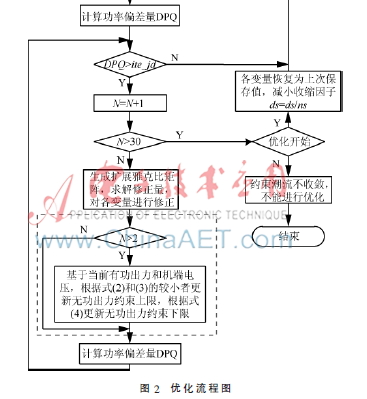
　　优化流程如图2，图中虚线框内部分对应步骤（9），表示考虑发电机安全运行极限后，在优化过程中即时更新发电机无功出力约束限值。

　　其中N为约束潮流迭代次数，DPQ为最大功率不平衡量，ite_jd为潮流收敛精度，这三个量与常规潮流计算中的意义相同。ds为收缩因子，dmin为收缩因子的收敛阈值，ns为收缩比，这三个量为基于函数变换与广义逆的优化算法的特有参数。

5 算例分析

　　选取IEEE57系统[10,11]为算例，对本文研究进行分析。为验证优化中考虑发电机安全运行极限的必要性，将系统中发电机节点2的无功负荷增加1(p.u.)。文中收缩因子初值取ds=103，收敛阈值取dmin=10-6，收缩比取ns=2，内层循环约束潮流计算的收敛判据取功率偏差量DPQ＜10-6。

　　5.1 有功/无功协调优化效果分析

　　5.1.1 分别进行有功优化和无功优化

　　先不计网损，按等耗量微增率准则进行有功优化，确定各发电机节点的有功出力计划值；在此基础上进行潮流计算，以得到计入网损后平衡节点1的有功出力值，如表1所示。其中计入网损后增加的发电成本即为对应于网损的费用。

　　除平衡节点1外其余发电机节点有功出力保持不变，不计发电机安全运行极限，进行无功优化，结果如表2所示。可见，优化后只有平衡节点1的有功出力随网损降低而减少，从而引起发电成本的降低。其余发电机节点由于有功出力不变，不能对发电成本降低有所贡献。

　　5.1.2 有功/无功协调优化

　　采用本文所述模型，计及发电机安全运行极限进行有功/无功协调优化，优化结果如表3所示。

　　对比表2和表3可见，有功/无功协调优化相对于分别进行有功优化和无功优化，有如下特点：

　　（1）经济性最好的节点1有功出力略有下降，经济性最好的节点8和经济性稍差的节点2、9和12有功出力略有上升，这可能引起发电成本上升。

　　（2）节点1远离负荷中心，而其他节点离负荷中心较近，节点1的出力下降和其他节点的出力上升，都会使得线路输送功率减少，导致网损降低，从而使发电成本得以降低。

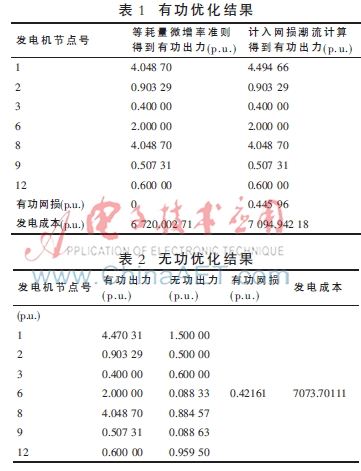
　　以上两种情况相互协调，最终使得有功/无功协调优化可以得到更低的发电成本。对比表1和表3，注意到有功/无功协调优化后的发电机有功出力，相对于有功优化后的有功出力计划值变化不大，经济性最差的节点3始终保持为最低有功出力，这在一定程度上保证优化后的经济性不致于降低。

　　5.2 发电机安全运行极限的影响分析

　　5.2.1 优化过程比较

　　进行电力系统有功/无功协调优化时，发电成本随优化过程变化曲线如图3所示。

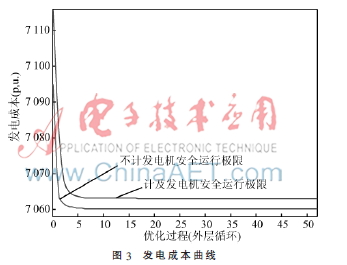
　　由图3可以直观的看出，不论是否计及发电机安全运行极限，算法优化性能良好，优化过程5后，发电成本已非常接近最优结果。但计及发电机安全运行极限后优化效果略差，原因分析见5.2.2节。

　　5.2.2 发电机无功出力分析

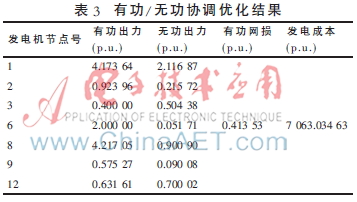
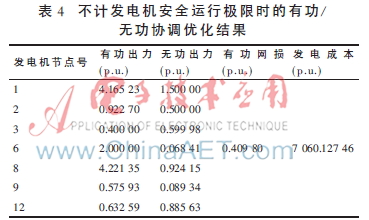
　　不计发电机安全运行极限时，有功/无功协调优化结果如表4所示。其中有功网损和发电成本均低于表3中计及发电机安全运行极限时的优化结果,与图3结论相符。

　　若考虑发电机安全运行极限，发电机无功出力约束限值并非定值，而是变化的，优化结束后，各发电机的实际无功出力约束限值如表5所示。

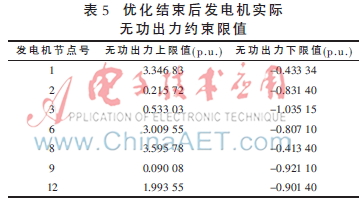
　　对比表4和表5中无功出力数据可见，不计发电机安全运行极限时，节点2和3无功出力已越上限，所以其优化效果看似更好，但实则是以牺牲发电机的安全运行为前提的，是一种不可取的运行状态。这证明了进行电力系统有功/无功协调优化时考虑发电机安全运行极限是很有必要的。

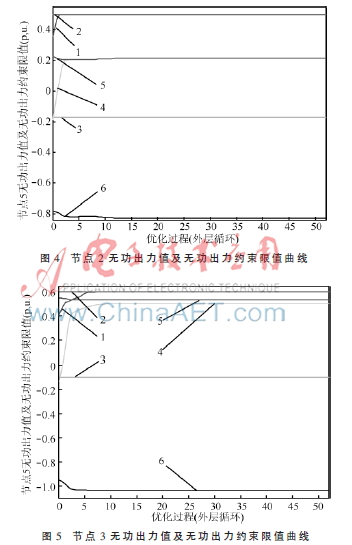
　　图4和图5表示的是优化过程中节点2和节点3的无功出力及其约束限值变化曲线，可直观地看出不计发电机安全运行极限时两节点无功出力的越上限情况，而计及发电机安全运行极限时，两节点无功出力始终在其约束范围内。

　　5.3 发电机经济参数影响分析

　　发电成本与机组的经济参数有直接关系。本节选定系统中远负荷点1和近负荷点9为试验节点，对其经济参数做出相应改变，并进行计及发电机安全运行极限的电力系统有功/无功协调优化。优化结果如表6所示（发电成本随经济参数变化而变化，不具可比性，因此下表着重比较优化后的机组有功出力值随发电机经济参数的变化）。

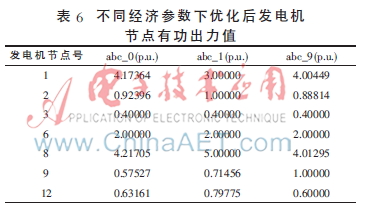
　　比较abc_0和abc_1，远负荷点1的经济性变差，其有功出力降低为其下限值，以降低发电成本，同时离负荷点相对较近的其他发电机节点的有功出力则增加，使得线路输送功率减少，降低网损，这会使发电成本进一步降低。

　　比较abc_0和abc_9，近负荷点9的经济性变好，其有功出力增加为其上限值，其他发电机节点有功出力略有减少，同时近负荷点出力的增加也会减少线路输送功率，使网损降低，这一系列变化的综合作用最终会使得发电成本降低。

　　同时还注意到，经济性最差的节点3和经济性稍差的节点6的有功出力基本保持为其下限值，以避免其出力过多而造成发电成本的上升。

6结论

　　电力系统有功/无功协调优化，相对于先有功优化后无功优化的传统方式，距离负荷中心远近不同且经济性能不同的机组有功出力调节更加灵活，优化后的发电机有功出力受该节点距离负荷中心远近及机组经济参数的影响，二者相互协调，最终达到发电成本最低的最佳状态。

　　考虑发电机安全运行极限，可以使发电机始终运行在安全区域内，得到更符合实际的优化结果。

参考文献

　　[1]周晓娟,蒋炜华,马丽丽. 基于改进遗传算法的电力系统无功优化[J]. 电力系统保护与控制, 2010, 38(7): 37-41.

　　[2]曾嘉俊,刘志刚,何士玉,等. 一种基于子区域粒子群的无功优化算法研究[J]. 电力系统保护与控制, 2012, 40(1): 37-42.

　　[3]孙伟卿,王承民,张焰,等. 电力系统综合节能的有功与无功功率协调优化[J]. 电机与控制学报, 2010, 14(7): 41-47.

　　[4]丘文千. 具有变量范围约束的潮流算法在OPF中的应用[J]. 电力系统自动化, 2007, 31(15): 35-40.

　　[5]陈珩. 电力系统稳态分析（第三版）[M]. 北京: 中国电力出版社, 2007: 17-18.

　　[6]ADIBI M M, MILANICZ D P. Reactive Capability Limitation of Synchronous Machines[J]. Power Systems, IEEE Transactions on, 1994, 9(1): 29-40.

　　[7]NILSSON N E, MERCURIO J. Synchronous Generator Capability Curve Testing and Evaluation[J]. Power Delivery, IEEE Transactions on, 1994, 9(1): 414-424.

　　[8]ROSEHART W D, CANIZARES C A, QUINTANA V H. Effect of Detailed Power System Models in Traditional and Voltage-stability-constrained Optimal Power-flow Problems[J]. Power Systems, IEEE Transactions on, 2003, 18(1): 27-35.

　　[9]鲍海波,韦化. 考虑发电机运行极限的电压稳定临界点互补模型与算法[J]. 电力系统自动化, 2012, 36(22): 12-18.

　　[10]吴际舜,侯志俭. 电力系统潮流计算的计算机方法[M].上海:上海交通大学出版社, 2000.

　　[11]余娟. 无功优化新模型和算法研究及其在电压稳定风险评估中的应用[D].重庆:重庆大学, 2007.