黄剑雄，谢伙生

　　（福州大学 数学与计算机学院，福建 福州 350116）

       摘要：由于高效用模式挖掘较为复杂，提高其挖掘算法的效率是数据挖掘的研究热点。HUPminer算法是典型的基于垂直模式类的高效用模式挖掘算法，虽然能够有效地减少效用列表的总个数，但对于项集的划分，效用列表需要更多的空间。针对该问题，在HUI-miner算法的基础上充分考虑了1扩展集中项集的关联性，减少了效用列表个数，提出了改进的IHUI-miner算法。实验结果表明，改进算法IHUI-miner在时间效率和减少效用列表的个数上都优于HUP-miner与HUI-miner算法。

　　关键词：高效用模式；频繁模式；频繁项集；垂直模式

　　中图分类号：TP311.13文献标识码：A DOI： 10.19358/j.issn.16747720.2016.22.006

　　引用格式：黄剑雄，谢伙生. 垂直模式类高效用模式挖掘的改进算法［J］.微型机与应用，2016,35（22）：22-25.

0引言

　　近年来，高效用模式挖掘是频繁模式挖掘研究的热点之一。与传统的频繁模式相比，高效用模式挖掘中每条事务的项都有对应的值（如数量），同时项集的每个项也有对应的值（如利润），其目标就是寻找所有效用值大于或等于最小效用值的项集。传统频繁模式挖掘是利用向下闭合的性质来减少挖掘过程中的空间搜索时间，而高效用模式挖掘是利用事务权重效用值TWU（Transaction Weighted Utility）性质［1］来减少搜索时间。

　　高效用模式挖掘算法主要有模式增长类与垂直模式类算法。TWO-Phase算法［1］是最早运用模式增长方式来实现高效用模式挖掘的，需要花费大量的时间和空间来产生候选集和计算实际效用值。大多数的高效用事务数据集只能有损地存储在树结构中，这也是模式增长类算法IHUP［2］、UP-Growth［3］和UP-Growh+［3］的改进目标，是减少候选集产生的关键所在，文献［4］提出了垂直模式类高效用模式挖掘的HUI-miner算法，该算法与Eclat算法类似，能直接计算项集的实际效用值，每个项集拥有一个效用列表UL（Utility List），用来构造其他项集的效用列表和计算实际效用值，并利用TWU性质来剪枝。HUI-miner算法优于模式增长类的IUPTWU算法、UP-Growh+算法。文献［5］提出了垂直模式类的HUP-miner算法，该算法提出了划分效用列表PUL(Partitioned Utility List)，每个PUL由项集的效用列表UL和划分列表PL（Partition List）组成，一方面利用PU-Prune性质［5］和划分列表来预判断是否需要构造项集的效用列表，另一方面在构造PUL过程中，利用LA-Prune性质［5］来及时判断返回而不是等到构造完成后再返回，以此来减少效用列表的数目，提高算法效率。尽管如此，HUP-miner算法还是存在一些值得改进的地方，具体体现在：（1）在利用PU-Prune性质和划分列表进行预判断时，若最小效用值较小或数据集较密集，则可能会存在过多的冗余计算和内存消耗。（2）在利用LA-Prune性质来减少项集效用列表的构造过程中，忽略了同一项集的1 扩展集中项集之间的关联性。针对这些不足，本文提出了一个改进的高效用模式挖掘的改进算法IHUI-miner(Improved High Utility Itemsets)，该算法仍沿用HUI-miner中的效用列表来存储数据集，以更新保留项集的效用列表剩余效用值，同时对HUP-miner中LA-Pruning策略进行扩展。实验结果表明，IHUI-miner算法在时间效率和减少列表的个数上都优于HUP-miner与HUI-miner算法。

1相关定义与性质

　　假设I={i1,i2,…,im}是由m个不同项组成的项集合，每项ik(1≤k≤m)都有一个称为外效用的值，记为EU(ik)。D={T1,T2,…,Tn}是长度为n的事务数据集，D中的每个事务Tb(1≤b≤n)都是项集I的子集，都有一个唯一的标识符（TID）b。事务Tb中的每个项ic都有一个称为内效用的值，记为IU(ic,Tb)。若项集P是一个长度为L的项集，称P为L项集；Pik（ik∈I）以P为前缀，长度为L+1的项集，称Pik为P的1 扩展项集。

　　定义1项ik在事务Tb中的效用值记为U(ik,Tb)，其定义如下：

　　U(ik,Tb)=EU(ik)*IU(ik,Tb)

　　定义2项集X在事务Tb中的效用值记为U(X,Tb)，其定义如下：

　　U(X,Tb)=∑ik∈X,XTbU(ik,Tb)

　　定义3项集X在D中的效用值记为U(X)，其定义如下：

　　U(X)=∑XTb,Tb∈DU(X,Tb)

　　定义4一个事务Tb的效用值指的是事务Tb中所有项的效用值之和，记为TU(Tb)，其定义如下：

　　TU(Tb)=∑ik∈TbU(ik,Tb)

　　定义5项集X在数据集D中的事务权重效用值TWU指的是事务数据集D中包含X的所有事务效用值之和，记为TWU(X)，其定义如下：

　　TWU(X)=∑XTb,Tb∈DTU(Tb)

　　定义6X为任意给定的项集，minutil为用户给定的最小效用值（下同），若U(X)≥minutil，则称项集X是高效用项集HUI；否则，项集X为非高效用项集。

　　定义7在事务Tb中，项集X之后的项组成的集合记为Tb/X。

　　定义8项集X在事务Tb中的剩余效用值RU(Remaining Utility)记为RU(X,Tb)，其定义如下：

　　RU(X,Tb)=∑ik∈Tb/XU(ik,Tb)

　　定义9如果项集有完成构造效用列表，则称该项集为保留项集，否则称为非保留项集。

　　TWU性质:对任意给定的项集X，若TWU(X)<minutil，则项集X的任意超集都不是高效用项集。

　　性质1已知在P的1 扩展集中保留项集的集合为Q={Pi′1,Pi′2,…,Pi′k}，则有对任意的1≤j≤k，Pi′jTb，RU(Pi′j,Tb)更新为∑km=j+1U(i′m,Tb)。

　　显然可以证明更新后的RU(Pi′j,Tb)不会影响项集的生成，即若有U(Pi′j)+RU(Pi′j)<minutil，则以Pi′j为前缀的所有扩展集都不是高效用项集。

　　由性质1对LA-Prune性质［3］进行进一步扩展可得到性质2。

　　性质2已知在P的1扩展集中，保留项集的集合为Q={Pi′1,Pi′2,…,Pi′k}， Tb∈D，Pi′m,Pi′n∈Q(m<n)，在构造Pi′mi′n的效用列表过程中，若∑Pi′mTb,Pi′nTb(U(Pi′m,Tb)+RU(Pi′m,Tb)－(RU(Pi′n,Tb)－RU(Pi′mi′n,Tb))<minutil，则不必构造Pi′mi′n的效用列表（其中RU(Pi′mi′n,Tb)为性质1更新后的值）。

2IHUI-miner算法

　　改进算法IHUI-miner仍沿用HUI-miner中的效用列表进行存储，每个效用列表由元素<TID，U，RU>组成。虽然在生成项集的1扩展集时，HUPminer算法有判断是否需要生成该扩展集的效用列表，但未对保留项集效用列表中元素对应的RU进行更新。IHUI-miner算法不仅对1 扩展集中的保留项集效用列表中的每个元素的RU值进行更新，同时对HUP-miner中的LA-Pruning策略进行了扩展。IHUI-miner算法仍沿用HUP-miner的方式来对空间进行搜索，第一次扫描得到所有项的TWU值；第二次扫描构造所有TWU值大于minutil的项的效用列表ULs，通过调用搜索算法Search space（null，ULs，minutil)来输出所有高效用项集。

　　改进算法： IHUI-miner

　　输入:事务数据库D;

　　用户最小效用值minutil;

　　1.扫描D的所有事务，计算所有项的TWU值；

　　2.for D中的每个事务Tb do

　　3.对Tb中的项ik按TWU值降序排序；

　　4. 扫描排序后的Tb，构造项的效用列表ULs；

　　5. End

　　6. Searchspace （null，ULs，minutil); //算法1

　　2.1空间的搜索

　　改进算法IHUI-miner的空间搜索过程如算法1所示。采用深度优先的递归方式来生成项集的1 扩展集，从前往后依次取效用列表X作为前缀（第1行），如果U(X)≥minutil，则输出X（第2~4行），随后实现TWU性质的判断（第5行）。由于项集X效用列表的TID集包含其扩展集X、Y的所有TID，取大小为X.size用来更新保留项集每个TID的RU值（第8,9行）。为了了解其后的项集是否为保留项集，从后往前得到后缀Y（第10行）；在构造过程中，head保存着上一个保留项集中每个TID的RU值，tail保存着本次每个TID的RU值，其原因是并不知道本次是否会完成构造效用列表，如果没有，则head依然是最新的值，否则利用tail来对head进行更新（第15行）。为了保证1扩展集中的次序，在存储效用列表时，采用了相反的顺序（第14行）。在下次递归之前提前回收head和tail的内存（第18行）。

　　算法1: Search space(ULP,ULs，minutil)

　　输入:项集P的效用列表ULP，初值为null；

　　项集P的1 扩展效用列表集ULs，初值为项的效用列表；

　　用户给定的最小效用值minutil；

　　输出：所有的高效用项集；

　　1. for ULs中的每个效用列表X do

　　2.if U(X) ≥ minutil then

　　3.输出项集X ;

　　4.end

　　5.if U(X) + RU(X) ≥ minutil then

　　6.exULs = {} ;

　　7. /*性质1*/

　　8.head指向大小为X.size的空间;初始化为0;

　　9.tail指向大小为 X.size的空间;

　　10.for ULs中最后一个到X+1的每个效用

　　列表Y do

　　11.ULXY = ConstructUL (ULP,X,Y，head，

　　tail, minutil) ; //算法2

　　12. if ULXY≠ NULL then

　　13./*性质1*/

　　14.ULXY插到exULs的前端 ;

　　15.head <－> tail ;

　　16. end

　　17. end

　　18.head = tail = null ;

　　19. Searchspace (X, exULs, minutil)

　　20. end

　　21. End

　　2.2效用列表的构造过程

　　效用列表的构造过程包括项集的效用值的计算及效用列表的构造，如算法2所示。在构造过程中，从头到尾扫描效用列表Px的每个元素位置pos（第3行），在效用列表Py寻找相同的事务TID的元素（第6行），计算该项集的最后一个项y在每个事务中的值（第7行），所以tail的值可以由该值和head中的值来更新（第9,12行），同时用head来更新项集效用列表中每个TID的RU值（第8，11行）。设Pxy的TWU初值取Px的TWU值（第2行），用于在构造过程中不断地去逼近项集Pxy的TWU值。每次先减去事务中其后非保留项集最后一项的值（第15行），再利用性质2进行判断（第20行）。

　　算法2:ConstructUL Algorithm

　　输入：项集P，Px，Py的效用列表ULP,ULPx,ULPy；

　　数组指针head，tail；

　　用户给定的最小效用值minutil；

　　输出：项集Pxy的效用列表ULPxy；

　　1.ULPxy= NULL

　　2.TWU_PX= U(Px) + RU(Px)//性质2的初值

　　3.for ULPx中的每个元素位置posdo

　　4. if Ey∈ULp and ULPx［pos］.TID == Ey.TID

　　then

　　5. ifULP ≠ NULL then

　　6. ULP中找元素E使得E.TID == Ey.TID ;

　　7.y_utility= Ey.U-E.U;

　　8.Exy=<Ey.TID,ULPx［pos］.U+

　　y_utility,head［pos］> ;/*性质1*/

　　9. tail［pos］ = head［pos］ + y_utility ;

　　10. else

　　11.Exy=<Ex.TID,Ex.U +Ey. U,head［pos］> ; /*性质1*/

　　12.tail［pos］=head［pos］ + Ey. U;

　　13. end

　　14. 将元素Exy添加到ULPxy;

　　15.TWU_PX -= (Ry.RU - head［pos］) ; /*性质2*/

　　16. else

　　17.TWU_PX -= (Rx.U + Rx.RU) ;

　　18.tail［pos］ = head［pos］ ;

　　19. end

　　20. if TWU_PX < minutil then

　　return NULL ;/*性质2*/

　　21 .end

　　22.returnULPxy

3实验结果

　　通过与HUP-miner和HUI-miner的实验对比来测试新算法的性能，计算机的配置为Inter Core i53470 3.20 GHz CPU、16 GB内存、Windows 7 64位系统，三个算法均用Java来实现，其中HUI-miner与HUP-miner的算法代码来源于SPMF［6］，HUP-miner算法K值取为512。

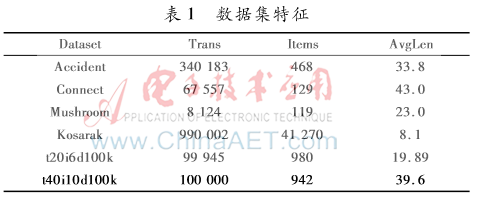
　　实验所用的数据来源如表1所示，总共有6个数据集，其中Accident、Connect、Mushroom、Kosarak为实测数据［6］；t20i6d100k和t40i10d100k为合成数据，取自FIMI库［7］，内效用值在1~10之间随机产生，外效用值采用log正态分布。

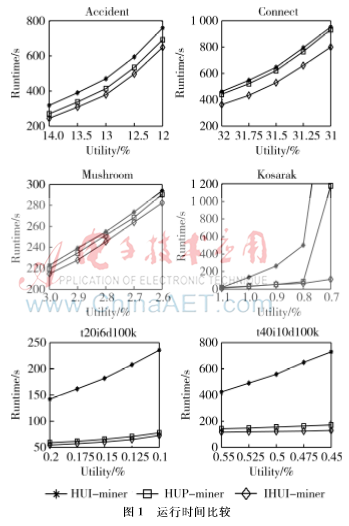
　　算法的运行时间比较如图1所示，从图中可以看出，IHUI-miner算法在运行时间上优于HUI-miner算法和HUP-miner算法。当数据集kosarak取值为0.7时，HUP-miner算法花费的时间是IHUI-miner时间的近10倍，这主要是因为该数据集中在minutil值的变化时，高效用项集的数目并未有很大的浮动；minutil的值减少，HUP-miner效用列表所占的比例并未有明显的下降，效用列表的数目不断增加，而IHUI-miner算法所占的比例不断下降，并逐渐趋于0。

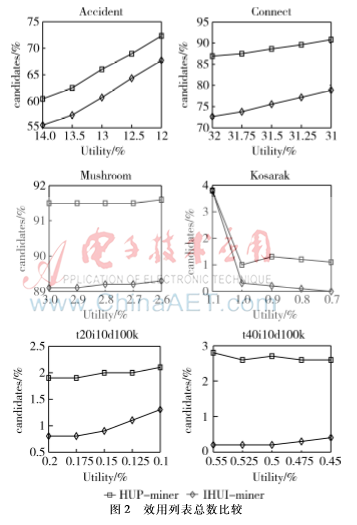
　　算法的效用列表总数比较如图2所示，图中纵轴表示IHUI-miner算法、HUP-miner算法的效用列表总数与HUI-miner算法的效用列表总数的百分比。实验结果表明，IHUI-miner算法的效用列表总数明显小于HUP-miner算法，两者的效用列表总数都小于HUI-miner算法（小于100%），表1中的后三个测试数据集最为明显。

4结论

　　本文对垂直模式类的高效用模式挖掘的HUI-miner与HUP-Mine算法进行了分析总结，针对该类算法的不足，给出了扩展项集的两个性质，在此基础上提出了一个改进的IHUI-miner高效用模式挖掘算法，该算法构造的效用列表的项集是HUP-miner算法的子集，降低了效用列表的总数，去除了HUP-miner的PUL的划分列表，理论分析与实验结果都表明，改进算法IHUI-miner在时间和列表个数上都优于HUP-miner与HUI-mine算法。

　　参考文献

　　［1］ Liu Ying, Liao Weikeng, CHOUDHARY A. A two phase algorithm for fast discovery of high Utility Itemsets［J］. 9th Pacific Asia Conference on Advances in Knowledge Discovery and Data Mining (PAKDD), Hanoi, Vietnam, 2005, 3518:689-695.

　　［2］ AHMED C F, TANBEER S K, JEONG B S, et al.Efficient tree structures for high utility pattern mining in incremental databases［J］. IEEE Transactions on Knowledge and Data Engineering, 2009, 21(12):1708-1721.

　　［3］ TSENG V S,SHIE B E,WU C W, et al. Up growth：an efficient algorithm for high utility itemsets mining［C］ .16th ACM SIGKDD International Conference on Knowhedge Discovery and Data Mining (KDD), Washington,2010 :253262.

　　［4］ Liu Mengchi, Qu Junfeng.Mining high utility itemsets without candidate generation［C］. ACM international conference on Information and knowledge management, 2012:55-64.

　　［5］ SRIKUMAR K. Pruning strategies for mining high utility itemsets［J］.Expert Systems with Applications 2015, 42(5):2371-2381.

　　［6］ FOURNIER VIGER P, GOMARIZ A, LAM H, et al. Spmf: opensource data mining platform［EB/OL］.（2015-12-13）［2016-08-15］http://www.philippefournier  viger.com/spmf.

　　［7］ Frequent itemset mining dataset repository［EB/OL］.（2015-12-31）［2016-08-15］http：//fimi.ua.ac.be.