文献标识码: A
DOI:10.16157/j.issn.0258-7998.2017.01.038
中文引用格式: 潘振福,许静,刘成,等. 基于视觉目标跟踪的PTZ控制方法[J].电子技术应用,2017,43(1):145-147.
英文引用格式: Pan Zhenfu,Xu Jing,Liu Cheng,et al. The method of controlling PTZ camera based on visual object tracking[J].Application of Electronic Technique,2017,43(1):145-147.
0 引言
PTZ(Pan/Tilt/Zoom)摄像头是将CCD摄像机、变焦变倍镜头、全景云台等部件集成在一个单元中构成的摄像机系统。传统的PTZ摄像机监控系统通过人工操控键盘或者摇杆对监控目标进行跟踪,如果目标较远,通过手动控制镜头变焦,这种人工操控的方式跟踪误差太大,造成系统摄像不稳定、不连续。近年来,基于主动视觉的PTZ摄像机系统逐渐发展,陈双叶等人提出基于Camshift算法和卡尔曼滤波器目标跟踪算法的PTZ摄像机控制方法[1],简单地采用颜色直方图作为跟踪匹配特征,容易受到光照变化、运动模糊遮挡等因素影响而造成跟踪失败。WANG S等人提出的高斯混合模型目标检测定位方式的PTZ控制方法仅仅解决了镜头对焦问题[2]。而DONG E等人除了应用高斯混合模型目标检测之外,还融合了Kalman滤波器与Camshift算法对目标进行跟踪,从而控制PTZ摄像机[3],相比近年来先进的目标跟踪技术,这些跟踪算法相对落后,其性能容易受众多因素影响,包括光照变化、遮挡和背景混杂等。在视觉目标追踪(The Visual Object Tracking,VOT)2014年挑战结果[4]中显示,基于分类相关滤波器的跟踪器是目前最优秀的目标跟踪算法之一,提供了先进的跟踪性能。HENRIQUES J F等使用了梯度方向直方图(HOG)特征,提出了核相关滤波器(Kernelized Correlation Filter,KCF)及双相关滤波器(Double Correlation Filter,DCF)跟踪器[5],运算速度能达到300 b/s以上。
本文采用KCF目标跟踪方法作为控制算法核心对运动目标进行跟踪,并采用粒子滤波框架对目标进行运动状态预测,根据跟踪结果使用PID算法对PTZ摄像机进行协调控制。
1 PTZ摄像机系统架构
本文中的PTZ摄像机系统由云台摄像机、视频采集卡以及运行PTZ控制系统的上位机组成,如图1所示。

由视频采集卡从摄像头采集回来的图像传入算法中进行跟踪运算,通过RS232转RS485串口遵循PELCO-D协议控制PTZ摄像机转动,保持跟踪目标在视频图像中。PELCO_D协议定义了水平旋转、上下旋转、变焦变倍等功能。
2 目标跟踪方法
在KCF跟踪算法中,以核岭回归分类器作为核心,用循环移位方法致使样本变换,建立循环矩阵来训练该分类器,然后把目标与周围背景区分开来,从而达到对目标快速有效检测跟踪的目的。对样本进行巧妙地变换使训练数据矩阵具有循环特性,就可以通过离散傅里叶变换对角化,便能减少几个数量级的存储与计算,这就是文献[5]提出的核岭回归相关滤波器(Kernelized Correlation Filter,KCF),具有其他核算法没有的线性复杂度。
2.1 岭回归分类器
针对线性岭回归判别函数f(z)=wTz,训练的目的是利用样本xi找到一个权值wi对回归目标yi最小平方误差:

其中λ是正则化参数,控制过度拟合。根据文献[6]得到最优解:

由式(4)可知,需要优化的变量是α,而并不是w。
核岭回归问题的解由文献[9]给出:

2.2 循环矩阵
对样本x进行移位变换,可以获得循环矩阵X,即:
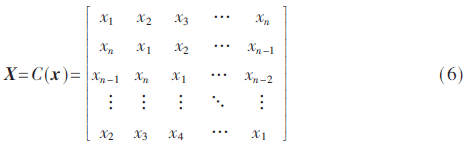
矩阵X完全由指定的样本向量x(这里的第一行)循环移位生成。无论生成向量x为何值,所有循环矩阵都能被离散傅里叶变换(DFT)矩阵对角化[10]。也就是:

2.3 核相关分类器训练
只要满足文献[5]提出的定理1的核函数的核矩阵K具有循环结构,所以:

2.4 目标快速检测
为了检测出感兴趣物体,通常用回归函数f(z)去评估目标在多个图像中位置信息,从而估计出目标位置。把包含目标图像且比目标尺寸大的图像块作为搜索窗口,对此搜索窗口进行循环移位,形成不同的候选图像块,然后建模成循环结构的循环矩阵。
假设核矩阵Kz由匹配模板和搜索窗口样本核相关所得。因为匹配模板X和检测样本Z是基于元素向量x和z移位变换的循环结构矩阵,相应的,Kz的每个元素是由κ(pi-1z,pj-1x)组成,根据文献[5]的定理1可以验证这个矩阵是一个循环核矩阵。与上一节相似,只需第一行元素来表示核矩阵:

其中kXZ是前面定义的x与z的核相关运算。可以把回归函数表示为:

注意到f(z)是一个矩阵元素z向量的所有移位变换形式的输出响应,为了更有效地计等式(13),得到对角化后的等式:

3 实验分析
在QT5平台上完成PTZ摄像头系统上位机端的C++实现,运用了OPENCV库。
3.1 跟踪质量评估
在实验室环境下,运行结果如图2所示,运动目标被完全遮挡的情况下,跟踪算法仍然很稳定。

3.2 PTZ控制质量实验
上位机通过RS232转RS485转串口与PTZ摄像头相连,遵循PELCO_D协议控制。控制结果如图3所示。图中中间位PTZ摄像头贴有白色的标识,以便明显看到其转动,图中右下角为摄像头跟踪的图像。结果显示,其能始终保持跟踪目标在图像中。

4 结论
针对目前现有的主动视觉的PTZ摄像头控制系统的跟踪性能较差、导致跟踪丢失等问题,提出了一种基于核相关视觉目标跟踪器的PTZ摄像机控制方法,并在QT平台上应用OPENCV库实现了PTZ摄像机控制系统的C++版。实验结果验证了本系统的稳定性与鲁棒性。
参考文献
[1] 陈双叶,王善喜.PTZ摄像机跟踪运动目标的智能控制算法的研究[J].计算机科学,2015(S2):135-139.
[2] WANG S,TIAN Y,XU Y.Automatic control of PTZ camera based on object detection and scene partition[C].IEEE International Conference on Signal Processing,Communications and Computing.IEEE,2015.
[3] DONG E,YAN S,TONG J,et al.Design and implementation of a moving object tracking system[C].IEEE International Conference on Mechatronics and Automation.IEEE,2015.
[4] KRISTAN M,PFLUGFELDER R,LEONARDIS A,et al.The visual object tracking VOT2014 challenge results[C].Lecture Notes in Computer Science,2014:191-217.
[5] HENRIQUES J F,CASEIRO R,MARTINS P,et al.High-speed tracking with kernelized correlation filters[J].IEEE Transactions on Pattern Analysis & Machine Intelligence,2014,37(3):1-1.
[6] RIFKIN R,YEO G,POGGIO T.Regularized least-squares classification[J].Nato Science Series Sub Series III Computer and Systems Sciences,2003,190(1):93-104.
[7] MULLER K R,MIKA S,TSUDA K.An introduction to kernel-based learning algorithms[J].IEEE Transactions on Neural Networks,2001,12(2):181-201.
[8] SCH?魻LKOPF B,SMOLA A.Learning with kernels:Support vector machines,regularization,optimization,and beyond[M].MIT Press,2002.
[9] RIFKIN R,YEO G,POGGIO T.Regularized least-squares classification[J].Acta Electronica Sinica,2003,190(1):93-104.
[10] GRAY R M.Toeplitz and circulant matrices:a review[M].Now Publishers,2006.
作者信息:
潘振福,许 静,刘 成,朱永利
(华北电力大学 计算机系,河北 保定071003)

