陈德华,洪灵涛,潘乔
(东华大学 计算机科学与技术学院,上海 201620)
摘要:糖尿病在治疗过程中,其生化检验指标的变化受患者基本特征、指标等影响。文中针对预测患者糖尿病生化指标的问题,结合神经网络等机器学习方法,构建了一个基于改进神经网络的糖尿病生化指标预测模型。该模型考虑了糖尿病生化指标和患者的基本特征对指标的影响,同时又将患者之前的检验数据样本加入到模型中。实验证明,对于糖尿病患者的指标数据,3个主要血检指标预测训练集的R2值达到0.772 1、0.551 8、0.706 3,测试集的R2值达到了0.644 7、0.584 0、0.804 6,对比实验也证明了该模型相较于常用的机器学习模型有着更好的预测效果。
关键词:糖尿病;神经网络;指标预测
中图分类号:TP302文献标识码:ADOI: 10.19358/j.issn.1674-7720.2017.05.017
引用格式:陈德华,洪灵涛,潘乔.基于改进神经网络的糖尿病生化指标值预测[J].微型机与应用,2017,36(5):54-56,59.
0引言
糖尿病作为一个高发的内分泌疾病,其各项指标的预测都有很重要的意义。糖化血红蛋白(HbA1c) 指标是人体血液中红细胞内的血红蛋白与血糖结合的产物, 通常可以反映患者近8~12周的血糖控制情况;空腹血糖(Glu)指标能够代表基础胰岛素的分泌功能;而胰岛素释放试验(Ins)反应了胰β细胞的储备功能,这些糖尿病的主要指标预测具有调整治疗方案、评估患者状态、衡量治疗结果等重要的实际意义。
以往糖尿病的指标预测仅仅停留在医学领域或者简单的统计分析上。随着机器学习技术的发展,各类机器学习模型也被应用到医疗行业的各个领域。但是对于大量有不同特性的数据样本,许多机器学习的模型过于泛用,而对于糖尿病指标数据的预测而言,以往的模型大多停留在解决指标间的相关性上,而没有考虑到患者一直以来的指标变化。同时患者指标变化数据具有不规则时序特性,这些特性也阻碍了一些模型应用到这类特殊的数据集上。
本文提出了一个基于改进神经网络的模型,该模型不仅充分考虑到患者指标间的相互影响,同时通过加入隐藏层来拟合患者多次检查中不规则的时序特性,对比实验也证明了该模型相较于常用的机器学习模型有着更好的预测效果。
1糖尿病临床数据建模
糖尿病临床数据主要由两部分组成:患者的基本信息,此维数据主要包括了患者的性别、年龄、妊娠状态等;患者的检验数据,此维数据主要包括了患者历次的各项生化指标的检验时间和指标值。
由以上两类数据源可以得到一个以患者、时间和患者属性(包括患者特征和指标等)为3个维度的三维数据模型,而这个数据模型有以下特点:
(1)不规则的时序特性
例1.表1中列举了一个患者血液检查中糖尿病主要指标的数据样本。该数据的时间跨度从2011年~2012年,共有5次检查数据,每次检查与上一次检查的时间间隔分别为110天、103天、128天和60天。
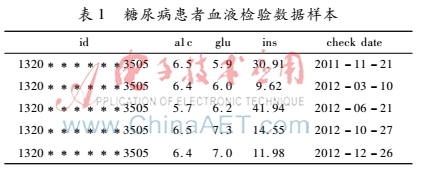
例1中可以看到,医疗数据的确具有时序特性,但相较于标准的或者较为正规的时序数据集,医疗数据的时序点更为残缺和稀疏。这就使得很多数学模型并不适用于真实医疗数据的预测。
(2)指标和患者基本信息具有相关性
例2. 表2为不同性别分组A1C指标的统计描述。展示了不同年龄和性别分组的情况下患者的A1C指标分布情况。从例2中可以看出,不同性别的患者指标分布并不均匀,同时患者的年龄对指标的分布也有着影响。
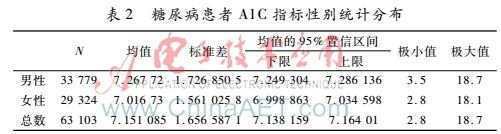
(3)指标间具有相关性
患者的指标存在相互影响的关系,相关资料也表明,患者的疾病指标也与很多的患者特性有着诸多相关,所以指标间的相互影响不可忽略。
2神经网络及存在的不足
BP神经网络[1 2]是一种按误差逆传播算法训练的多层前馈网络,是目前应用最广泛的神经网络模型之一。神经网络擅长于处理内部机制复杂的问题,具有较强的非线性映射能力,因而神经网络在处理指标间、患者基本属性与指标预测的关系时有较强的能力[3]。但是,由于需要同时考虑到患者多次检查对患者指标的影响,一般的神经网络无法处理多次输入之间的关系,不能很好地适应当前的数据模型。因而为了较好地预测糖尿病患者的几个主要指标变化,提高预测精确度,本文利用糖尿病患者特征、治疗时间和治疗过程中的指标变化特性,提出了一个基于神经网络的改进神经网络模型,利用了BP神经网络[2 3]中的思想,来完成糖尿病指标的预测。
3预测模型架构
根据上节的描述,考虑到患者的各种特征对指标预测的影响,将患者性别、年龄、妊娠状态等也作为模型的输入。同时,如例1种所述,考虑到医疗数据所具有的时序特性,本文在改进的模型中加入了一个隐藏层,用于保存上一次隐层的输出,并将它用于下一次的隐层计算,以此来拟合医疗数据的时序特性。为了简化部分计算,减低模型可能的过拟合概率,模型将一些与预测结果直接相关的输入单独列出,作为特殊的节点输入,直接连接到输出节点。
3.1模型描述
实验中的模型是基于BP神经网络改进的,具体包括4个层次,即输入层、隐藏层1、隐藏层2和输出层次。
将输入参数x1,x2,…,xn记作x,对输入参数先进行线性变换,对于隐层1节点j的输入有:

其中ωTj表示连接输入层和隐层1节点j的权值向量,ωi→j表示输入层节点i到隐层j的权值,n表示输入层节点数量。
隐层中激励函数选用sigmoid函数,所以为了保证sigmoid有较好的感知效果,本文利用sigmoid在定义域为0附近较为敏感的特性,结合数据特点,将式(1)中的kj进行双曲变换,然后再附上偏置量,由此得到隐层的激励函数为:
![_@{S43L}}EC`[6S]2A[OYG5.png _@{S43L}}EC`[6S]2A[OYG5.png](http://files.chinaaet.com/images/2017/04/07/6362716384665684358787926.png)
其中pi表示隐层1节点i的输出,βi为对应偏置量。
隐层2的节点i保存着上一次隐层1节点的输出,将隐层的节点i输出记作yi,隐层2的节点i所保存的值记作y′i(注:隐层1、2的节点数相同),则对于隐层节点i的实际输出有:
yi=pi+αiy′i(3)
其中αi表示隐层2节点i所对应的输出权值。
对于输入层中包含特殊节点N,笔者认为在这样一份时序数据中,每条数据的时间与其输出有直接关系,则不将该节点通过隐层处理,而是直接连接到输出层。将隐层的输出y1,y2,…,yn记作y,在输出层采用purelin函数,可以得到输出层的输出zj为:
zj=υTj·y+γj·g+bj=∑m1υi→j·yi+γj·g+bj(4)
其中υTj表示连接隐层和输出层节点j的权值向量,υi→j表示隐层节点i到输出层节点j的权值,bj表示对应偏置量,m为隐层节点数量,g表示特殊节点输入值,γj为对应权值。
3.2学习过程
整个训练过程基本采用BP算法的思想,首先,模型的整体MSE为:
![4HED[]DK@]6_G[QIV3}K]AV.png 4HED[]DK@]6_G[QIV3}K]AV.png](http://files.chinaaet.com/images/2017/04/07/6362716386612717967363517.png)
其中rj 为预测结果的实际值。为后续计算方便,这里添加了系数12。
训练学习过程以最小化MSE为目的,利用梯度下降算法,以目标负梯度方向对参数进行调整,对于误差函数(5)和给定学习率η,参数ωi→j的负梯度变化量为:
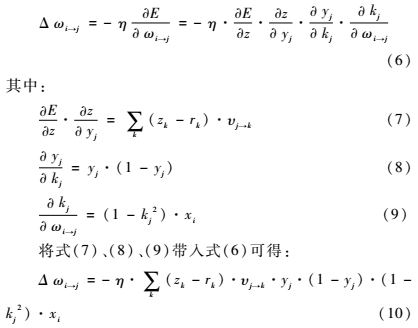
同理,根据式(10)同样的推导方式可以得到其他参数的变化量为:
![Y2U{`})$9J]}V~}~4QDJACE.png Y2U{`})$9J]}V~}~4QDJACE.png](http://files.chinaaet.com/images/2017/04/07/6362716388528499244792652.png)

4实验评估
本实验中的医疗数据源于国内某大型三甲医院的糖尿病患者的医疗数据。共有348位患者的信息,每个患者至少包括了3条以上的检查数据。共1 399条检查数据。数据以7:3的比例划分训练集和测试集。模型的输出为预测时间下的A1C、GLU、INS 3个指标的值。
4.1模型评价标准和参数设定

首先对模型的数值数据进行归一化处理。本节选取均方误差(Mean Square Error, MSE)和决定系数(coefficient of determination, R2)来作为实验的评价指标。两者的计算公式如下:
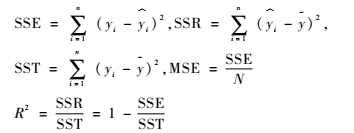
后续实验均选取R2来衡量实验结果。
图1给出了在不同BP迭代次数的情况下模型的R2值。可以看到,当BP的迭代次数大于500次时,模型预测结果的R2值已经基本保持不变。所以本文实验中对于每一次BP过程,每一个参数迭代500次或迭代至该参数收敛为止。

实验时模型采用动态学习率,学习率在每一个新样本进入模型时更新,学习率公式为:
![VV_J$V1]Q@7LF$~U72`K`2K.png VV_J$V1]Q@7LF$~U72`K`2K.png](http://files.chinaaet.com/images/2017/04/07/6362716390325520559174020.png)
其中,η′为上一个样本时模型的学习率。本系列实验中学习率的初始值为0.05。
4.2实验结果评估
在上述实验条件下,经过100次随机初值实验获得3个指标值预测结果的R2均值。实验可以看出,该模型对于本数据集的预测效果较好,无论是训练集还是测试集的决定系数R2都在0.6~0.8左右,模型的拟合程度较好。
实验过程中进行了对比实验,对比实验中使用了普通的BP神经网络、xgboost等算法对相同的数据进行了预测,在表4中可见各个算法的对指标预测的R2值。在对比实验结果中可以看到,本文提出的模型总体的表现最好; xgboost在测试集表现与本文提出的模型相近,但是迭代次数在20次时就已过拟合。而一般的神经网络模型拟合的效果较差,并不能达到良好的预测效果。
5结论
本文提出了一个基于BP神经网络,针对糖尿病医疗数据集所构建的改进神经网络预测模型。与一般的神经网络相比,该模型针对于特定数据集,添加了隐层用来保存上一次隐层节点的输出,修改了隐层的激励函数,加入了特殊节点来更好地拟合数据。在第四节的实验中,可以看到本文所构建的模型对于糖尿病的医疗数据集的预测有良好的表现。在预测准确性上,要优于传统的神经网络及其他的模型。
参考文献
[1] Cai Binghuang, Jiang X. A novel artificial neural network method for biomedical prediction based on matrix pseudo-inversion[J]. Journal of Biomedical Informatics, 2014, 48(3):114-121.
[2] PAPPADA S M, CAMERON B D, ROSMAN P M, et al. Neural network based real time prediction of glucose in patients with insulin-dependent diabetes[J]. Diabetes Technology & Therapeutics, 2011, 13(2):13541.
[3] WYSOCKI, LAWRYN'CZUK A, MACIEJ. Elman neural network for modeling and predictive control of delayed dynamic systems[J]. Archives of Control Sciences, 2016, 26(1):117 142.
[4] RODRIGUEZ P, WILES J, ELMAN J L. A recurrent neural network that learns to count[J]. Connection Science, 1999, 11(1):540.

