徐韦佳，田俊杰，施琴

　　（中国人民解放军理工大学 理学院，江苏 南京 211101）

       摘要：为了实现逐次逼近型模数转换器(Successive Approximation AnalogtoDigital Converter, SAR ADC)，在MATLAB平台上使用Simulink 工具，建立SAR ADC的理想模型，主要包括数模转换器（DAC）、比较器、译码器和寄存器模块。理论分析时钟抖动、开关非线性、比较器失调、电容失配等非理想因素对系统性能的影响，在理想模型基础上添加非理想因素，进行MATLAB仿真，通过分析输出信号频谱的变化，总结降低非理想因素对系统性能影响的方法，对实际电路设计具有指导意义。

　　关键词：SAR ADC；MATLAB；非理想因素

　　中图分类号：TN432文献标识码：ADOI： 10.19358/j.issn.1674-7720.2017.08.007

　　引用格式：徐韦佳，田俊杰，施琴.SAR ADC的系统级建模与仿真［J］.微型机与应用，2017,36（8）：19-22,25.

0引言

　　模数转换器(AnalogtoDigital Converter, ADC)作为连接外界模拟信号和数字信号处理系统的桥梁，得到了广泛应用。在诸多不同结构的ADC中，逐次逼近型ADC(SAR ADC)具有中等精度、尺寸小、功耗低、成本低等优点，广泛应用在工业控制、消费电子、信号采集等场合。近年来，随着CMOS工艺特征尺寸的不断减小，SAR ADC的速度跟精度不断提高，功耗跟电源电压不断降低，如何从系统级设计角度减小各种非理想因素对SAR ADC性能的影响，优化SAR ADC的架构设计，已成为当前研究热点之一。

　　当前SAR ADC的发展趋势是高速、高精度和低功耗。然而，由于一些非理想因素的存在，会影响SAR ADC系统的性能。当SAR ADC趋于高速的时候，任何微小的时钟抖动都会影响模数转换的精度。电源电压不稳定会造成系统性能的不稳定。开关非线性、器件失配、比较器失调、噪声等会造成系统精度的下降和功耗的增加，这些都是影响SAR ADC系统性能的非理想因素。因此，要设计出高性能的SAR ADC，总结降低非理想因素对系统影响的方法，尤为关键。

　　当前国内有关SAR ADC的研究大多着重于具体电路设计细节，而在系统级设计和建模等顶层设计方面的关注比较少［1］。今后ADC的发展趋势是片上系统(System on Chip, SOC)，这是一个集成了IP核、具有专用目标的集成电路，同时也是一项从确定系统功能开始，到软/硬件划分，最终完成设计的新技术。但是SoC也会带来新的噪声以及工艺相容性等新问题，这就需要设计者从系统级设计和建模中来验证后续电路设计的可行性和价值。

　　基于此，本文从系统级设计角度，使用Simulink工具构建理想模型，分析各种非理想因素对系统性能的影响，通过MATLAB工具仿真和对仿真结果的频谱分析，总结降低非理想因素影响的方法，得出在所能考虑到的因素范畴内的最优化架构设计。

1SAR ADC的工作原理和整体架构

　　图1是8位八选一多通道输入SAR ADC的电路结构示意图，包括多通道选择器、采样保持电路S/H和DAC组成的采样DAC网络、比较器、控制逻辑电路、移位寄存器和时钟电路。SAR ADC的工作原理基于二进制搜索算法。转换开始，在时钟信号作用下，首先控制逻辑电路将移位寄存器的上一级输出清零，并将最高位置1，输出结果D［0:7］被输入给采样DAC网络，转换为参考电压Vref，比较器将Vin和Vref进行比较，比较完成后，控制逻辑电路就将比较器的输出结果传递给移位寄存器，确定该位保持1还是清为0，同时将次高位置1，产生新的参考电压，进行下一位的模数转换。这样从高位到低位，如此循环，直到完成所有的比较，最后产生八位的数字编码输出［2］。

2SAR ADC的主要电路建模

　　2.18位DAC的理想模型

　　图2是8位DAC的MATLAB理想模型，使用二进制指数形式的信号放大增益表示二进制指数电容阵列，加法器用来实现电荷再分配功能［3］。时钟信号由SAR ADC的控制逻辑电路产生，控制DAC电容阵列的开关是连接地电位GND，还是连接采样电压Vin或是基准电压Vref。采样结束后，通过加法器，将各电容采集信号求和输出，这就是DAC的输出。

　　2.2比较器的理想模型

　　图3比较器的MATLAB理想模型图3是比较器的MATLAB理想模型，采样信号 Vin和 DAC 的输出 VDAC作为加法器的输入，求和的结果与高电平1和低电平0相比较，如果 Vin＞VDAC，则比较器输出VCOM为高电平1；如果 Vin＜VDAC，则VCOM为低电平1，实现了比较的功能［3 4］。

　　2.3控制逻辑电路的理想模型

　　以最高位D7和次高位D6的时序控制电路为例，图4是控制逻辑电路的MATLAB理想模型。对于最高位D7，当采样结束时采样时钟CLK处于低电平，最高位D7的置位信号到来，或者比较器的输出结果VCOM为高电平，会导致要转换的该位为高电平。此时逻辑控制电路控制DAC的最高位开关连接Vref，或者是维持该位的高电平。同样，对于次高位D6，采样结束时，CLK处于低电平，并且D7比较结束，置位信号恢复低电平，此时，如果D6的置位信号到来，或者该位的VCOM为高电平，最终的输出结果都是高电平，控制DAC的次高位开关接Vref，或者维持该位的高电平［3］。

　　8位SAR ADC的MATLAB系统理想模型包括采样保持电路、DAC、比较器、移位寄存器、输入模拟信号Vin、时钟信号CLK，输出为八位二进制数字编码［D7：D0］。

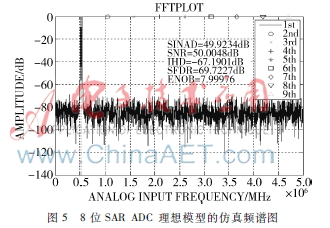
　　使用MATLAB仿真工具对该理想模型进行仿真［5］，仿真结果如图5所示。当采样时钟CLK频率为10 MS/s、输入信号频率约为0.5 MHz 时，取4 096个点进行FFT分析，仿真结果显示， ENOB=7.99 bit，SINAD=49.92 dB，SNR=50.00 dB，THD=-67.19 dB，SFDR=69.72 dB，说明该理想模型性能优良，能够实现模数转换功能。

　　3SAR ADC的非理想因素分析

　　SAR ADC的结构主要包括控制逻辑电路、DAC和比较器。其中，控制逻辑电路的非理想因素主要包括开关非线性和噪声，DAC的非理想因素主要包括电容阵列失配以及开关的非线性，比较器非理想因素主要是失调电压以及外接 CLK信号的时钟抖动造成的误差。下面将具体分析这些非理想因素对SAR ADC系统性能的影响。

　　3.1时钟抖动

　　时钟抖动效应指由于实际采样时刻的偏差，会导致采样结果产生误差。可以通过建模来确定系统能接受的时钟抖动的大小［6］。

　　设信号函数为f(t)，采样保持电路理想时刻采样值为f(nT)，实际采样值为f(nT+ΔT)，所以：

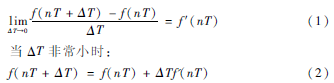
　　因此采样时钟抖动模型的设置如图6所示［7］。

　　3.2开关非线性

　　理想采样开关的导通电阻为0，断开时电阻无穷大。实际上，CMOS工艺下实现的MOS开关会出现时钟馈通和电荷注入等一系列非线性因素。假设Vin是输入，Vout是输出，栅压为高电平VDD时，MOS开关导通，则导通电阻Ron表示为［8］：

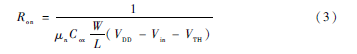
　　由公式（3）可知，开关的导通电阻Ron与输入信号Vin有关，是一个非线性函数，会限制输入电压范围。为了减小导通电阻Ron，可以采用大宽长比的晶体管，但是增大了面积，增大了寄生电容，从而影响开关速度［9］。

　　由于开关的非线性特点，一般采用 CMOS 传输门开关。CMOS传输门开关由 NMOS 管和 PMOS 管并联而成，总电阻相对稳定，变化范围小，弥补单个 MOS 管作为开关电阻值变化较大的缺陷，能够有效解决开关非线性的问题［10］。

　　3.3比较器的失调

　　比较器的失调电压主要包括静态失调和动态失调两部分［10］。静态失调指比较器对称的MOS管的迁移率μ、氧化层电容Cox和阈值电压Vth的不匹配带来的误差用下式表示：

　　其中，AμCox、Avth、SμCox、Svth是工艺参数，D是两匹配晶体管间距。所以，可以通过增加晶体管面积并且减小两管间距来减小比较器的静态失调。

　　动态失调指寄生电容失配而引起的误差。晶体管电容失配会导致充放电过程中电压值的变化，从而产生动态失调误差。可以通过增加晶体管面积来增加寄生电容，通过减小比值来减小比较器的动态失调误差。

　　3.4电容阵列的失配

　　DAC的电容阵列的失配会影响整个SAR ADC的系统精度。假设电容失配误差来自于单位电容C0的偏差，单位电容方差σ02，大小呈正态分布，每个输出对应的电容值为：

　　Ck=2n-kC0+δk,E［δk］=0,E［δ2k］=2n-kσ20（6）

　　由电荷再分配原理，给定数字码y，假设：

　　y=∑nk=12n－kBk（7）

　　计算可得，实际DAC与理想DAC的偏差，也就是DAC的INL为：

　　根据DNL的定义：

　　DNL(y)=|V(y)－V(y－1)－1LSB|

　　=|V(y)+Verr(y)－V(y－1)+Verr(y－1)－1LSB|

　　=ΔVerr(y)（9）

　　DNL方差为：

　　可以得出，电路的INL和DNL的方差与单位电容C0的平方成反比，与方差σ02成正比。因此可以通过增加C0来减小电容失配引起的误差。

　　对于电荷再分配式DAC，ADC位数为N，二进制加权电容网络允许的最大电容失配率δ满足：

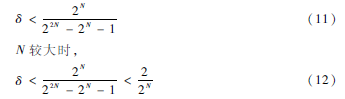
　　可以得出，随着精度N的增加，电容网络允许的最大电容失配率δ约成指数下降，当N很大时，电容网络失配误差与δ呈线性关系［11］。

4非理想因素仿真结果与分析

　　4.1时钟抖动仿真

　　图7是给SAR ADC理想模型加上采样时钟抖动后的系统仿真图。采样时钟CLK频率为10 MS/s，分别设置采样时钟抖动为0.1 ns，0.3 ns，0.5 ns，1 ns，进行FFT分析。仿真结果显示，时钟抖动为0.1 ns时，系统信噪比SNR为49.83 dB；时钟抖动为0.3 ns时，SNR为48.70 dB；时钟抖动为0.5 ns时，SNR为46.81 dB；时钟抖动为1 ns时，SNR为44.39 dB。说明采样时钟抖动会造成采样信号的偏差，从而降低系统SNR，进而降低系统的ENOB，因此为了降低抖动噪声的影响，采样时钟抖动应当控制在0.3 ns之内。

　　4.2比较器失调仿真

　　图8是给SAR ADC的理想模型加上比较器失调电压后的仿真图。采样率为10 MS/s，设置比较器失调电压为30 mV以内和50 mV以内。仿真结果显示，比较器的失调越大，有效位数越低。当失调为30 mV以内时，ENOB为7.94 bit；当失调为50 mV以内时，ENOB为7.56 bit，所以说，考虑到一定的余量，实际电路设计中，比较器的失调电压必须要控制在30 mV以内，否则会造成精度过低。

　　4.3电容失调仿真

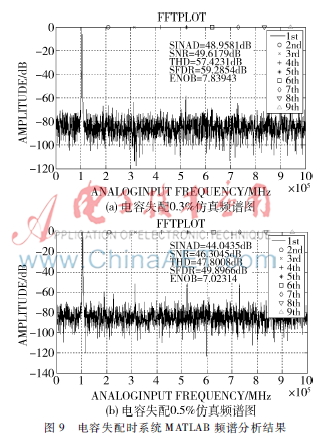
　　图9所示是DAC电容阵列失配的仿真频谱图。采样率为10 MS/s，设置电容失配率分别为0.3%，0.392 2%，0.5%，1%。FFT仿真结果显示，电容失配率为0.3%时，ENOB为7.83 bit；电容失配率为0.392 2%时，ENOB为7.61 bit；电容失配率为0.5%时，ENOB为7.02 bit；电容失配率为1%时，ENOB为5.61 bit。因此电容失配率越大，有效位数跟信噪比越差，系统性能变差。考虑到一定的余量，实际电路设计中，要控制电容失配率在0.5%以内。

5结论

　　本文从系统级角度，在MATLAB平台上使用Simulink 工具，对8位SAR ADC进行系统级建模，包括DAC二进制权电容阵列、比较器、控制逻辑电路和移位寄存器。在理想模型基础上，分析时钟抖动、开关非线性、比较器失调、电容阵列失配等非理想因素对系统性能的影响，总结降低非理想因素影响的方法。给理想模型添加非理想因素，进行系统的整体仿真。FFT仿真结果显示，要使SAR ADC实现较高的有效位数和信噪比，时钟抖动要控制在0.3 ns以内，比较器失调控制在30 mV以内，DAC电容失配控制在0.5%以内，不断优化系统架构设计，对实际电路设计具有指导意义。

参考文献

　　［1］ 张郭敏. 流水线ADC的系统建模与架构设计［D］. 合肥: 合肥工业大学, 2010.

　　［2］ 章大伟. 一种SAR ADC的设计与研究［D］. 合肥: 合肥工业大学, 2014.

　　［3］ 徐韦佳. 一种异步逐次逼近型模数转换器的研究与设计［D］. 合肥: 合肥工业大学, 2015.

　　［4］ 陈幼青, 何明华. 应用于14 bit SAR ADC的高精度比较器的设计［J］. 微电子学与计算机, 2011, 28(6): 109-112.

　　［5］ 刘旭东, 戴澜. 14位100 MHz流水线ADC行为级建模与仿真［J］. 微电子学, 2013, 45(5): 686689.

　　［6］ DEVRIM A, MOHAMMAD A S, FRANCO M. Switch boot strapping for precise sampling beyond supply voltage［J］. IEEE Journal of SolidState Circuits, 2006,41(8):1938- 1943.

　　［7］ 孙肖林, 吴毅强. 4bit FLASH ADC行为级建模与仿真［J］. 现代电子技术, 2013,36(22): 120-123.

　　［8］ 毕查德·拉扎维(美). 模拟CMOS集成电路设计［M］. 陈贵灿，程军，张瑞智，译.西安: 西安交通大学出版社, 2013.

　　［9］ ALLEN P E, HOLBERG D R. COMS analog circuit design, Second Edition［M］. 北京: 电子工业出版社, 2002.

　　［10］ 江向阳. 一种SigmaDelta调制器的研究与设计［D］. 合肥: 合肥工业大学, 2014.

　　［11］ 周文婷, 李章全. SAR A/D转换器中电容失配问题的分析［J］. 微电子学, 2007, 37(2): 199-203.