文献标识码: A
DOI:10.16157/j.issn.0258-7998.166011
中文引用格式: 吴衍,马碧芳,李立耀,等. 基于优化求导经验模式分解法的谐波检测方法[J].电子技术应用,2017,43(8):140-143.
英文引用格式: Wu Yan,Ma Bifang,Li Liyao,et al. A novel method of detecting harmonic currents used DEMD algorithm[J].Application of Electronic Technique,2017,43(8):140-143.
0 引言
谐波检测算法是有源电力滤波器(APF)的一个重要组成部分,算法的准确性和实时性在很大程度上决定了APF的性能,因此近10多年来国内外专家学者在这一领域投入了很大的研究精力,并取得了丰硕的成果,其中比较有代表性的算法包括基于瞬时无功功率理论的ip-iq法、基于神经网络的自适应检测法、小波变换检测法和经验模式分解(EMD)算法等[1-3]。但这些方法都各有不足,如ip-iq法需要三相同步测量,且检测精度和实时性过于依靠低通滤波器的性能,稳定性不高;自适应法需要大量的训练样本,过程繁杂;小波分析法算法构造复杂,检测过程需选取合适基函数,不能根据自身特点分析[4];EMD算法是近年来崛起的优秀检测算法,但存在端点效应问题,分解结果易造成污染,产生失真。上述诸法的准确性和实时性由于这些缺陷而大打折扣,在需要在线实时跟踪测量谐波的场合使用上捉襟见肘。因此,针对以上谐波检测法的缺点,提出一种新颖的谐波检测新方法。
1 优化求导经验模式分解(DEMD)算法
DEMD是在经验模式分解(EMD)算法的基础上改进的,既解决了EMD法的端点效应问题,又保留了EMD算法的重要特性,即它是基于信号自身性质的自适应信号分析法,它能有效地捕捉到信号中非线性和不稳定的谐波振荡,具有很强的实时性。DEMD算法的基本原理是对给定的信号序列X(t),将其按照筛分过程分解成内在模式函数(IMF),它实现的效果就是将含有基波分量、谐波分量和噪声干扰的电流信号精确分解成各信号分量。DEMD算法的步骤如下:

(2)通过获得实际信号数据X(ti)与上下包络线平均值m(ti)的差,得到理论上的IMF分量h(ti),即hj(ti)=X(ti)-mj(ti)。
(3)为了保证IMF分量在振幅和频率上有物理意义,还需要将hj(ti)进行进一步的筛分直到符合要求。令X(ti)=hj(ti),重复步骤(1)和(2),设定筛分过程的停止准则,使用参数标准偏差SD,它的算式如下:

本文中当筛分过程中的SD<0.2时,得到的hk(ti)满足IMF分量的条件,才是一个符合要求的IMF分量。

由式(4)可知此法能很好地实现电流信号基波和谐波分量的分离,cm(ti)为基波IMF分量,c1(ti)+c2(ti)+…+cm-1(ti)为谐波IMF分量之和,rm(ti)为余量,即趋势分量[5-8]。
2 端点效应问题的处理策略
端点效应是影响EMD法准确性的重要因素之一,端点效应造成的误差会向信号序列内部扩展开,以致污染IMF分量使其产生失真。
由于在非端点处的二阶导数在其局部极值点上是连续的,而在两个端点处的局部极值(e(t1)、e(tN))和其一阶导数(e′(t1)、e′(tN))都是未知的,因此无法满足紧致差分公式的,这是端点效应现象的最大问题。为了克服这个问题,提出一种利用埃尔米特多项式来求上下包络线的方法,处理方法如下:

根据二次导数的连续性,在第一个端点t1处,对(t1-0)使用二次样条插值(式(5))和(t1+0)使用三次样条插值(式(1))得出:

这样端点的一阶导数qL和qR的值就能被求得,上下包络线也可以很好的确定,在电力系统工程中此策略效果很好,解决了端点效应问题,所产生误差在可以接受的范围内[9]。
3 谐波检测系统设计
采用美国德州(TI)公司DSP处理器TMS320F28335做为处理运算核心来设计谐波检测系统,主要完成数据的AD转换、谐波检测算法、控制算法和上位机交互显示等功能。所设计的谐波检测系统电路结构框图见图1。
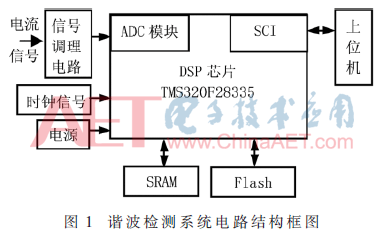
该系统采用信号调理电路将被测信号和DSP处理器相隔离,并将待测电压转换成0~3 V采样信号。DSP处理器TMS320F28335使用16通道12位ADC模块实现信号的高速采集转换,然后将采样处理后的信号进行DEMD法运算,获得各次谐波和基波IMF分量,并且运用希尔伯特(Hilbert)变换获得数据的时频分析结果。使用SCI接口与上位机通信,将结果上传至上位机,在上位机中分析处理数据,生成文件、报表和曲线,并在屏幕上显示。
4 仿真与实验
4.1 准确度和有效性仿真试验
为了验证DEMD算法不仅能准确有效地分解电流信号,同时可以很好地抑制端点效应问题,设计了检测电力系统谐波电流的实验电路。假设被检测对象为一相电流,直流侧接有阻感负载。采用DSP TMS320F28335实现DEMD算法,对其进行仿真实验,实验结果在上位机中显示。设电力系统电流仿真信号i(t)为:

实验分解结果如图2所示。由图2中可以清楚地看到该检测法可以将电流信号准确地分解成各个频率信号分量,且这些分量在时域分布中均为连续,图1中电流基波分量iC4及电流谐波分量iC1、iC2、iC3和余量ir都直观地反映出电源电流信号i被分解的变化规律,其中余量ir与原始信号中的趋势分量相对应。

为了验证DEMD算法很好地抑制了端点效应问题,从图2(f)中测量出余量ir的变化范围为0到0.212 4,并计算其与原信号中趋势分量的相关系数(CORR)的值为0.998,相对均方根误差(RRMSE)的值为0.019 1,从这些数值可以看出DEMD算法以高相关性、低相对均方根误差性在确定端点处包络线和确定信号趋势走向的准确度上有着优越的表现,同时很好地抑制了端点效应问题,这些都表明了DEMD法确实能准确、有效地提取电流信号的基波和谐波分量。
4.2 实时性仿真试验
为验证DEMD算法满足谐波检测的实时性要求,设计了一种动态谐波检测的仿真实验:设输入电流信号i为50 Hz基波频率的非平稳非线性负载电流,含有3、5、7、9次谐波,仿真时间为0.12 s,在0.04 s处将电流信号突变(呈现非平稳状态),幅值增大为原来两倍,以此来检验DEMD算法跟踪谐波电流的能力,实验仿真结果如图3所示。与文献[10]改进型ip-iq法相比(该法在谐波电流突变3/4个周期后才跟踪上基波的检测,即延时约为0.015 s),图3(b)、(c)中检测非平稳非线性电流i的实时性良好:当信号i在第3个周期幅值开始突变时,图3(b)中可见,新方法快速地跟踪基波,延时仅约为4 μs,并且检测出i的基波分量if和谐波分量ih与文献[10]中对应的波形相同。将此结果导至ORIGIN软件分析可知,DEMD算法检测基波幅值与期望幅值之误差仅为1.01%。可见新方法在信号非线性和非平稳时都能跟踪谐波、较准确地检测出基波和谐波分量[10]。

5 结论
本文采用DEMD算法设计了谐波检测器,这一全新算法很好地抑制了端点效应问题,可以有效地分解出电流信号的基波和谐波分量。仿真实验结果表明DEMD法可以准确有效地实时、跟踪检测非线性和非平稳电流信号,对端点效应问题产生的误差污染IMF分量现象有了明显的抑制。新方法特别适合于APF的电流跟踪控制电路,用来对电力系统有畸变、非平稳非线性谐波电流信号实施快速实时检测。
参考文献
[1] 王兆安,杨君,刘进军.谐波抑制和无功功率补偿[M].北京:机械工业出版社,2002.
[2] 成立,吴衍,王鹏程,等.运用因散经验模式分解算法的谐波检测新方法[J].江苏大学学报:自然科学版,2010,31(06):687-690.
[3] 成立,范木宏,王振宇,等.基于瞬时无功功率的改进型谐波电流检测法[J].高电压技术,2007,33(4):46-49.
[4] 付巍,吴忠燕,朱岩,等.基于希尔伯特-黄变换的飞机供电系统谐波信号分析[J].电测与仪表,2011,48(06):14-18.
[5] Zhang Xu,Zhou Ping.Filtering of surface EMG using ensemble empirical mode decomposition[J].Medical Engineering & Physics,2013,35:537-542.
[6] Majid Norouzi Keshtan,Mehrdad Nouri Khajavi.Bearings fault diagnosis using vibrational signal analysis by EMD method[J].Research in Nondestructive Evaluation,2016,27(3):155-174.
[7] Valentina Bono,Saptarshi Das,Wasifa Jamal,et al.Hybrid wavelet and EMD/ICA approach for artifact suppression in pervasive EEG[J].IEEE Journal of Neuroscience Methods,2016,267:89-107.
[8] Kais Khaldi,Bruno Torresani.HHT-based audio coding[J].ORIGINAL PAPER,2015(9):107-115.
[9] CHUA P C,FAN C,HUANG N. Derivative-optimized empirical mode decomposition for the Hilbert-Huang transform[J].Journal of Computational and Applied Mathematics,2014,259:57-64.
[10] 居茜,鞠勇.一种改进的单相电路ip-iq谐波检测方法[J].南京师范大学学报:工程技术版,2014(2):24-29.
作者信息:
吴 衍,马碧芳,李立耀,陈国钦
(福建师范大学福清分校 电子与信息工程学院,福建 福清350300)

