0 引言

    随着越来越多的商业无人机厂商的兴起，四旋翼如今已经走进了人们的日常生活，在社会生活的很多方面都发挥了重要作用，比如航拍、农业、交通检测、抢险救灾、地形勘测等领域。四旋翼作为一个研究平台，在科研领域也获得了广泛的应用^[1-3]，一些研究者将一些先进的控制技术应用于四旋翼的飞行控制中，还有一些研究者着眼于使无人机更智能化，研究了无人机的视觉导航^[4]、智能飞行等。

    姿态解算对于四旋翼的控制有着非常重要的作用。要使飞机能在空中平稳的飞行，精确的姿态解算不可或缺。常见的姿态解算算法有互补滤波、卡尔曼滤波以及扩展卡尔曼滤波等。EKF虽然计算复杂，但精度高，也受到了越来越多人的青睐。本文首先推导了四旋翼的数学模型；之后提出了微机电传感器的线性数学模型，并对传感器进行了仿真；介绍了扩展卡尔曼滤波器的设计过程，并在MATLAB仿真模型中验证了滤波的效果；最后在实际飞机上进行了验证。

1 四旋翼的数学模型

    四旋翼飞行器可以在机体坐标系和惯性坐标系下分别建立其动力学模型^[5]。通常在机体坐标系中建立它的动力学方程,最主要的原因是传感器所测量的值就是相对于机体坐标系的，所以自然而然要在机体坐标系中建立方程。

    在建立物理模型之前，需要建立两个不同的笛卡尔参考坐标系——惯性坐标系和机体坐标系。本文采用欧拉角的方式描述四旋翼的姿态。姿态角就是用来描述两个坐标系的位置关系。

1.1 姿态角的描述

    欧拉角是一种描述刚体相对于一个给定参考坐标系位置的方式。按照惯例采用的旋转顺序是z-y-x，相对应的角度分别为yaw、pitch、roll。3个基本旋转矩阵的乘积就是两个坐标系之间的转换矩阵，如式(1)所示^[6]。

1.2 动力学方程

    对于四旋翼飞行器，在机体坐标系下，使用牛顿-欧拉公式^[7]可得到刚体质心的动力学矩阵表达形式：

    四旋翼飞行器为欠驱动系统，控制输入量只有4个，即4个旋翼的转速。本文选取的4个变量为3个姿态角（横滚角、俯仰角、偏航角）和飞行高度。还要选择合适的控制变量，使得动力学方程相对于控制变量是线性的。                                             

    根据式(2)，可以得到四旋翼在机体坐标下的数学模型^[7]：

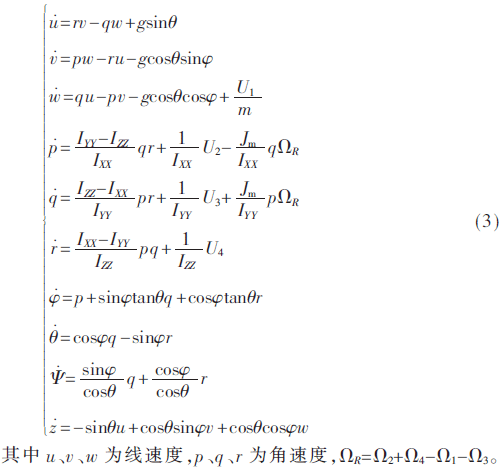
2 传感器模型

    四旋翼上的传感器为导航和姿态控制系统提供信息。目前传感器都采用的是微机电系统（MEMS）技术，通常把飞机上的传感器合称为惯性导航单元（IMU）。IMU主要有以下几部分组成：加速度计、陀螺仪、磁力计。

    一个典型的三轴微机电传感器的线性模型^[8]为：

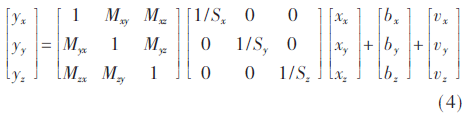
其中，x_i为各轴的输入值，y_i为输出值，b_i为在各轴上的偏差，v_i为在轴上的高斯噪声分布，S_i为标量因子，M_ij为轴与轴之间的敏感度。

    式(4)是一个对MEMS传感器建模的一般公式，即陀螺仪、加速度计、磁力计以及气压计都可以用这个公式来表示。下文在MATLAB仿真建模时，就是根据上面的数学模型设计的。

    完整的测量方程组如式(5)所示，y_a、y_g、y_m分别表示加速度计、陀螺仪和磁力计的输出。

3 EKF姿态解算

    应用标准卡尔曼滤波器的一个主要的限制是，它要求动力学方程和测量方程相对于状态变量来说都是线性的。但是在实际应用中这样的要求通常是不满足的，所以应用标准卡尔曼滤波受到了很大的限制。而扩展卡尔曼滤波就是为了克服标准卡尔曼滤波器的这个缺点而提出的，它能适用于当系统和测量模型是非线性的情况^[9-12]。

    EKF进行线性化的操作是通过计算状态矩阵和测量矩阵的雅克比矩阵来进行的。针对连续EKF，定义雅克比矩阵的式子为：

    根据方程组(3)，可计算它们的雅克比矩阵。

    对测量方程进行线性化，得到一个10×10的稀疏矩阵：

其中，J₁为加速度传感器方程相对于线速度u、v、w的偏导数，J₂为加速度传感器方程相对于角速度p、q、r的偏导数，J₃为磁力计相对于欧拉角的偏导数，J_a为标量是对高度变量的偏导数。计算的表达式如方程组(9)所示。

    同理，对状态方程进行线性化，结果也为一个10×10的稀疏矩阵，具体计算的各项在这里就不一一列出。

    上面就是通过雅克比矩阵线性化后的状态转移矩阵和测量矩阵，可将新的F和H代入卡尔曼滤波的方程组中。

    EKF的数学描述就是在当前时刻估计的状态上，采用泰勒级数展开，并且去掉高阶项，基本上只取一阶的泰勒式子。线性化的方式就是针对转移矩阵和测量矩阵，计算它们的雅克比矩阵。所以它的计算量比标准卡尔曼滤波大很多，因为它要实时更新和计算状态转移矩阵和测量矩阵。

4 仿真实验

    根据上面所建立的四旋翼、传感器和EKF的数学模型，在MATLAB上用Simulink搭建其模型。

    所搭建的整体仿真模型如图1所示，由输入信号、PID控制器、四旋翼仿真模型、传感器仿真模块（On-board IMU）、EKF滤波器模块、状态显示等模块组成。根据实验室所搭建的无人机，进行相应的估计，选择近似的参数，一些主要参数：m=1.023 kg，I_xx=I_yy=9×10^-3，I_zz=1.8×10^-2，J_m=3.4×10^-5，L=18 cm。

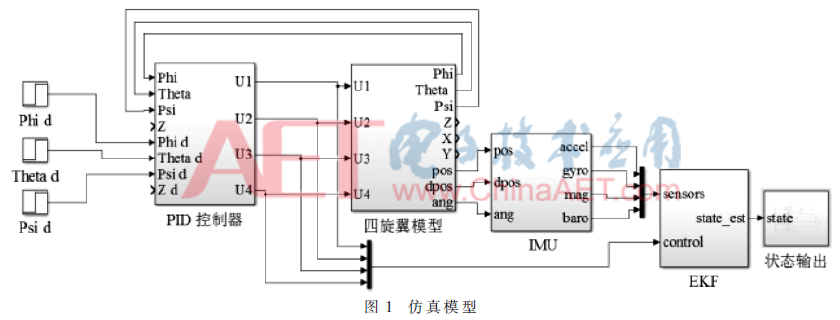
    当四旋翼处于悬停时，即给定的3个欧拉角为0，则经过传感器仿真模块on-board IMU后，得到的传感器的模拟图像为图2所示，因为传感器各轴的数据处理方式相同，所以这里只给出了加速度计X轴的仿真图。

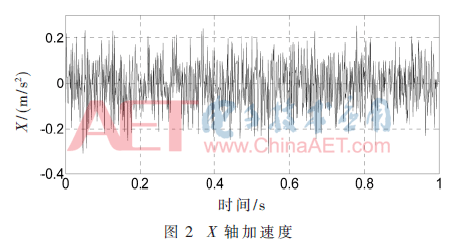
    经过扩展卡尔曼滤波后，可以从中解算出方程中的状态变量，仿真结果如图3～图5所示。

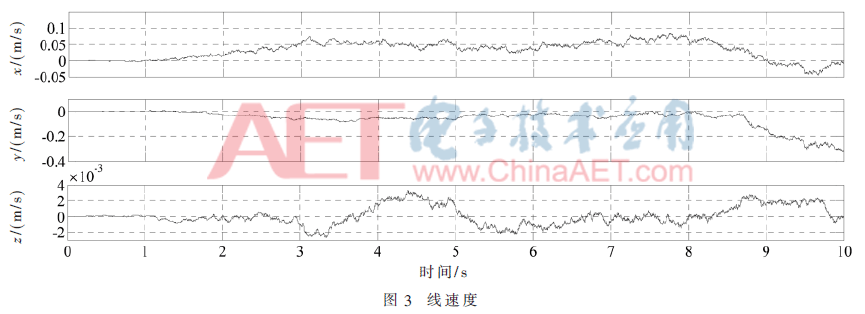
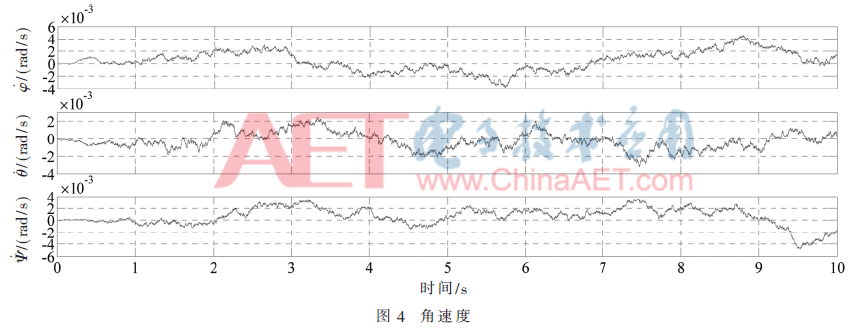
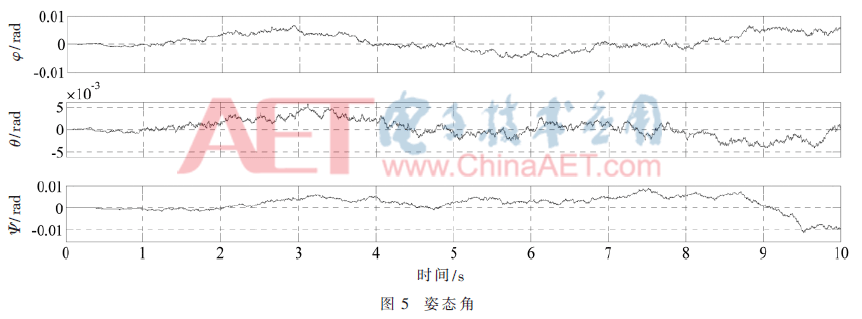
    由图像可知，信号经过传感器仿真模块后，信号变“差”了，这正是本设计模拟实际传感器希望达到的效果，这种信号更贴近实际四旋翼采集的传感器信号，只不过这里的噪声是人为添加的。当这种有着噪声的信号经过EKF滤波后，信号相对来说变得干净了，且能反映出信号变化的大体趋势，并且稳定在期望值附近，误差也较小，表明扩展卡尔曼滤波确实起到了效果，能滤除噪声，解算出正确的姿态角。

    在实验室搭建的无人机^[13]上进行了EKF滤波实验，测试无人机在悬停时的滤波效果。

    图6～图8记录了无人机在悬停时解算出的线速度，可以看出各轴线速度值比较稳定，在0值附近上下小幅度浮动。

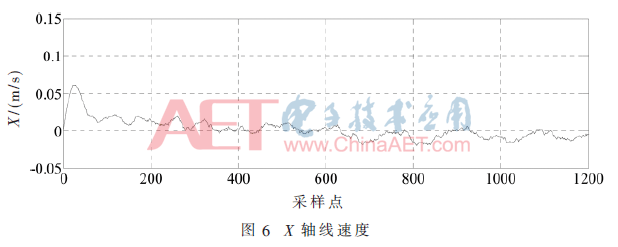
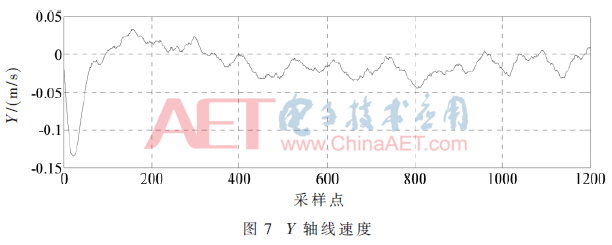
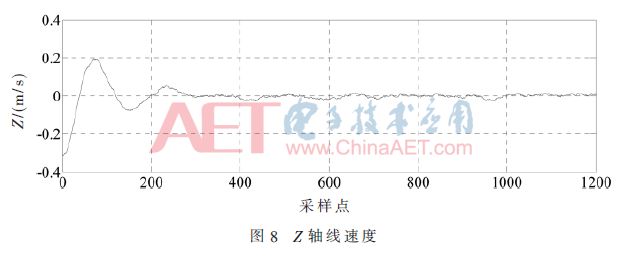
5 结论

    本文根据传感器和EKF的数学模型，在MATLAB搭建了它们的仿真模型，对传感器和扩展卡尔曼滤波进行了仿真验证。仿真实验是假设四旋翼在悬停状态下，即3个欧拉角都为0。经过传感器模块后，发现本来是很光滑的信号变成了有很多毛刺的信号。因为根据传感器的数学模型，在仿真模块中加入了延迟、偏差、标定因子、各个轴之间的影响因子等变量，所以信号就变得不光滑了。然后将信号送入到EKF模块，并结合四旋翼的控制量，解算出在机体坐标系下的状态变量。从仿真结果可以看出，解算出来的状态变量变得较为平滑，且大体上都在0附近，符合预期的值，说明EKF滤波起到了效果。最后也在实际的无人机上进行了验证。

参考文献

[1] Li Yibo，Song Shuxi.A survey of control algorithms for quadrotor unmanned helicopter[C].2012 IEEE fifth International Conference on Advanced Computational Intelligence(ICACI).Nanjin，Jiangsu，China：IEEE，2012：365-369.

[2] Zhang Xiaodong，Li Xiaoli，Wang Kang.A survey of modelling and identification of quadrotor robot[C].Abstractand Applied Analysis，2014.

[3] 蔡伟平，胡越黎，杨文荣，等.四旋翼双环滑模姿态控制系统设计与仿真[J].电子技术应用，2015，41(7)：150-153.

[4] MEIER L，TANSKANEN P，HENG L.PIXHAWK：A micro aerial vehicle design for autonomous flight using onboard computer vision[J].Autonomous Robots，2012，33(1)：21-39.

[5] MAHONY R，KUMAR V，CORKE P.Modeling，estimation，and control of quadrotor[J].IEEE Robotics & Automation，2012，19(3)：20-32.

[6] 秦永元.惯性导航(第2版)[M].北京：科学出版社，2014.

[7] BOUABDALLAH S.Design and control of quadrotors with application to autonomous flying[D].Lausanne:Lausanne Polytechnic University，2007.

[8] ASCORTI L.An application of the extended Kalman filter to the attitude control of a quadrotor[D].Milano：Politecnico Di Milano，2013.

[9] 邹波，张华，姜军.多传感器融合的改进扩展卡尔曼滤波定姿[J].计算机应用研究，2014，31(4)：1035-1038.

[10] 刘洪剑，王耀南，谭建豪，等.基于加速度变噪声EKF的无人机姿态融合算法[J].2016，30(3)：333-341.

[11] TARHAN M，ALTUG E.EKF based attitude estimation and stabilization of a quadrotor UAV using vanishing points in catadioptric images[J].Journal of Intelligent & Robotic Systems，2011，62(3)：587-607.

[12] MUNGUIA R F，GRAU A.A practical method for implementing an attitude and heading reference system[J].International journal of advanced robotic systems，2014，11(1)：1-12.

[13] 黄建，胡越黎，杨文荣，等.组合导航系统在四旋翼无人机上的实现[J].电子技术应用，2015，41(5)：167-170.

作者信息：

金舒灿1，2，胡越黎1，2，3，张  贺1，2

（1.上海大学 机电工程与自动化学院，上海200072；2.上海市电站自动化技术重点实验室，上海200072；

3.上海大学 微电子研究与开发中心，上海200072）