文献标识码: A
DOI:10.16157/j.issn.0258-7998.170338
中文引用格式: 张翕茜,李凤莲,张雪英,等. 基于代价敏感混合分裂策略的多决策树算法[J].电子技术应用,2017,43(10):128-131,136.
英文引用格式: Zhang Xiqian,Li Fenglian,Zhang Xueying,et al. A multiple decision tree algorithm based on cost-sensitive hybrid splitting strategy[J].Application of Electronic Technique,2017,43(10):128-131,136.
0 引言
瓦斯突出一直高居所有矿井事故之首。如果能在事故发生之前进行有效瓦斯突出预测,对降低矿井瓦斯事故发生、提高煤矿安全生产效率,具有非常重要的意义。分类算法可以通过抽取历史数据的重要信息以预测未来数据的发展。在煤矿瓦斯预测中,决策树算法因为模型简单,便于实时计算,可以处理离散型和连续型数据,且结果易于理解等特点,常被用于瓦斯预测模型构建。
决策树算法的研究主要分为两类:(1)对单决策树算法的改进,例如C4.5、CART、SPRINT和SLIQ[1];(2)使用集成分类器,提高准确性,例如:Bagging、Boosting和随机森林(Random forests,RF)。其中,随机森林属于广泛应用的较好的集成分类器[2],可以解决单决策树过拟合的分类准确性低下问题。本文的研究是基于随机森林的改进。
分类器对一种类别的过多训练会导致另一类分类准确度降低,从而使分类器易过拟合导致少数类准确度降低。在煤矿瓦斯预警中的具体体现是:瓦斯突出或危险状况下的数据稀少,为少数类,安全状态下的数据占多数,为多数类,导致分类器对少数类预测准确率偏低,从而造成对可能发生瓦斯突出隐患的漏报现象。
面对不平衡数据分类问题,传统决策树算法缺陷是对少数类学习不充分,易造成分类结果偏向多数类现象[3],使得表现为危险的异常情况,其预测准确率反而大大降低[4]。针对此问题,国内外研究方法主要有两方面:(1)改变数据分布结构,利用过采样和欠采样的手段,使数据分布易于算法执行和处理[5-6],但是此方法容易造成多数类信息缺失或少数类学习不充分;(2)对分类器进行改进,改进分类评价指标,使分类器能够较准确地处理不平衡数据[7-8]。在针对分类器的改进中,目前最流行的方法是加入代价敏感因子[9],其实现机理是对少数类分类错误给予一个较大权重的惩罚代价因子,同时对多数类分类错误给予一个较小权重的惩罚代价因子。例如,文献[10]提出了一种代价敏感随机森林算法,在随机森林的基础上加入代价敏感因子,以提高在不平衡数据问题上对少数类的预测。然而在随机产生决策树过程中,因为少数类数据的训练样本少和属性选择不全的原因,依然存在只有个别决策树对少数类得到充分训练,进而导致结果偏向多数类的预测缺陷。
本文针对不平衡数据集特点,提出了一种基于混合属性的代价敏感多决策树算法,算法首先将Gini指标和信息增益指标线性组合作为属性选择策略,进而用代价敏感因子对组合策略进行加权,最后使用输入样本的每个属性作为多决策树的根节点,改进代价敏感随机森林算法只采用部分属性作为根属性选择方式缺陷,达到保证多数类分类准确性的前提下,有效提高少数类分类准确性的目的。
1 混合分裂属性指标的确定
决策树构建的准确度主要取决于分裂属性的选择策略,本文采用组合策略是在结合C4.5和CART算法的基础上,融合代价敏感因子形成的分裂属性。其属性选择策略AS(Attribute Selection)如下:

式中,Ginisplit(A)(T)表示属性A划分后的Gini指数,是CART算法的分裂指标;GainRatio表示属性A划分后的信息增益率,是C4.5算法的分裂指标;C(Aj)表示集合T经过属性Aj分裂后的误分代价。
定义1:误分代价:对于二分类问题,给定一个样本集S,其含有s个样本,Aj(j=1,2,…,n)个属性。每个属性Aj含有m个取值ai(i=1,2,…,m)。那么属性Aj分裂后的所有子集总的误分代价可以表示为:

式中,P(i)是分裂后样本数量占分裂前的总概率,C(i)表示属性值ai的样本子集所构成的总代价[11]。
2 代价敏感混合属性多决策树算法
随机森林的每棵决策树的训练样本是随机抽取的,在不平衡数据集中,少数类被抽取到的概率几乎为零,因此在最后决策树形成过程中,少数类不会得到充分训练,结果会偏向多数类。
传统的决策树分类算法在构建决策树过程中,通过对每个属性的分裂点进行决策计算,分裂点的选择容易受属性个数和训练样本大小的影响。这种选取方法并未考虑根节点对决策树构建的影响,及其对预测结果的影响;尤其在不平衡数据分类问题中,对少数类的错误影响会造成致命后果。如果根节点选择错误,那么在后续分裂过程中想要纠正决策树代价非常巨大。
本文提出了代价敏感混合属性多决策树算法 (Cost-sensitive Hybrid Measure Attributes Selection Multi-Decision Tree,CHMDT),该算法原理框图如图1所示,其中采用每个属性作为根节点分别建树,即建树过程使用了全部属性。目的是训练过程中保证所有少数类和属性得到充分学习。
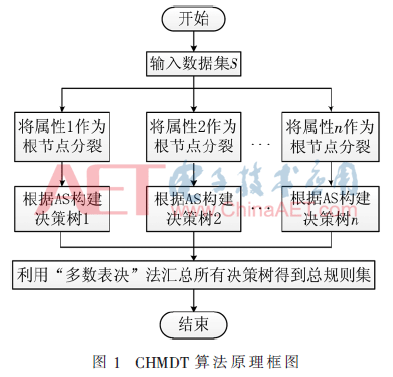
2.1 CHMDT算法流程
CHMDT采用广度优先的算法设计,即先采用所有属性作为各树的根节点进行分裂,然后每个根节点依据混合策略分裂属性为依据单独建树,具体实现流程如下:
输入:训练样本集S
输出:一个多决策树
Make Multi-Decision Tree(S){
If(S满足终止条件) Then return;
For(i=1;i<样本中属性个数;i++)
以第i个属性作为根节点分裂;
For(j=1;j<样本中剩余属性个数;j++)
根据式(1)计算各属性分裂点的混合分裂属性指标;
找出最佳分裂点,将S分为SL和SR;
Make Decision Tree(SL);
Make Decision Tree(SR);
返回训练规则集;
汇总规则集;
}
2.2 混合属性单决策树算法流程
CHMDT在根节点选择确定之后分别采用代价敏感混合策略属性单决策树算法(Cost-sensitive Hybrid Measure Decision Tree,CHDT)建树,采用式(1)的分裂指标。算法流程如下:
Make Decision Tree(S){
If(S满足终止条件) Then return;
For(i=1;i<S中属性个数;i++)
计算各属性分裂点的混合分裂属性指数;
找出最佳分裂点,将S分为SL和SR;
Make Decision Tree(SL);
Make Decision Tree(SR);
}
其中,SL代表S的左分枝,SR代表S的右分枝。决策树最终是一棵二叉树。
算法的终止条件为以下任一个条件满足:(1)S中的训练样本都为同一类别,即决策树达到叶子节点;(2)S中训练样本数达到某一阈值;(3)属性全部分裂完毕,没有待分裂属性。
3 实验及分析
本实验目的主要是验证代价敏感混合属性分裂指标在少数类分类和整体准确率预测性能的优势,以及提高所提出的CHMDT性能。
3.1 实验数据
实验数据集采用UCI和KEEL-Imbalanced Data Sets中的11个不同平衡率的非平衡数据集,详情如表1所示。

3.2 实验设置
训练样本与测试样本比为2:1,保证类别比重不变。为避免偶然因素,每个测试集进行10次交叉验证实验,每次实验训练样本和测试样本都打乱顺序随机分配。实验分为两种场景进行验证。
(1)场景一(验证代价敏感混合属性性能好坏):CLDT与CART、C4.5、ID3对比。
(2)场景二(验证CLMDT性能好坏):CLMDT与RF、代价敏感混合属性随机森林(CH-RF)对比。
3.3 评价指标
本文采用真实正类率和准确率作为评价指标,其中实验指标类别信息定义如表2。

(1)真实正类率TPrate/负类率TNrate:正确预测的正类/负类与实际为正类/负类的样本数量的比值(取值范围为0~1)。其值越大说明正类/负类预测越准确,性能越好。
真实正类率:
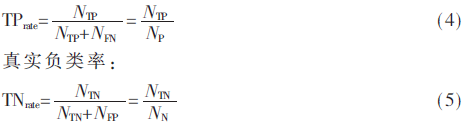
(2)准确率:正确预测的样本数与总样本数的比值(取值范围为0~1)。其值越大说明总体预测越准确,性能越好。

3.4 实验结果
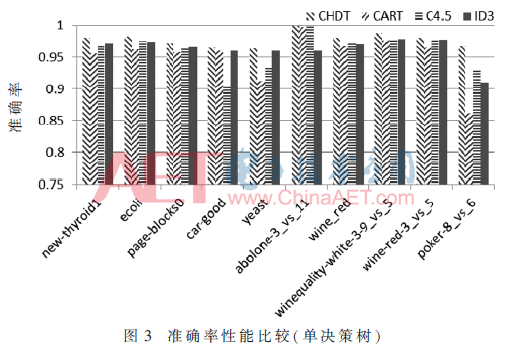
场景一: CHDT算法与其他单决策树算法在真实正类率预测性能比较如图2所示。具体分析实验结果可知,对数据ecoli、car-good、wine-red4、poker-8_vs_6,CHDT算法较ID3分别提升8%、11%、9%、8%。总体准确率比较如图3所示,可以看出,CHDT一直保持稳定且较高的准确率。

场景二:CHMDT算法与RF、CH-RF算法在真实正类率预测性能比较如图4所示。对数据集new-thyroid1、ecoli、page-blocks0来说,CHMDT算法相比其他两种方法有一定的增长;对数据集yeast、abolone-3_vs_11来说,CHMDT算法相比其他两种方法有较大提升;剩余数据集中,因为少数类样本较少,RF和CH-RF出现“一边倒”现象,少数类预测为0,但CHMDT算法均得到了一定的真实正类率预测结果。总体准确率比较如图5所示,可以看出,CHMDT算法较其他算法准确率都略有提高。


3.5 结果分析
从场景一的实验结果来看,采用CHDT算法在保证较高真实正类率预测结果的同时,准确率依然保持较高。从场景二的实验结果来看,RF算法在少数类训练样本极少的情况下,预测结果会偏向多数类,CH-RF算法有适当提升。总的来说,CHMDT算法在少数类样本稀缺的情况下有良好的少数类预测性能和较高的整体预测准确性。
4 煤矿瓦斯预警有效性验证
本实验选取同一工作面、不同时刻的煤矿瓦斯监测数据共461条,其中瓦斯突出数据26条,安全数据435条。属性值分别来自井下16个不同测点的传感器数据发回。CHDT算法与C4.5、ID3及CART预测性能比较如图6所示,可以看出,CHDT算法对正类的预测正确率提高的同时,负类率及准确率性能依然保持。多决策树算法预测性能比较如图7所示,可以看出,与RF及CH-RF算法相比,本文提出的CHMDT算法对正类样本的预测性能有明显提高,有效避免了因随机选择属性导致的属性信息丢失和少数类欠训练问题,同时负类率及准确率性能没有受到影响。


5 结束语
本文基于C4.5和CART算法的分裂属性用于非平衡数据集时少数类预测性能不佳的缺陷,提出了融合代价敏感指标的混合策略分裂属性,并将其作为随机森林算法属性选择措施,得到了基于代价敏感混合策略分裂属性的多决策树算法CHMDT。实验结果表明,该方法有良好的少数类预测性能和较高的整体预测准确性。将该方法用于煤矿瓦斯预警数据中,实验结果表明,本文所提出的方法可有效提高煤矿瓦斯预警数据整体预测性能。但采用所有属性作为根节点信息,在属性信息较多时,会存在算法复杂度偏高的问题,为此,下一步将继续研究基于分布式存储架构的多决策树实现方式。
参考文献
[1] KOTSIANTIS S B.Decision trees:a recent overview[J].Artificial Intelligence Review,2013,39(4):261-283.
[2] BANFIELD R E,HALL L O,BOWYER K W,et al.A comparison of decision tree ensemble creation techniques[J].IEEE Transactions on Pattern Analysis & Machine Intelligence,2007,29(1):173-80.
[3] XUE J H,HALL P.Why does rebalancing class-unbalanced data improve AUC for Linear discriminant analysis?[J].Pattern Analysis & Machine Intelligence IEEE Transactions on,2015,37(5):1109-1112.
[4] 杜春蕾,张雪英,李凤莲,等.改进的CART算法在煤层底板突水预测中的应用[J].工矿自动化,2014,40(12):52-56.
[5] VARLAMIS I.Evolutionary data sampling for user movement classification[C].Evolutionary Computation.IEEE,2015:730-737.
[6] CATENI S,COLLA V,VANNUCCI M.A method for resampling imbalanced datasets in binary classification tasks for real-world problems[J].Neurocomputing,2014,135(8):32-41.
[7] KRAWCZYK B,WOZNIAK M,SCHAEFER G.Cost-sensitive decision tree ensembles for effective imbalanced classification[J].Applied Soft Computing,2013,14(1):554-562.
[8] SAHIN Y,BULKAN S,DUMAN E.A cost-sensitive decision tree approach for fraud detection[J].Expert Systems with Applications,2013,40(15):5916-5923.
[9] LOMAX S,VADERA S.A survey of cost-sensitive decision tree induction algorithms[J].Acm Computing Surveys,2013,45(2):227-268.
[10] 尹华,胡玉平,Yin Hua,等.一种代价敏感随机森林算法[J].武汉大学学报工学版,2014,47(5):707-711.
[11] SAHIN Y,BULKAN S,DUMAN E.A cost-sensitive decision tree approach for fraud detection[J].Expert Systems with Applications,2013,40(15):5916-5923.
作者信息:
张翕茜1,李凤莲1,张雪英1,田玉楚1,2
(1.太原理工大学 信息工程学院,山西 晋中030600;
2.昆士兰科技大学 电机工程及计算机科学学院,澳大利亚 布里斯班4001)

