0 引言

    随着航空技术的发展，无人机在军用与民用领域的应用不断扩大，如：敌情侦察、地形勘探、地理测绘、目标轰炸、高压巡线等^[1-2]。无人机执行的任务复杂多样，为了提高其生存能力，必须实现自主飞行。航迹规划作为无人机自主飞行的关键技术之一，一直是国内外学者们研究的热点。

    航迹规划可以被看作是优化一系列未知航点集的多约束组合问题，据现有的报道，很多人工智能算法可有效解决该问题。例如，XU C等^[3]提出采用人工蜂群算法（Artificial bee colony algorithm，简称ABC）去解决无人机航迹规划问题，并在侦察蜂搜索阶段加入混沌算子，取得了不错的效果；SZCZERBA R J等^[4]在A*算法中添加自适应搜索策略，有效去除了规划空间中的无用航点，提高了算法的搜索时间。然而，上述方法只停留在二维航迹规划层面上，并未考虑规划空间中的地形信息和无人机的拐弯角、俯冲角/爬升角以及最短航迹段长度等约束。而三维航迹规划更符合实际需求，需对其开展研究。近年来，张仁鹏等^[5]在建立地形数字模型的基础上，采用改进粒子群算法来模拟无人机三维航迹规划，获得了安全可飞的航迹；ROBERGE V等^[6]结合遗传算法(Genetic Algorithm，GA)与粒子群算法两者的优势，采用混合算法解决了无人机三维航迹规划问题。然而，上述算法随着搜索空间维数的增加，稳定性和收敛性会随之下降，也会陷入局部最优值。另外，这些研究也未涉及无人机如何应对突发威胁带来的影响。

    本文采用ABC算法来解决无人机的三维航迹规划和针对突发威胁时的航迹重规划问题。同时，为了提供传统ABC算法的收敛性、鲁棒性与稳定性，在雇佣蜂搜索时引入自适应搜索算子、在跟随蜂搜索时引入新型概率选择方式及在侦察蜂搜索时引入混沌算子，从而得到了一种改进的ABC算法(Probability self-Adaptive Chaotic Artificial Bee Colony algorithm，PAC-ABC)。然后，对无人机的规划空间、地形信息和航迹代价模型进行了建模，给出了相应的数学描述。最后，通过三维航迹规划与突发威胁航迹规划模拟，验证了本文所提算法的有效性。

1 航迹规划建模

1.1 规划空间与地形模型

    在三维空间内，无人机航迹规划问题就是利用规划算法找出一系列适合飞行且能满足约束条件的飞行航点集^[7]。在无人机实际应用汇总，规划空间中隐藏着各种威胁信息，如地形、雷达、高炮等，有时这些威胁还具有不确定性，因此想预先获取飞行空间中的威胁信息具有很大的难度。另外，无人机的续航时间很依赖油耗大小。为了简化航迹规划过程，本文提出了以下几个假设条件：(1)所有规划空间内的威胁物与地形信息均一致；(2)无人机的油耗与航程成线性关系；(3)无人机的飞行速度保持恒值不变；(4)忽略阵风干扰、机械动力学及机械振动等因素。

    用点(x_α，y_α，z_α)来表征规划空间的某个航点，其中x_α为经度值，y_α为纬度值，z_α为海拔高度，故航迹规划的规划空间可描述为^[8]：

其中，(x，y)表示山体坐标，(a_k，b_k)为山体中心对称轴坐标，hk为山体的最高点。

1.2 航迹代价模型

    航迹代价模型由威胁代价模型和油耗代价模型组成。其中，威胁代价主要考虑高炮威胁和雷达威胁^[9]。

    (1)雷达威胁。通常雷达的探测范围为圆形，故设雷达对无人机的威胁概率为：

其中，d为雷达中心到无人机的距离，d_max为雷达探测区域的最大半径。

    (2)高炮威胁。和雷达威胁类似，高炮威胁的范围也为圆形，故设高炮对无人机的威胁概率为：

    (3)油耗代价。油耗与航程有关，故认为油耗代价就是总航程。

    另外，还应该考虑无人机航迹规划过程中的其他约束条件：

    (1)极限拐弯角。无人机通过控制其偏航角来控制航向的改变。因为存在惯性，飞行过程中要改变航向需要拐弯时间与拐外半径。记航迹段li在水平面投影为m_i=(x_i-x_i-1，y_i-y_i-1)，设无人机允许的极限拐弯角为θ_t，则该约束可被描述成：

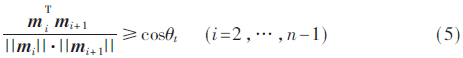
    (2)极限俯冲角/爬升角。无人机在高度方向(z方向)上俯冲与爬升的角度限制于其机动性。因此，可设定极限大俯冲角/爬升角为θ_p的约束方程为：

    (3)最小航迹段长度。在飞行过程中，当前飞行姿态的改变需要无人机持续飞行一段距离，若无人机偏航角改变频繁或者大幅度迂回飞行，则会扩大导航误差，故应尽可能减小航迹长度。设定无人机的最小飞行航迹段长度为l_min，则该约束的数学描述为：

    综上所述，航迹代价模型主要由上述因素构成，故无人机三维航迹代价模型可表示为：

式中，J₁～J₅分别表征飞行过程中的威胁指标、油耗指标、极限拐弯指标、极限俯冲角/爬升角指标与最小航迹长度指标，w_k为相应的权重系数。

2 改进的人工蜂群算法

    ABC算法是由土耳其KARABOGA D教授提出的一种模拟蜂群协作觅食行为的新兴元启发式优化算法^[10]。在算法中，蜜蜂的种类可分为雇佣蜂、跟随蜂和侦察蜂3种。设蜂群种群总数为N，雇佣蜂和跟随蜂的数量各占种群总数的一半；每个蜜源均为一个D维向量，其中D表示需要被优化的解个数。在无人机航迹规划问题，种群中的每只蜜蜂对应一组可行解，ABC算法通过3种蜂种的搜索方式寻找搜索空间的最优解。同时，在算法中添加自适应搜索策略、新型概率选择策略与Logistic混沌搜索算子。具体的步骤如下所示：

    (1)种群初始化。随机派出N只蜜蜂寻找到x_ij(i=1，2，…，N；j=1，2，…，D)蜜源，即可行解。蜜源由式(9)产生：

    (2)蜜源收益度计算。根据式(10)来计算每只蜜蜂初始时搜索到蜜源的收益度值，并根据蜜源大小排序，取前N/2组解。

其中，S_i是ABC算法中的目标函数值。

    (3)雇佣蜂搜索阶段。在此搜索阶段，蜜源信息会因为雇佣蜂的过度挖掘而致使算法迭代速率降低^[11]，故本文采用一个自适应搜索策略来改进原搜索方式，即：

    (4)跟随蜂搜索阶段。随着算法迭代次数的增加，种群个体虽会朝着一个方向进化，但同时也会遗漏其他有用信息，从而导致种群多样性的降低。ABC算法性能的提高在某种程度上依赖于种群多样性。研究发现，被摒弃的解也含有有用信息^[12]。所以，为了使含有较差信息的蜜源同样能被充分挖掘，本文采用一个新颖的概率选择方式，来保证种群的多样性：

    (6)记录当前最优解。当算法遇到终止条件时，输出迭代过程中的最优解。

3 仿真实验

    在本节中，通过一个三维航迹规划仿真算例对本文所提PAC-ABC算法的有效性进行验证。另外，也引入传统ABC算法与GA算法与之进行比较分析。规划空间采用100 km×100 km×100 km的三维空间。空间中共有5座山峰，叠加的地形信息参数为：

    另外，威胁物中的雷达和高炮的分布信息如表1所示。

    无人机飞行的起始点为(0，0，0)，目标点为(90，80，0)，规划的维数D=10。采用PAC-ABC算法、ABC算法和GA算法同时去搜索最优航迹。前两种算法的初始条件设置为：N=20，limit=15。而设置GA算法的条件为：抗体种群数M=20，交叉因子与变异因子分别为0.8与0.2。3种算法各运行10次，每次迭代500次，然后记录下其中的最优解。航迹规划的结果如图1所示。从图中可以看出，3种算法均能生成可飞航迹，但是ABC算法与GA算法获得航迹均要翻越山脊，这会导致无人机被发现的概率增加；而PAC-ABC算法获得航迹则沿着山谷飞行，并较其他两种算法缩短了航程，利于规避威胁，实现低空突防。

    图2给出了3种算法的迭代曲线，从图中可以看出本文所提算法的收敛速度最快，在100代左右就能收敛到极值，且航迹代价为51.231 2，而ABC算法和GA算法的航迹代价分别为54.998 0和60.621 4。在改进策略的作用下，PAC-ABC算法能够较好地避免局部最优值，迅速地寻找到最优解。

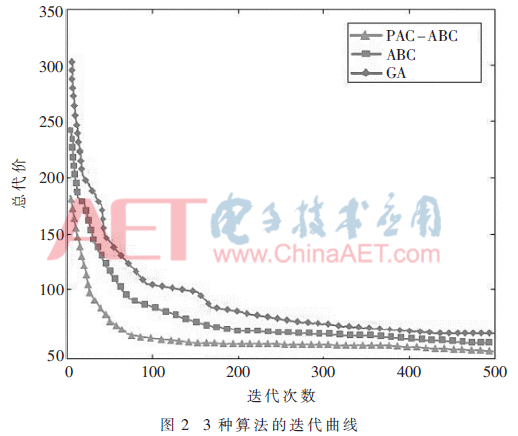
    为了进一步验证PAC-ABC算法的鲁棒性，分别取D为20和30时，评价此算法求解无人机航迹规划问题的效果，仿真结果如图3所示。从图中可以看出，随着维数的增加，PAC-ABC算法依旧能够寻找到较好的航迹。这说明本文所提算法具有较好的鲁棒性。

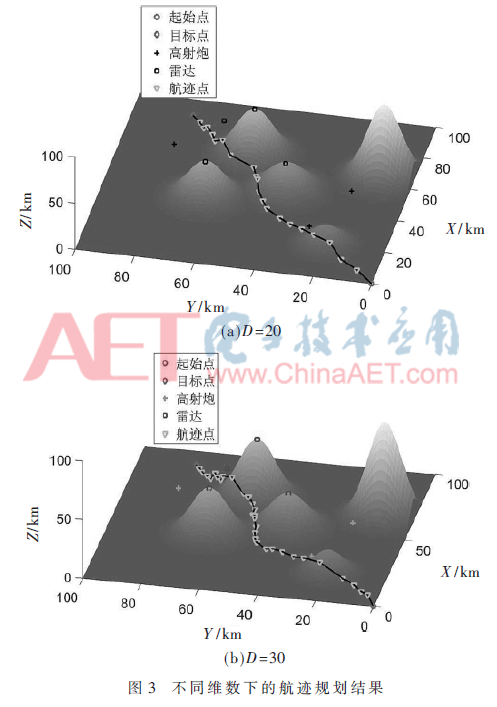
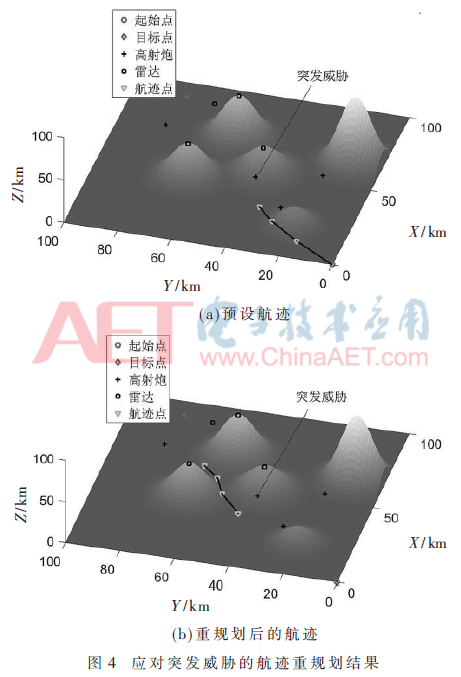
    有时，在规划空间中隐藏着未被发现的突发威胁。当无人机遇到这些突发威胁时，需要算法具有重规划能力，来规避这些威胁。设无人机从起始点(0，0，0)到目标点(90，80，0)中，在(40，40，13)点处突然侦察到高炮，如图4(a)所示。若不改变航迹继续飞行，无人机则有几率被击落，故需要对其航迹重新规划。如图4(b)所示，通过PAC-ABC算法对航迹再次规划，可以有效避免突发威胁，规划时间仅为1.24 s。这说明本文所提航迹规划算法迭代速率高，具有一定的实时性。

4 结论

    在处理无人机三维航迹规划问题时，本文提出了一种改进人工蜂群算法。在算法中，通过自适应搜索策略、新颖的概率选择方式以及混沌搜索算子，提高了算法的稳定性、搜索快速性与鲁棒性。三维航迹规划实验表明：(1)与ABC算法与GA算法相比，PAC-ABC算法能够更快地获得最优航迹，且航迹代价分别比前两者少7.35%和18.33%；(2)随着解维数的增加，PAC-ABC算法依旧能够获得较好的解，具有很强的鲁棒性；(3)在处理突发威胁时，PAC-ABC算法能够在较短的时间内实现局部航迹在规划，保证了无人机的安全飞行。综上所述，本文所提算法能够为无人机规划出一条可飞且较优的飞行路径。

参考文献

[1] CHEN Y，LUO G，MEI Y，et al.UAV path planning using artificial potential field method updated by optimal control theory[J].International Journal of Systems Science，2016，47(6)：1407-1420.

[2] GEVAERT C M，PERSELLO C，SLIUZAS R，et al.Informal settlement classification using point-cloud and image-based features from UAV data[J].ISPRS Journal of Photogrammetry and Remote Sensing，2017，125(3)：225-236.

[3] XU C，DUAN H，LIU F.Chaotic artificial bee colony approach to uninhabited combat air vehicle(UCAV) path planning[J].Aerospace Science and Technology，2010，14(8)：535-541.

[4] SZCZERBA R J，GALKOWSKI P，GLICKTEIN I S，et al.Robust algorithm for real-time route planning[J].Aerospace and Electronic Systems，IEEE Transactions on，2000，36(3)：869-878.

[5] 张仁鹏，杨金孝，潘佳华，等.基于改进粒子群算法的无人机三维航迹规划[J].计算机仿真，2014，31(3)：66-69.

[6] ROBERGE V，TARBOUCHI M，LABONTE G.Comparison of parallel genetic algorithm and particle swarm optimization for real-time UAV path planning[J].IEEE Transactions on Industrial Informatics，2013，9(1)：132-141.

[7] BESADA-PORTAS E，DE LA TORRE L，MORENO A，et al.On the performance comparison of multi-objective evolutionary UAV path planners[J].Information Sciences，2013，238(7)：111-125.

[8] 胡中华.基于智能优化算法的无人机航迹规划若干关键技术研究[D].南京：南京航空航天大学，2011.

[9] DUAN H，ZHANG X，WU J，et al.Max-min adaptive ant colony optimization approach to multi-UAVs coordinated trajectory replanning in dynamic and uncertain environments[J].Journal of Bionic Engineering，2009，6(2)：161-173.

[10] KARABOGA D，BASTURK B.On the performance of artificial bee colony(ABC) algorithm[J].Applied Soft Computing，2008，8(1)：687-697.

[11] FOO J L，KNUTZON J，KALIVARAPU V，et al.Path planning of unmanned aerial vehicles using B-splines and particle swarm optimization[J].Journal of aerospace computing，Information，and Communication，2009，6(4)：271-290.

[12] 林小军，叶东毅.云变异人工蜂群算法[J].计算机应用，2012，32(9)：2538-2541.

[13] CHEN G，WU X，ZHU X，et al.Efficient string matching with wildcards and length constraints[J].Knowledge and Information Systems，2006，10(4)：399-419.

作者信息:

叶  春1，张曦煌2

（1.江苏信息职业技术学院 物联网工程学院，江苏 无锡214001；2.江南大学 物联网工程学院，江苏 无锡214001）