文献标识码: A
DOI:10.16157/j.issn.0258-7998.174068
中文引用格式: 苏智超,黄新敬,薛亚萌,等. 基于球形内检测器的管道倾角测量新方法[J].电子技术应用,2018,44(5):93-97,102.
英文引用格式: Su Zhichao,Huang Xinjing,Xue Yameng,et al. A new pipeline inclination measurement method using spherical inner detector[J]. Application of Electronic Technique,2018,44(5):93-97,102.
0 引言
管道是输送石油、天然气和水等资源的主要方式。经过多年发展,我国的油气管网规模已经非常庞大,目前有66%的管道已服役超过了25年[1]。但管道受输送介质、输送工况、地理气候变化、人为破坏和施工的影响,随着使用年限的增加,会逐渐出现焊缝开裂、腐蚀穿孔和形变等现象[2]。定期检测是确保管道长期安全运行的有效措施,而管道故障检测只有在已知管道地理坐标的前提下才有意义。受敷设装备和工艺等因素制约,部分管道在敷设时偏离设计路由。尤其对于海底管道,在海流和海床运动的影响下[3],极易发生位移和形变,这都导致了原有地理坐标信息的丢失。因此对管道进行精确定位有着重要的现实意义[4]。
2004年,李孟杰等[5]研究设计了GPS、SINS与极低频电磁示踪相结合的海底管道轨迹在线测量系统:内检测器PIG携带电磁发射机和惯性测量单元(Inertial Measurement Unit,IMU)在海底管道内间歇行进;跟踪船携带电磁接收机和GPS接收机跟踪和定位PIG。该方法理论上能够连续测量整条管线坐标,但精度不详,运行过程中需要跟踪船配合作业,效率很低。2011年,Jin Shiyong等[6]研究了基于SINS的海底管道轨迹描述技术,通过实验校准,测得的管道轨迹偏差基本满足误差要求,但具体校准方法和定位精度不详。2012年沈阳工业大学的杨理践教授等[7-9]针对PIG的运行规律、离线数据处理以及无法利用GPS和地磁导航等特点,全面系统地研究了基于IMU/里程仪组合导航的管道三维地理坐标测量技术,目前精度为管长400 m时误差为0.16%,仍然满足不了长输管道的检测需求。
2014年陈世利等[10]提出了一种球形内检测器用于检测和定位管道微小泄漏,具有不易卡堵、信噪比高的优点。随后黄新敬等[11-13]提出了一种通过管道内磁场反演计算管道三维走向及地理坐标测量的方法,30 km管道轨迹重构误差为1.2 km,但在倾角测量方面表现不够理想,测量精度欠佳。管道定向及定位主要利用管道的倾角、偏角和内检测器的里程数据计算,由于很难在现场对管道地磁屏蔽模型进行标定,所使用的理想屏蔽系数与实际值存在一定偏差,因此在管道倾角测量上存在较大误差,从而导致管道地理坐标测量误差较大[14]。
本文针对上述方法存在的不足,利用球形内检测器在管道中的运动特点、磁化后管道内的磁场特征和坐标变换,提出了一种不使用管道磁屏蔽模型的管道倾角测量新方法。
1 测量原理
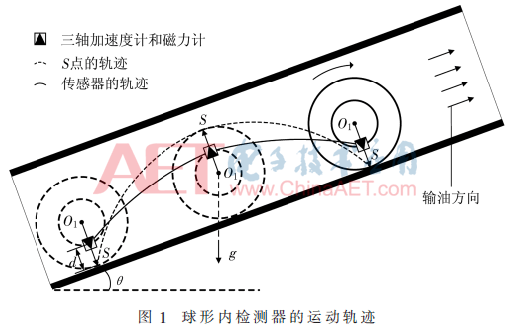
现场实验证实球形内检测器在滚动过程中短时间内绕某一固定轴旋转,可用于球体姿态反演;球形内检测器中的传感器所在位置不在球体中心,测点轨迹是一条摆线,如图1所示;当管道具有原始磁化或经历过特殊磁化,管道内径向磁场将存在梯度,磁传感器测量值的大小与距离管壁的远近有关。因此,可充分利用重力场和磁场梯度来解算球体姿态和管道倾角。
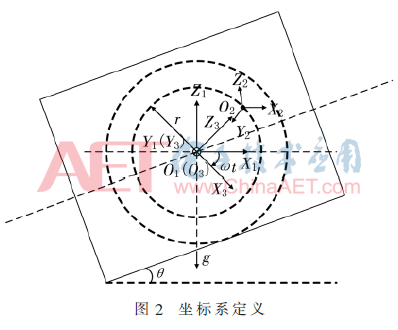
基于以上条件,建立求解管道倾角的数学模型。坐标系定义如图2所示。定义管道坐标系O1-X1Y1Z1,其中X1平行于水平面,Y1垂直于管道轴向向里,Z1竖直向上与重力加速度反向。内检测器搭载一个九轴加速度计-陀螺仪-磁力计JY901,传感器在管道内绕定轴旋转运动,旋转半径为r,定义传感器的加速度测量轴为坐标系O2-X2Y2Z2,该坐标系的方向与传感器在内检测器内的装配角度有关。传感器可测得在坐标系O2-X2Y2Z2下以角速度ω旋转的磁场B2和加速度a2,磁力计与加速度计的测量轴完全一致。定义内检测器体坐标系O3-X3Y3Z3,其中Z3指向坐标系O2-X2Y2Z2的原点O2,Y3与Y1重合,二者所在的轴线即传感器旋转所围绕的固定轴线。
在O1-X1Y1Z1坐标系下对O3-X3Y3Z3坐标系的三轴定义为:
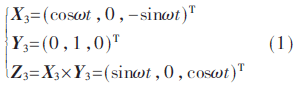
从O3-X3Y3Z3坐标系变换到O1-X1Y1Z1坐标系的旋转矩阵为:



加速度的输出为:

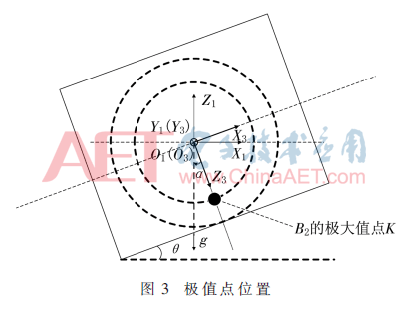
其中Z3轴与重力加速度之间的夹角为α,根据图3中的几何关系,α与θ相等。
2 仿真模型
针对管道单侧磁化后管道径向磁场不均匀的特点,对管道内磁场及传感器数据进行了仿真分析。管道及坐标系定义如图4所示。
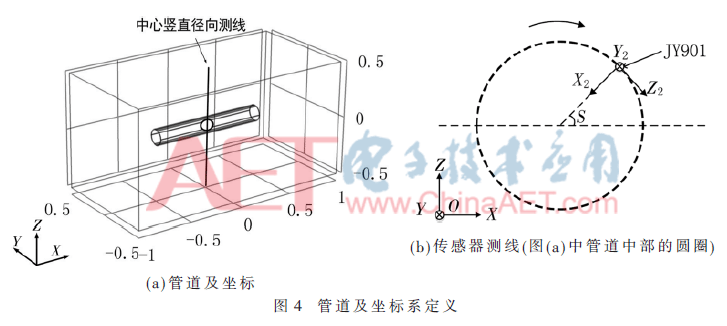
2.1 管道内磁场仿真
仿真管道模型:管道长度为1 m,外径为140 mm,壁厚5 mm,相对磁导率为200。
管道底部单侧磁化仿真:在无地磁场的情况下,首先在管道底部施加沿-X方向的磁化,磁化强度为300 000 A/m;然后把该区域沿Y=0截面分成两部分,Y>0的部分施加Y方向磁化,Y<0的部分施加-Y方向磁化,磁化强度均为600 A/m。此时,管道内磁场值接近于实际值。
仿真结果:
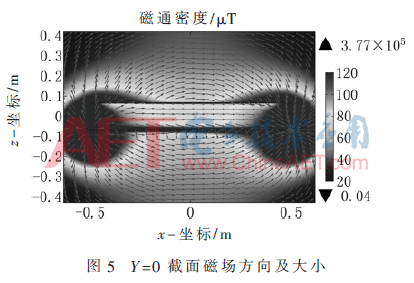
(1)Y=0截面磁场分布如图5所示,说明除去管道两端,管道中磁场大部分在轴向上是均匀的。
(2)图4(a)中心竖直径向测线的磁场大小如图6所示,说明离被磁化的管道底部越近,磁场越强。

在实验室条件下,无法实现让球形内检测器在管道内匀速滚动。基于仿真结果,可利用传感器在管道中部原位置的旋转代替内检测器滚动前行。
2.2 传感器数据仿真
根据2.1节管内磁场仿真结果,可利用传感器在管道中部原位置的旋转代替内检测器滚动前行。旋转半径为4 cm,根据式(8)可以仿真出传感器在旋转时的磁场测量值和加速度测量值。

仿真结果如下:
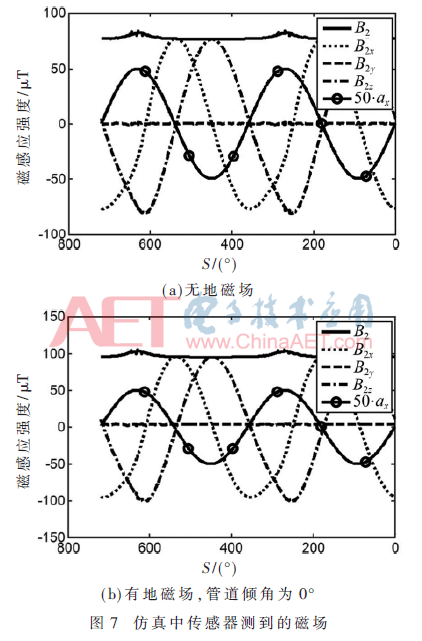
(1)传感器在两个周期(S=720°→0°)内测得的磁场和传感器X轴测得的加速度值ax如图7(a)所示,加入地磁场后如图7(b)所示,各轴幅值均增加,由于管道的磁屏蔽作用,B2y增加很小。图7表明:在传感器接近被磁化一侧的管壁时,波形发生畸变。因为传感器旋转平面的磁场可以分解成-Z方向和X方向,在旋转过程中,X方向的磁场大小不变,而-Z方向磁场分量随着Z坐标的减小而增大,所以B2z和B2x的波形发生了畸变。同时,B2的极大值点对应离被磁化管壁最近点(S=630°,270°)。
(2)图8表明:B2的极大值点不会随倾角变化发生偏移,因此该点与管道的相对位置保持不变,始终对应被磁化管壁最近点。
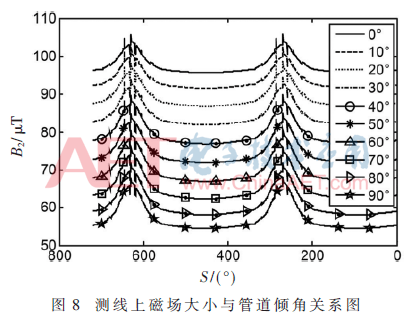
根据结果和式(7)可知,当管道倾角不同时,B2的极大值点在管内的位置不会发生变化,但是该点对应的Z3会随管道倾角变化,且与管道倾角一一对应,从而验证了该方法的可行性。
3 管道倾角测量实验
3.1 实验过程
退磁处理,使用退磁器将管道(45#钢无缝钢管,长度为1 m,外径为140 mm,壁厚5 mm,管道中部钻8 mm的通孔)进行全面退磁;进行磁化,磁化方式为使用一块长50 mm、宽20 mm、厚10 mm的钕铁硼强磁铁(表面高斯3 291 Gauss,最大磁能积35 MGOe)N极吸附在底部一端,然后沿直线匀速滑行至另一端(从南到北),完成磁化,磁化方向与仿真一致。
采用直径为6 mm的铝棒连接传感器和步进电机;步进电机端采用梅花型联轴器连接铝棒;步进电机驱动传感器转动。传感器通过蓝牙向上位机传输数据。
设置旋转角速度为720 °/s(接近于现场实验中的球型内检测器的转速)。实验测量0°~90°共10组不同倾角,每组倾角测量取20个测量周期的平均值。
传感器实测波形如图9所示。结果表明,对比图9(a)与图7,仿真结果与实验结果中各轴的波形吻合度较高。

3.2 实验结果
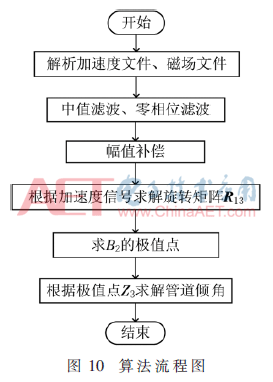
对传感器数据进行处理,算法流程如图10所示。其中,中值滤波用于平滑加速度信号;零相位滤波用于消除随机白噪声,因为加速度和磁场信号各分量之间有严格的相位差,这是寻找极值点的依据,所以使用零相位滤波器保证滤波后各分量之间的相位差不会发生变化。在进行滤波的过程中,通常会使信号的幅值发生改变,而加速度信号各个分量的幅值对于本方法是不允许发生畸变的,因此要对信号的幅值进行补偿。同时,要对滤波后的磁场信号进行系数校正[15],因为在相位差不变的情况下,磁场各轴分量的幅值对磁场总量的波形会有较大影响。
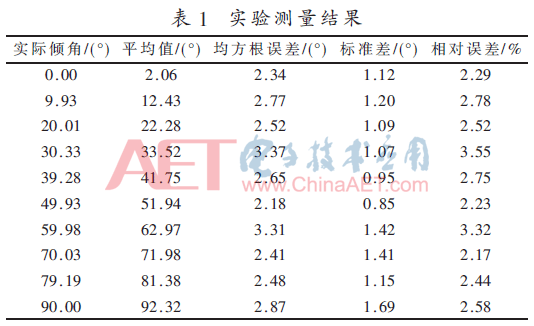
倾角实验测量结果如表1所示。结果表明,倾角实验测量结果中最小标准差为0.85°,最大标准差为1.69°,说明该方法的测量精密度较高;最小均方根误差为2.18°,最大均方根误差为3.37°,说明该方法准确度较高。
4 结论
本文提出了一种在单侧磁化管道的基础上利用球形内检测器测量管道倾角的新方法,并建立了相关数学模型。通过仿真和实验验证了该方法的正确性和可行性。实验结果表明:该方法测量精度较高,倾角测量的最小相对误差为2.17%,最大相对误差为3.55%,可有效提高球形内检测器在测量管道倾角时的精度,有助于管道地理坐标的精确测量,从而准确定位管道故障坐标,保障管道安全运行。
参考文献
[1] 陈世利,谭皓予,李健,等.一种基于ARM-Linux的分布式管道泄漏监测系统[J].电子技术应用,2011,37(10):73-76.
[2] 余永辉,涂巧玲,彭宇兴.输油管道泄漏检测与定位系统中的相关分析法研究[J].电子技术应用,2009,35(2):128-130.
[3] 欧阳侃夫,杨建钦.GIS在海管完整性管理中的应用[J].微型机与应用,2013,32(23):1-2,6.
[4] 刘渊.管道内球形检测器数据采集平台的研究[D].天津:天津大学,2012.
[5] 李孟杰.海底管道轨迹在线精确测量技术研究[J].中国海洋平台,2004,19(6):46-49.
[6] Jin Shiyong,Ping Yang.Research on the describing of trajectory for subsea pipeline based on inertial navigation system[C].Power Engineering and Automation Conference.IEEE,2012:463-468.
[7] Li Hui,Jin Peng.Initial alignment of SINS in the measurement system of pipeline position based on SUKF[J].Applied Mechanics & Materials,2014,568-570(14):464-467.
[8] 杨理践,李晖,靳鹏,等.管道地理坐标测量系统SINS安装误差标定[J].仪器仪表学报,2015,36(1):40-48.
[9] 杨理践,沈博,高松巍.基于组合导航技术的管道地理坐标定位算法[J].沈阳工业大学学报,2014,36(1):66-71.
[10] 陈世利,黄新敬,郭世旭,等.海底管道微泄漏球形内检测器可行性研究[J].石油工程建设,2014,40(2):19-26.
[11] 陈冠任,李健,黄新敬,等.基于球形内检测器的管道内磁场测量简[J].传感技术学报,2016,29(10):1486-1492.
[12] 赵伟,曾周末,陈世利,等.管道内地磁场特性分析及实验研究[J].仪器仪表学报,2012,33(7):1556-1560.
[13] Huang Xinjing,Chen Shili,Guo Shixu,et al.A 3D localization approach for subsea pipelines using a spherical detector[J].IEEE Sensors Journal,2017,17(6):1828-1836.
[14] Huang Xinjing,Chen Guanren,Zhang Yu,et al.Inversion of magnetic fields inside pipelines:modeling,validations,and applications[J].Structural Health Monitoring,2017,17(1):80-90.
[15] 黄新敬.海底管道地理坐标测量技术研究[D].天津:天津大学,2015.
作者信息:
苏智超,黄新敬,薛亚萌,陈冠任,陈世利,曾周末
(天津大学 精密仪器测试技术及仪器国家重点实验室,天津300072)

