0 引言

    人工势场法是一种结构简单的运动规划算法，具有鲁棒性强、路径平滑、执行效率高的优点^[1]，但在实际应用中常在障碍物周围产生局部振荡。目前，国内外许多学者对此进行了探索研究，常见的改进思路有增加虚拟障碍物、建立虚拟目标点、改变势函数等^[2-3]，其适用面窄、通用性差，很难实现振荡区域边界点的精确定位。RRT算法在运动规划中具有良好的扩展性和搜索速度，与人工势场的结合可使路径快速跳出局值吸引区，但逃离点落在狭缝之中或其附近时RRT算法易陷入局部死循环^[4-6]。针对这些不足之处，本文提出一种基于旋转速度矢量角的人工势场和TAS-RRT融合优化算法，当陷入局部振荡时，以旋转速度矢量角分析运动趋势、精确定位逃离点，并使用速度矢量角度差引导RRT采样的分布、调节局部规划器的连接方式，使其采样的方向快速逼近逃离点，当采样点满足条件时，切换回人工势场算法进行运动规划。程序运行结果表明，该算法搜索效率高，复杂环境下依然有效。

1 改进人工势场

1.1 人工势场

    传统人工势场是一种虚拟势场^[7]，包括吸引势场f_a(x)和抵制势场f_t(x)： 

1.2 旋转速度矢量角

    针对人工势场易陷入局部振荡的问题，本文提出一种旋转速度矢量角方法，将其作为跳出极小值吸引区域的判断条件，如图1所示，其中点Root代表局部极小值点；current为当前访问节点，V₁为位于点current位置时对应的速度矢量；Next1为下一个访问节点，V₂为对应的速度矢量；Next2为机器人位于点Next1位置时下一个访问节点，V₃为对应的速度矢量。

说明节点运动趋势为远离极值点，且其趋势不断增强，则当前节点current为局部极小值吸引区的跳出点，切换回人工势场算法进行运动规划。

2 基于速度矢量角度差引导的快速随机扩展树改进算法

2.1 RRT算法

    RRT算法以构型空间中的初始状态xs为起始点构建随机扩展树，初始化后通过迭代的方式向外扩展，在环境范围内随机采样自由节点q_rand，遍历树T的所有节点，选择其中离q_rand最近的节点q_near，其后通过Extend(q_rand，q_near)函数检验两节点的距离是否满足要求，若满足q_rand即为q_new，否则沿着q_near至q_rand取距离为δ的状态节点作为q_new，利用局部规划器对q_new和q_near之间的路径进行检测，若无障碍碰撞，将其作为新的节点添加到扩展树上，并更新父节点和新树枝长度。

    重复上述过程，直到满足stopcondition：新状态节点与x_g构建路径成功或者超过最大迭代次数，结束扩展。图形建立完毕后，利用搜索算法即可得到x_s和x_g间最短规划路径。具体搜索过程如图2所示。

2.2 TAS-RRT算法

    RRT算法规划的路径质量不高且狭缝通道难以穿越，针对以上缺点，本文提出一种基于速度矢量角度差引导的快速随机扩展树算法，在采样的过程中引入速度矢量角度差，将其作为判断采样点有效性的条件，并根据潜在节点的状态调节树的规划器以改变扩张速度。

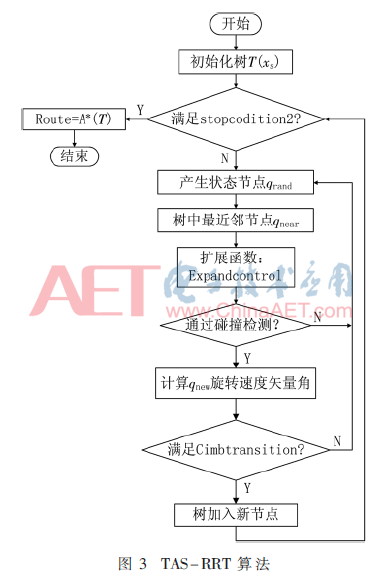
    具体搜索过程如图3所示。将局部极小值点作为构建扩展树的起点，初始化后以迭代的方式向外扩展，在环境内随机采样自由点q_rand后选择树中最近节点q_near，其后Expandcontrol(q_rand，q_near，T)函数驱使规划器自适应地选择探索速度，选择依据为树的爬坡状态。若是细化节点爬坡失败，即潜在采样节点参数θ₁减小，则转换为扩张状态，否则全部继续细化树枝。其中q_near和q_rand的距离函数可以预估下一步是细化还是扩张，若距离比扩张步delta高，那么参与树的扩张，相反，距离小于delta，认为节点参与树的细化。沿q_near至q_rand取点q_new使其满足距离条件，若q_new和q_near之间的路径无障碍碰撞，计算节点q_new的速度矢量角度差θ₁，并通过函数Climbtransition(θ₁，T)过滤节点，使其按照速度矢量角度差增长方向爬坡，以此引导节点采样，直到满足stopcondition2：到达目标状态节点附近或者满足转换条件，即式(8)。

3 贪心细分后处理算法

    采用TAS-RRT算法跳出局部极小值陷阱，可能导致路径绕行，且随机树的采样特性容易产生冗余采样，因此本文引入细分贪心方法对节点进行后处理，如图4所示，其中Root为局部极小值节点，Jump为采用旋转速度矢量分析定位的吸引区跳跃点，实线为初始规划路径，由于节点的冗余主要来自于跳出极值吸引区的过程，所以对Jump节点进行两次细分贪心后处理。

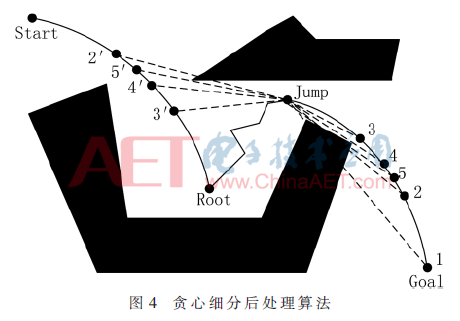
    首先，对节点Jump和Goal之间的路径进行分段处理，初始化节点behind，即为节点Jump，节点current从Goal开始取点，循环过程为连接Jump和current，并判断是否与障碍物碰撞，若是front=current，继续循环直到判断结果为否，则behind=current，循环结束。其后取behind和front中间节点为current，连接节点Jump和current，判断节点Jump和current连线是否与障碍物碰撞，若是更新front=current，若否则更新behind=current。其后继续循环取中间节点直到满足stopcoditon3，最终取邻节点next1=behind，文中stopcoditon3为循环次数；图中从目标点Goal开始取值并与节点Jump连接，最终Jump的邻节点next1为behind=4。

    其后，对Jump和Start之间的路径进行第二次细分贪心处理，取behind=Jump，current从Start取点，与第一次细分贪心处理不同之处在于，满足循环次数后，继续执行判断3：邻节点next2是否为TAS-RRT算法产生的采样节点，若是，继续对next2进行细分贪心后处理即初始化behind=next2，从Start取点current并判断next2与current是否碰撞，不断循环直到判断3结果为否，更新相应的邻节点。图4中Jump经过第二次细分贪心处理后next2为节点5′，由于5′不是扩展树采样节点因此循环结束，图中后处理路径采用粗虚线连接。

4 仿真实验

4.1 旋转速度矢量角法的适用性和有效性

    结合目标位置和环境障碍信息，通过势场方程计算各个节点的势场强度，并根据计算的结果调节仿真图以验证融合算法的可行性，选择稀疏Djkstra算法、基于速度矢量角度差引导的稀疏A*算法、RRT算法与改进式人工势场进行混合，并选取具有有代表性的障碍环境以验证算法的性能。

    首先，通过MATLAB建立具有开口凹槽障碍物的地图环境，如图5(a)，并人为设定初始坐标[175，410]和目标点坐标[450，130]，其后分别运用3种混合算法进行路径规划。

其中算法1、算法2和算法3分别表示稀疏Djkstra、稀疏AS-A*、RRT算法与改进人工势场混合优化算法。稀疏Djkstra算法和稀疏AS-A*算法相邻节点间隔均取4，由于RRT算法采样的随机性，算法3进行50次路径规划实验。3种算法失败率为0，结果证明了旋转速度矢量角法的有效性。

    其次，变换地图为更加复杂的多正方形障碍环境，如图5(b)所示，由于障碍物形状和排布特点，始末节点间存在多个局部极小值吸引区域，通过多次实验得到的结果如图5(c)、图5(d)、图5(e)，图中规划路径位于人工势场线中，障碍物附近斥力强、场力线密集。从图5可看出，虽然障碍物数量增加，工作环境更为复杂，但采用多种算法与改进人工势场进行混合优化，依然能够顺利完成避障，而且轨迹较为平滑。

    两种地图环境下对混合算法进行对比，结果如表1所示，其中：算法3的参数取20次实验的平均值；n_to表示生成路径包含的节点总数；t表示算法运行所需总时长；t_es表示跳出局部极小值吸引区域耗费的时间；n_es1表示算法跳出一局部极小值吸引区时采样的节点总数，图5(a)取局部极小值[272，233]，图5(b)取局部极小值[175，325]。

    对比表1中参数可知，运行时间大部分用于跳出局部极小值吸引区域，且无论是简单的地图环境还是复杂的地图环境，改进式人工势场与RRT混合优化算法的参数皆数倍均优于其他算法。再对地图环境、初始坐标和目标点坐标进行多次变换，路径规划依然成功，说明改进人工势场能与多种算法融合并能适应环境的变化。

4.2 快速扩展随机树的优化改进

    将地图环境设置为特殊状态，如图6(a),即起点附近存在局部极小值且始末点间存在长狭缝通道，运用MATLAB对算法3和算法4进行建模仿真，算法3为改进式人工势场与RRT混合优化算法，算法4为改进人工势场与TAS-RRT混合优化算法,两种算法选用参数相同，最大采样次数取300，扩张步长取30，狭缝宽度L取10，结果如图6(b)、图6(c)、图6(d)、图6(e)。从图6(b)、图6(c)可看出改进人工势场与TAS-RRT混合优化算法可快速定位边界点，而改进人工势场与RRT混合优化算法在采样300次后失败。图6(d)为改进人工势场与TAS-RRT混合优化算法的初步路径，图6(e)为其经贪心细分后处理的路径，从两图的对比可以，节点数目明显减少，路径更为平滑。

    进行50次路径规划实验取参数平均值，如表2，表格中算法4取未经贪心细分后处理的数据，在狭缝环境下改进人工势场与RRT混合优化算法成功率为60%，改进人工势场与TAS-RRT混合优化算法成功率为100%。由于算法的差异性主要取决于与人工势场混合的算法的选择，因此表格着重分析跳出极小值吸引区的过程，其中：跳跃过程中改进人工势场与RRT混合优化算法平均采样112个节点，改进人工势场与TAS-RRT混合优化算法平均采样数为14，极大地减少了采样节点数目，且成功跳跃时采样节点平均数目n_route、成功跳跃路径长度L_route、成功跳跃所耗时间t_es的参数性能均优于算法3。

    此时若将狭缝宽度调整为3，其他参数相同，改进人工势场与TAS-RRT混合优化算法结果如图6(f)、图6(g)、图6(h),实验50次算法4成功率为100%，跳出极小值过程中采样节点数目约为14，与狭缝宽度为10时基本相同，但是采样时间增加了约2倍，而改进人工势场与RRT混合优化算法成功率为0。

5 结论

    本文提出一种旋转速度矢量角方法，改进人工势场以解决局部极小值问题，并与多种搜索算法优化融合，通过分析计算以自适应定位逃离点，精确控制复杂环境下的运动规划，仿真结果验证了算法的有效性和通用性；其次针对RRT算法穿越狭缝通道成功几率小、运行效率低等问题，提出TAS-RRT算法跳出极小值吸引区域，以速度矢量角度差引导节点渐近逃离路径，并根据潜在节点的状态调节局部规划器从而改变扩展速度，最后对路径进行细分贪心后处理以过滤冗余节点、平滑路径。利用MATLAB建立特殊障碍环境以验证算法的优越性，实验结果表明，改进人工势场与TAS-RRT混合优化算法不仅成功实现了复杂环境下机器人运动规划的控制，而且与RRT混合优化算法相比，大大提高了收敛速度和运行效率。

参考文献

[1] 刘成菊，韩俊强，安康.基于改进RRT算法的RobotCup机器人动态路径规划[J].机器人，2017，39(1)：8-15.

[2] 汪首坤，朱磊，王军政.基于导航势函数法的六自由度机械臂避障路径规划[J].北京理工大学学报，2015，35(2)：186-191.

[3] 姬伟，程风仪，赵德安，等.基于改进人工势场的苹果采摘机器人机械手避障方法[J].农业机械学报，2013，44(11)：253-259.

[4] QURESHI A H，AYAZ Y.Potential functions based sampling heuristic for optimal path planning[J].Autonomous Robots，2016，40(6)：1079-1093.

[5] WU D，SUN Y J，WANG X，et al.An improved RRT algorithm for crane path planning[J].International Journal of Robotics and Automation，2016，31(2)：84-92.

[6] DU M B，CHEN J J，ZHAO P，et al.An improved RRT-based motion planner for autonomous vehicle in cluttered environments[C].IEEE International Conference on Robotics and Automation. Piscataway，USA：IEEE，2014：4674-4679.

[7] 何兆楚，何元烈，曾碧.RRT与人工势场法结合的机械臂避障规划[J].工业工程，2017，20(2)：56-63.

作者信息:

徐晓慧1，张金龙2

(1.江苏城市职业学院 建筑工程学院，江苏 南京210000；2.南京师范大学 电气与自动化工程学院，江苏 南京210042)