文献标识码: A
DOI:10.16157/j.issn.0258-7998.182027
中文引用格式: 杜勇. 一种新的FIR滤波器系数量化方法[J].电子技术应用,2019,45(4):52-54,59.
英文引用格式: Du Yongn. A new method of filter coefficient quantization[J]. Application of Electronic Technique,2019,45(4):52-54,59.
0 引言
相对于模拟滤波器,数字滤波器具有高精度、高可靠性、可编程改变滤波特性、便于集成等一系列优点,并且理论上可实现近似理想频率特性的滤波性能。经典的数字滤波器主要包括有限脉冲响应(Finite Impulse Response,FIR)滤波器和无限脉冲响应(Infinite Impulse Response,IIR)滤波器。相对于IIR滤波器来说,当FIR滤波器系数保持线性对称结构时,能够在满足幅频响应要求的同时获得严格的线性相位特性。在数据通信、语音信号处理、雷达信号处理等领域通常要求信号在传输过程中不能有明显的相位失真,因此FIR滤波器获得了更广泛的应用[1]。
FPGA因其独特的可编程结构及强大的并行运算能力,很适合于实现FIR滤波器设计。基于FPGA的FIR滤波器设计近年来一直是学者们研究的热点,主要集中在最优滤波器设计方法、提高滤波器运行速度、滤波器系数量化方法等方面[2-7]。常规的系数量化方法仅关注对滤波器本身幅频特性的影响[8],较少考虑在滤波器输出位宽确定的情况下,如何提高输出幅度,进而最大化输出信噪比的问题。在研究分析传统滤波器系数量化方法的基础上,提出了基于滤波器增益的系数量化方法,给出了MATLAB及FPGA实现后的ModelSim仿真测试数据,结果表明这种方法最多可将滤波输出幅度提高近一倍,信噪比提高近6 dB。
1 FIR滤波器原理及结构
FIR滤波器,是指单位脉冲响应长度有限的滤波器。FIR滤波器的突出特点是其单位取样响应h(n)是一个N点长的有限长序列,0≤n≤N-1。滤波器的输出y(n)可表示为输入序列x(n)与单位取样响应h(n)的线性卷积。

从系统函数很容易看出,FIR滤波器只在原点上存在极点,这使得FIR滤波器具有全局稳定性。FIR滤波器是由一个抽头延迟线加法器和乘法器的集合构成的,每一个乘法器的操作系数就是一个FIR系数。因此,FIR的这种结构也被人们称为抽头延迟线结构。图1是FIR滤波器FPGA实现的典型结构图。

2 系数量化对FIR滤波器性能的影响
2.1 FIR滤波器的MATLAB设计方法
在采用FPGA编程实现FIR滤波器之前,通常采用MATLAB软件设计滤波器系数。MATLAB提供了丰富的FIR滤波器函数,分别对应不同的设计方法,如窗函数法、频率取样法、基于“最大误差最小”的最优设计法等。为便于对比,采用最优设计方法设计FIR低通滤波器(MATLAB设计函数为firpm),其参数为:采样频率32 MHz,过渡带0.5 MHz~1.5 MHz。图2为MATLAB设计出的滤波器幅频响应图。

由图2可知,FIR滤波器的长度N越大,滤波器过渡带越接近设计参数,通带及阻带滤波性能越好,当N=41时阻带衰减为26 dB,当N=61时阻带衰减为38.5 dB,当N=81时阻带衰减为48 dB;当系数长度超过一定值后(本实例为61),滤波器过渡带的改善余量已很小,但通带及阻带滤波性能会持续增加。不失一般性,下文以长度为61的低通滤波器为例进行讨论。
2.2 系数的量化方法及其对滤波性能的影响分析
根据MATLAB的FIR滤波器设计原理,无论滤波器长度多长,滤波器通带内增益均为1(0 dB),滤波器系数为带小数的浮点数。由于FPGA只能处理二进制数据,MATLAB设计出的滤波器系数需要转换成二进制数据才能完成FPGA电路实现。
滤波器系数是带符号的数据,FPGA实现时需要用二进制补码格式表示。设滤波器系数的量化位宽为Q,则系数C的表示范围为-2Q-1≤C≤(2Q-1-1),又由于FIR滤波器系数的严格对称特性,实际范围为(1-2Q-1)≤C≤(2Q-1-1)。
传统的滤波器系数量化方法可分解为3个步骤:(1)找出滤波器系数中最大的绝对值数M;(2)以M为基准,对所有滤波系数进行归一化处理,即对所有系数除以M;(3)对所有滤波器系数乘以(2Q-1-1),并对处理后的系数取整形成整数系数;(4)将整数滤波器系数转换成二进制补码数据。图3为不同量化位宽情况下的滤波器幅频响应图。
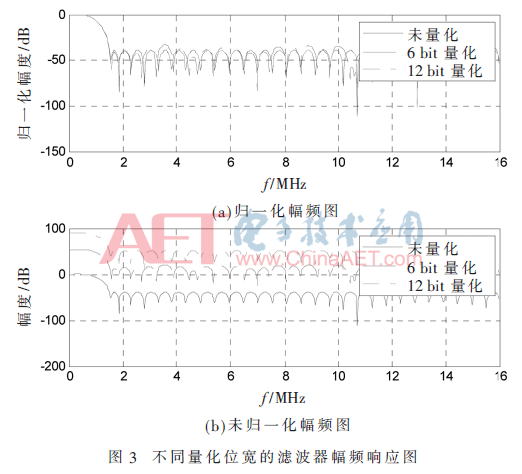
由图3(a)中的归一化幅频图可知,滤波器系数量化位宽越小,量化后的滤波性能越差(当量化位宽为6 bit时,阻带衰减相比量化前减小了约6 dB),反之量化位宽越大,量化前后的滤波性能相差越小。当量化位宽超过一定值(本实例为12 bit)后,滤波性能几乎不再变化。不失一般性,下文以长度为61、量化位宽为12 bit的低通滤波器为例进行讨论。
3 基于增益的FIR滤波器系数量化方法
3.1 一般量化方法对系统性能的影响
根据前面讨论的滤波器量化方法,系数量化过程相当于滤波器增益扩大了(2Q-1-1)/M倍。从图3(b)中的未归一化幅频图可知,量化位宽越大,滤波器通带内的增益越大。当量化位宽为6 bit时,通带增益为54 dB,当量化位宽为12 bit时,增益为90 dB。
FPGA设计FIR滤波器,一般采用定点二进制数据进行运算。前面讨论系数量化对系统性能的影响时,实际有一个前提条件,即滤波运算采用全精度运算,滤波运算的结果保留全部有效数据位。当滤波器系数量化位宽为Q时,由于滤波器增益扩大了(2Q-1-1)/M倍(一般来说,M≤1),为保证全精度运算,保留全部有效滤波输出位宽,相对于滤波器输入信号而言,位宽将增加Qa bit。其中

对于前面讨论的长度N=61,量化位宽Q=12的低通滤波器而言,M=0.062 1,(2Q-1-1)/M=32 963,则滤波输出位宽需增加Qa=16 bit。假设输入数据位宽为10 bit,则滤波器全精度输出位宽为26 bit。

3.2 基于增益的系数量化方法
根据前面的讨论,量化滤波器系数后,输出有效位宽所能表示信号的信噪比下降,是由于滤波输出信号达不到满量程状态。为此,优化滤波器系数量化方法,采用基于滤波器增益的方法对系数进行量化。结合前述的滤波器实例,具体步骤为:(1)对所有滤波器系数乘以 =216=65 536,并对处理后的系数取整形成整数系数;(2)将整数滤波器系数转换成二进制补码数据。
=216=65 536,并对处理后的系数取整形成整数系数;(2)将整数滤波器系数转换成二进制补码数据。
经过改进的量化处理后,相当于对滤波增益直接增加了65 536倍(常规方法仅增加了32 963倍),滤波输出的数据幅值能够达到输出数据有效位宽所能表示的满量程值,实现了输出位宽一定的条件下,输出信号信噪比的最大化。经过这样的量化处理,系数的量化位宽为:

对于上文所讨论的低通滤波器,量化位宽需要13 bit。图4为常规量化方法和改进量化方法的滤波器系数(冲激响应)图,其中Qa=16。

从图4可以看出,在滤波输出位宽相同的条件下,改进的量化方法所产生的滤波器系数(冲激响应)幅值大于常规方法,相当于滤波器增益更大。同时也要注意到,改进的量化方法所需的滤波器系数位宽由12 bit增加到13 bit。也就是说,增加滤波器增益,是以增加系数量化位宽为代价的。
4 FPGA实现后的测试结果分析
接下来采用Xilinx的Spartan6系列FPGA器件XC6SLX25-FT256C为目标平台,调用ISE14.7工具中的FIR滤波器核,实现前文所讨论的低通滤波器(采样频率为32 MHz,过渡带为0.5 MHz~1.5 MHz,滤波器长度N=61)。仿真工具为ModelSim10.1,输入信号为2路单频信号的叠加。两路单频信号频率分别为0.22 MHz和2 MHz,功率比为1:1。输入位宽为10 bit,滤波器输出位宽为26(Qa=16)。图5、图6分别为常规量化方法和改进量化方法的滤波器ModelSim仿真波形图。


从图5、图6中可以看出,两种方法都能够有效滤除带外干扰信号(2 MHz单频信号),改进量化方法的滤波器输出信号幅度值(16,641,407)明显大于常规量化方法的幅度值(7,910,390),相当于增加了滤波增益,增加了滤波输出信号的信噪比。
5 结论
本文详细分析了滤波器系数量化方法对滤波性能的影响。在对常规系数量化方法的步骤、原理进行分析的基础上,针对滤波输出数据幅值达不到有效位宽满量程的现象,提出了基于滤波器增益的系数量化改进方法。MATLAB仿真及FPGA实现后的ModelSim仿真均表明,在滤波输出位宽相同的条件下,改进的量化方法可以有效提高滤波器增益,进而提高滤波输出信号的信噪比。需要注意的是,增加滤波器增益是以增加系数量化位宽、增加FPGA实现后的逻辑资源为代价的。
参考文献
[1] 高耀鸿.基于FPGA的FIR低通滤波器[D].长沙:湖南大学,2012.
[2] 朱效效,蔡俊,陆伟.基于优化DA算法滤波器的设计及其FPGA实现[J].电子技术应用,2015,41(2):59-60,64.
[3] 徐彦凯,双凯.提高定点精度的FPGA信号处理算法[J].计算机工程与科学,2012,34(9):197-200.
[4] 郭广浩,刘志哲,孟庆龙,等.多级并行流水FIR数字滤波器的设计与验证[J].现代电子技术,2015,38(1):69-72.
[5] 李凯勇.基于FPGA高效FIR滤波器设计[J].青海大学学报,2017,35(6):56-60.
[6] 张娜,李春祎.多相并行FIR滤波器的FPGA高速实现方法[J].无线电通信技术,2017,43(4):86-90.
[7] 周龙,王红玲,崔新莹,等.基于FPGA及分布式算法滤波器[J].电子设计工程,2017,25(23):139-142.
[8] 曹振吉,何敏.基于FPGA和Matlab的FIR数字滤波器[J].现代电子技术,2015,38(19):98-101.
作者信息:
杜 勇
(四川工商学院 电子信息工程学院,四川 成都611745)

