0  引言

    近年来，由于大量电力电子设备广泛应用，以及非线性、冲击性负荷迅速的发展，使得电网电压、电流受到严重的噪声污染，因此造成了电力系统中的电能质量下降的问题^[1-2]。广泛应用到工业生产中的高度自动化、智能化的电子产品对电能质量的要求非常高，这些设备会因为低质量的供电水平而不能正常工作，导致它们控制的工业生产线在运行过程中出现异常，从而造成巨大的经济损失^[3-4]。由此可见对电能质量信号进行检测和分析是非常重要的，而采集到的信号时常夹杂着噪声，会影响检测和分析的准确性，因此对采集到的电能质量信号进行去噪是非常有必要的。而小波变换特别适合应用于各种信号的去噪^[5-6]，自然在电能质量信号去噪上它比其他方法更具有优势。文献[7]采用白噪声检验的方法得到最适合的小波分解尺度，提出了新的阈值函数，此函数连续且高阶可导，一定程度上避免了软、硬阈值函数各自的缺点，提高了去噪的性能。文献[8]首先介绍了几种国内外典型的改进阈值函数的算法，然后在传统阈值函数优缺点的基础上，得到了新的去噪方法，即双变量阈值函数去噪。局部放电仿真信号通过该方法去噪，其效果优于该文中提到的几种消噪方法。文献[9]基于软硬阈值方法的缺点，构造出新的阈值函数，然后采用仿真实验进行对比，得出该算法好于传统算法的结论，并且该函数更适合进行各种数学处理。

    本文基于小波软、硬阈值函数的缺点，对软阈值函数的进行处理，提出了新的小波阈值函数，通过实验仿真来分析验证。实验结果显示，相对于传统软阈值和硬阈值方法，电能质量信号通过本文改进的新的阈值算法进行去噪，去噪后计算出的信噪比都得到了提高，而且均方根误差却降低了。

1  小波变换

    若给定一个函数ψ(t)，令ψ(t)∈L²(R)（L²(R)指的是实数空间且平方可积，即能量有限的信号空间），其傅里叶变换是ψ(t)。当ψ(t)满足允许条件：

    公式（2）中a、b均为常数，且a>0，若a、b不断变化，就可以得到一系列子小波ψa,b(t)。

2  小波阈值去噪

    假定电能质量信号f(t)在传输过程受到了噪声s(t)的污染，则其实际含噪信号为：

2.1  阈值函数

    通常阈值函数可以分为两类：即硬阈值、软阈值函数。

    假设一个信号（或系数）的值小于给定的值，则显示为0，即

2.2  阈值门限

    常见的选取阈值门限的规则有四类：通用阈值规则（sqtwolog规则）、无偏风险阈值规则（rigrsure规则）、混合型阈值规则（heursure规则）和最大最小阈值规则（minimax规则）。 

    （1）通用阈值规则

    假定含噪信号X（t），在尺度1~m(1<m<K)上通过小波（包）变换分解尺度，小波系数的个数相加为n，K即二进尺度参数，令噪声的标准差为σ，那么通用阈值可以表示为：

    其中通用阈值的大小是固定不变的，也称之为固定阈值规则。

    （2）无偏风险阈值规则

    无偏风险阈值规则是通过史坦无偏似然估计原理自适应选择阈值。一个给定的阈值T，进行计算得出T的似然估计，然后对T进行最小化，就可以得到所谓的无偏风险阈值。

    （3）混合型阈值规则

    混合型阈值规则也称为启发式阈值选择。混合型阈值规则实际上是无偏风险阈值规则和通用阈值规则进行混合，也就是选取的是最优预测变量阈值。如果信噪比很小，选择无偏风险阈值规则会产生较大的偏差，此时就应该选择通用阈值规则。

    （4）最大最小阈值规则

    采用的阈值是固定不变的，通过该方法可以得到一个最小均方误差的极值。在统计学上这种极值原理是用来设计估计器的。那么可以假设被消除噪声噪的信号与未知回归函数的估计式是相近的，这样该极值估计器就可以达到最小化一给定函数集的最大均方误差的效果。

3  改进的小波阈值去噪

    小波阈值去噪最关键有两点：如何确定阈值函数和选取阈值门限。传统软、硬阈值去噪法在现实生活中得到了广泛的应用，也有比较好的效果，但还是存在缺点。由于硬阈值函数是不连续函数，数学意义上不容易处理，并且会产生一定的间断点，从而会使重构所得信号出现振荡的现象。软阈值函数是连续函数，在一定程度上克服了硬阈值的两个缺点，但该方法会减小绝对值大的小波系数，一定程度上造成了高频信息的损失，这样会导致信号的边缘模糊。而造成的高频信息损失是跟阈值门限的选取有直接关系的，所以为了增加阈值去噪的效果，选取合适的阈值门限非常关键。

    本文最主要改进了阈值门限，通过改进后的阈值门限与软阈值函数相结合来构造一种新的小波阈值去噪法。

    新阈值函数定义为：

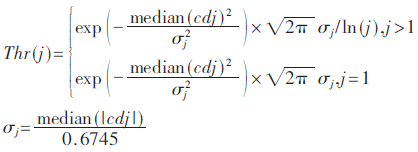
其中，σ_j即第j层噪声标准差的估计值，cdj即第j层的小波系数，Thr(j)即第j层的阈值门限值，median是对小波系数cdj的绝对值取中位值。

4  实验仿真

    本文以电压暂升信号为例进行仿真。电压暂升信号的数学表达式为：

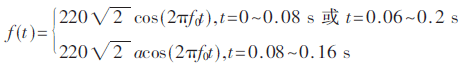
    其中a=1.8，f₀=50 Hz。

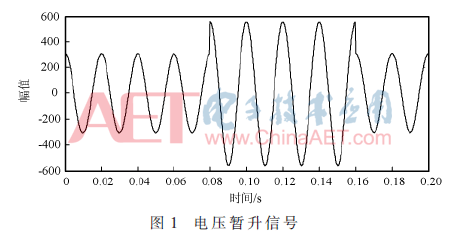
    图1是利用MATLAB模拟的电压暂升信号，由于考虑到噪声的影响，在电压暂升信号模型中叠加了噪声，其信噪比为15 dB。通过db8小波对加噪后的信号进行5尺度分解，再采用改进后的阈值函数对其进行去噪，然后与传统的软、硬阈值方法进行对比，如图2所示。

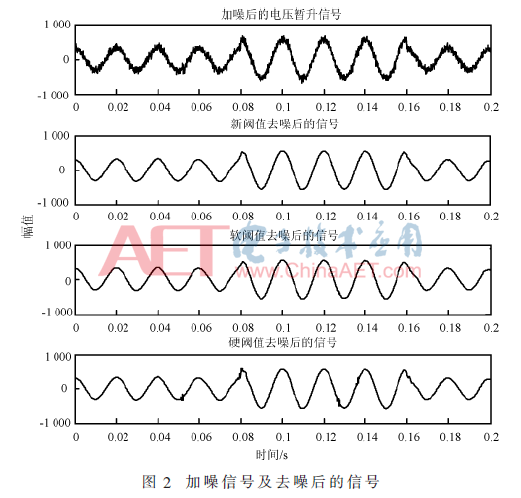
    从图2中可以看出，新阈值去噪后的信号和软阈值去噪后的信号相对比较光滑，硬阈值去噪后得到的信号还存在明显的毛刺，从肉眼上看新阈值去噪法和软阈值去噪法的去噪效果相对较好，但是平滑作用也会丢失部分原始信号中的有用信息，因此需要定量地研究这两种方法的去噪效果。定量判断去噪性能有两个指标：即去噪后的信噪比(SNR)和均方根误差(RMSE)，对同一含噪的信号, 去噪后的信噪比越大、均方误差越小，去噪效果越好。

    为了定量地研究算法效果的好差，现在各种相同输入信噪比的条件下，对比三种阈值算法的输出信噪比的大小，来验证算法的有效性。因为噪声是随机的，所以需要多运行几次取平均值，而图3是运行30次之后，求平均值得到的三种算法输入信噪比与输出信噪比的关系曲线。

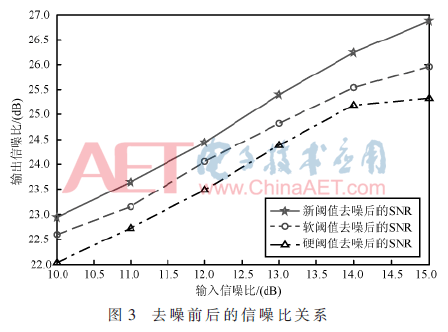
    从图3中可以看出本文提出的新阈值算法去噪后得到的信噪比在添加相同信噪比的噪声的情况下都是这三种方法中最高的，而这三种去噪方法有个相同点，即与输入信噪比是成正比的。虽然软阈值算法去噪后得到的信号波形也比较光滑，但是它去噪后的信噪比比新阈值法的要小，这是因为它的过度光滑影响了其去噪的性能。综上所述，采用新阈值去噪算法是这三种方法中去噪性能最好的，并且在添加不同信噪比的噪声的情况下，都能取得较好的去噪效果。

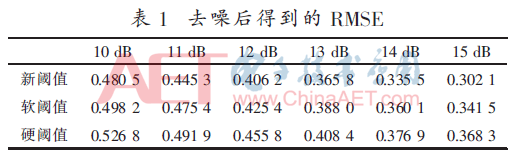
    表1是计算30次后求平均值得到的去噪后的均方根误差（RMSE），由表中可以看出新阈值法去噪后得到的均方根误差都是最小的，这也充分证明了新阈值的去噪性能优于传统的软、硬阈值去噪方法。

5  结束语

    本文针对传统软、硬阈值函数去噪法，改进了阈值门限，从而提出了新的小波阈值去噪方法。大量实验证明，新的阈值去噪算法去噪后的信噪比增益和均方根误差要优于传统软、硬阈值去噪法，因此能更好地去除电能质量信号中的噪声，较好地保留电能质量信号突变信息。并且实现方便, 去噪效果比较理想，又具有很好的灵活性和数学特性，因此有较大的工程实用价值。

参考文献

[1] 舒泓．电能质量扰动检测和分类问题的研究[D]．北京：北京交通大学，2008．

[2] 秦英林．电能质量扰动的自动识别和时刻定位研究[D]．济南：山东大学，2010．

[3] 肖湘宁．电能质量分析与控制[M]．北京：中国电力出版社，2004．

[4] MATH H J Bollen．Understanding power quality problems：voltage sags and interruptions[M]．New York：IEEE Press，2000． 

[5] Elise Mostacci，Caroline Truntzer，Hervé Cardot．Multivariate denoising methods combining wavelets and principal component analysis for mass spectrometry data[J]．PROTEOMICS，2010，10(14)：2564-2572．

[6] Florian Luisier，Cédric Vonesch，Thierry Blu．Fast interscale wavelet denoising of Poisson-corrupted images[J]．Signal Processing Magazine，2010，90(2)：415-427．

[7] 刘恒冰，韩世勤，刘晶．基于新阈值函数及最优尺度的小波去噪研究[J]．计算机工程与应用，2007，43(24)：72-74．

[8] 刘卫东，刘尚合，胡小锋．小波阈值去噪函数的改进方法分析[J]．高电压技术，2007，33(10)：59-63．

[9] 张维强，宋国乡．基于一种新的阈值函数的小波域信号去噪[J]．西安电子科技大学学报，2004，31(2) ：296-299．

作者信息:

谢妮娜，应国德，周  戈

（浙江台州供电公司，浙江 台州 318000）