在目标识别算法中，最为关键的是目标特征的提取。一般以提取物理特征为主，而其中寻找图像在缩放、平移和旋转情况下的不变特征一直是目标识别领域的研究方向之一。这些不变特征是良好区分不同目标物体的重要标志。迄今为止，图像识别" title="图像识别">图像识别算法己有多种，如不变矩法^[1]、相关法^[2]、判别熵最小化法、归一化转动惯量(NMI)法^[3]等。但以上几种目标识别方法较为复杂，对复杂图像识别效果也并不理想，在实时性要求较高的图像处理领域具有一定的限制。
　　脉冲耦合神经网络PCNN（Pulse Coupled Neural Networks)是上世纪90年代形成和发展的一种新型神经网络。PCNN有着生物学的背景，是依据猫、猴等动物大脑视觉皮层上的同步脉冲发放现象提出的^[4]，已被广泛应用于图像处理领域。在图像模式分类与识别中，常见的有PCNN与后续处理模式识别器的结合[5，6]或与其他方法相结合^[7]的方式；文献^[8]给出了基于PCNN分割二值图像熵序列的图像识别方法。本文基于PCNN提出了一种新的图像特征提取与识别方法，该方法能够对整幅图像的特征提取，且提取的识别参数少，准确率高。
1 PCNN模型基本原理
　　PCNN也称为第三代人工神经网络。PCNN的每个神经元一般由三部分组成：接收部分、调制部分和脉冲产生部分，用离散数学方程描述如下[9]：
　　
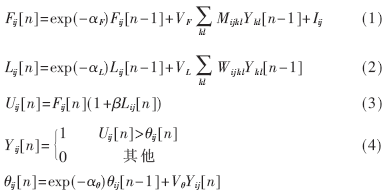
　　其中ij下标为神经元的标号，I_ij、F_ij、L_ij、U_ij和θ_ij分别为神经元的外部刺激(图像像素构成的矩阵中第N_ij个像素的灰度值）、反馈输入、连接输入、内部活动项和动态阈值，M和W为连接权矩阵(一般W=M)，VF、VL、Vθ分别为幅度常数，α_F、α_L与α_θ分别为时间衰减常数，n为迭代次数，Y_ij为二值输出。
　　在用PCNN进行图像处理时，将一个二维PCNN网络的M×N个神经元分别与二维输入图像的M×N个像素相对应。在第一次迭代时，神经元的内部活动项就等于外部刺激I_ij，若I_ij大于阈值，这时神经元输出为1，为自然激活，此时其阈值θ_ij将急剧增大，然后随时间指数衰减。在此之后的各次迭代中，被激活的神经元通过与之相邻神经元的连接作用激励邻接神经元，若邻接神经元的内部活动项大于阈值则被捕获激活。显然，如果邻接神经元与前一次迭代激活的神经元所对应的像素具有相似强度，则邻接神经元容易被捕获激活，反之不能被捕获激活。因此，利用某一神经元的自然激活会触发其周边相似神经元的集体激活，产生脉动输出序列Y[n]，且它们形成了一个神经元集群，从而可实现相关特征信息的提取与处理。
2 改进型PCNN赋时矩阵图像识别算法
2.1 改进型PCNN模型及其赋时矩阵
　　传统PCNN模型的关键思想是其非线性调制耦合机制和阈值指数衰变机制，而非线性调制耦合机制是核心。传统PCNN模型中虽然其阈值是指数衰降的，但又是反复变化的，即经过长时间(或短时间)的衰降之后必然会有一次由于神经元激活造成的突然上升，之后又衰降，然后又突然上升……显然，这种变化规律不符合人眼对亮度强度响应的非线性要求，而且这种阈值机制使得处理后的大量信息蕴含在神经元的激活周期(频率)或者激活相位中，而直接的二值输出图像却并不包含全部的信息。为克服上述缺点，本文对阈值函数做了改进，即把随时间反复衰变的指数函数改进成为随时间单调递减指数函数并对模型进行了简化，其表达式如下：
　　
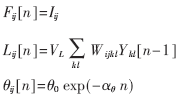
　　其中，U_ij[n]、Y_ij[n]的表达式与式(3)、式(4)相同。改进型PCNN用于图像处理时，有以下关键概念：(1)神经元的外部输入是与之相关联像素的灰度值，即F_ij[n]=I_ij；(2)所有神经元结构相等且各个神经元的参数一致；(3)每个神经元接受与之距离为R以内的神经元连接输入，内部连接矩阵W是一个3×3的方阵，每个元素的值为中心像素到周围每个像素的欧几里德距离的倒数(R^-1)；(4)每个像素所对应的神经元只能被激活一次。
　　当改进型PCNN对图像进行迭代处理时，在此定义一个赋时矩阵T，其大小与外部输入I、输出Y相等，并且T中的任一元素与I、Y联系的神经元一一对应，在T中存储与每个神经元点火时间相联系的时刻信息，即T_ij是第(i，j)个神经元的点火时间（或次数）。在本文中定义T_ij为第(i，j)个神经元第一次点火的时间：
　　
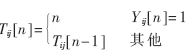
　　赋时矩阵反映了基于图像空间信息的时间域信息。它忠实地记录了与每个神经元点火时间相关的信息，分别有以下几种情况：(1)如果该神经元从未点过火，则在T中对应点的值为0；(2)在第n时刻第一次点火，在T中对应点的值为n；(3)该神经元已点过火，则T中对应点的值保持上一次的值不变。其迭代过程一直进行到所有神经元都点过火，T中的元素值均不为0，最后形成PCNN赋时矩阵T。
2.2 直方图矢量重心特征
2.2.1 基本概念定义
　　二维数字化灰度图像f(i，j)的M×N个像素可看作是XOY平面上的M×N个质点，像素的灰度值f(i，j)就是相应质点的质量。结合物理学相关概念[10]，对图像作如下定义：
　　定义1 二维灰度图像所有的灰度值之和定义为该灰度图像的质量，记为m，则：
　　
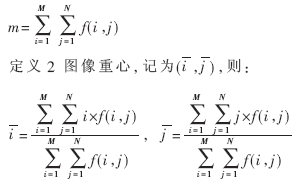
　　对于均匀灰度值的二维图像，图像的重心亦即该图像所占平面图形的形心。
2.2.2 直方图矢量重心
　　当对二维图像求其直方图H(g)时，H(g)是对于g的一维函数，其中g为图像的灰度，其值介于0～L（最大灰度值）。则H(g)是一个对于g的L+1维向量，对其利用上述定义，则有如下关系式：
　　
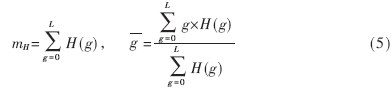
　　(5)式中分别定义为直方图矢量的质量和直方图矢量的重心。
　　由于原始图像的直方图不含有空间信息，所以不同的图像有可能具有相同的直方图。鉴于此，上述直方图矢量的重心和归一化直方图矢量重心质量不能反映图像的特征，不能用于图像的识别；但当对原始图像进行PCNN处理，形成PCNN赋时矩阵，将赋时矩阵作为一幅图像求其直方图及上述相关物理量时，PCNN在迭代过程中利用了调制耦合机制，形成赋时矩阵的直方图矢量既包含像素的灰度信息，又包含像素的空间信息；赋时矩阵直方图矢量的重心能忠实地反映图像特征,其表达式如下：
　　
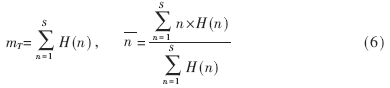
　　在(6)式中n为赋时矩阵T中对应神经元的激活时刻，S为最大迭代时间，H(n)为T的直方图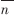，为T直方图矢量的重心。
3 实验结果与分析
　　本文利用Matlab6.5语言，选用了100幅不同的256×256灰度人物图像作为图像识别模式库，对图像分别进缩放、旋转及平移等操作，然后按图1所示过程处理，对图像进行识别。
　　为保证PCNN对处理图像的统一性及该方法的可适用性，对不同图像的处理要求在同一PCNN模型下进行。参数是β=0.1，V_L=0.05，θ₀=256，α_θ=0.1，Y、L、U及T初值设为零，内部连接矩阵W=M是一个3×3方阵，网络中每个神经元只与欧氏距离≤R(R=3)的相邻神经元链接。

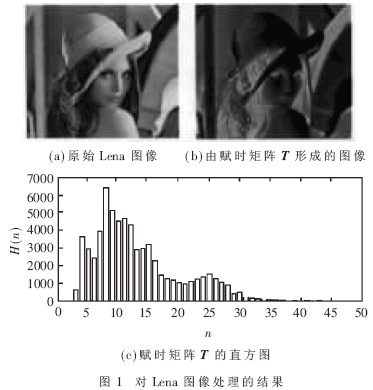
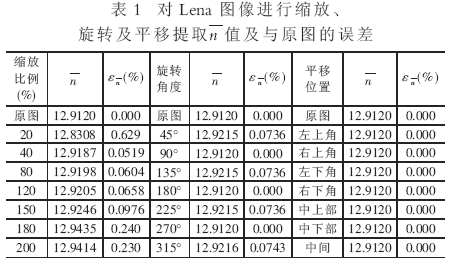
　　(1)对256×256 Lena图像进行旋转、缩放及平移处理操作实验。图1(a)是Lena原图，图1(b)是利用PCNN对Lena图像处理得到的T矩阵，图1(c)是T矩阵的直方图；图2(a)是Lena图像缩小为40%时T的直方图，图2(b)是对Lena图像旋转45°时T的直方图；其相关实验数据如表1所示。

　　(2)对图像模式库中部分不同图像特征提取后，与Lena图像识别对比。图3是模式库中待识别的部分人物图像，实验数据如表2所示。

　　
　　通过以上实验图表可以看出：(1)由于采用的阈值函数随时间单调递减，所以通过PCNN迭代形成的T矩阵图像是原图像的反白，如图1（b）所示；(2)当待识别目标图像与识别库中图像存在一定的比例变化、旋转及平移(见表1)时，采用PCNN直方图矢量重心特征识别，其识别误差小，具有良好的几何畸变(TRS)不变性；(3)若待识别目标图像与识别库中图像存在一定的差异，当采用本文方法进行识别时，虽有一定的识别误差，但误差不大。在实际图像识别过程中，当运用本文算法进行处理时，可预先设定直方图矢量重心识别误差判别值（例如本文可设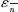=1.0%）来对待识别图像进行分类识别。