平均电流控制模式负载点电源（POL）的控制系统设计
2008-07-22
作者：虞叶芬1, 杜 丽1, 尚庆明
摘 要： 设计了一种基于MAX5060并采用平均电流控制" title="平均电流控制">平均电流控制模式的DC/DC变换器" title="变换器">变换器的控制系统。该变换器为输出电压" title="输出电压">输出电压可调的负载点电源（POL），采用大信号系统和小信号系统相结合的方法设计控制回路。详细分析了电源的控制系统设计。
关键词： POL 平均电流控制 同步整流BUCK
随着CPU等超大规模集成电路的发展，所要求的工作电压在日趋下降，而供电电流则日趋上升，并要求负载点电源（POL）具有更高的动态性能。
在当前的POL电源中，比较通用的主电路与控制策略是：主电路采用同步整流BUCK拓扑或多相交错BUCK电路；在控制策略方面，普遍采用电压型控制和峰值电流型控制。但是，由于电压控制模式不能控制各个电感的相电流，在多相BUCK中不能实现电流均衡的功能，而在单相BUCK中又需要额外的限流装置，并且对于输入电压的变化又响应较慢，由于这些原因，这种方案的缺点日益突出。峰值电流控制模式具有快速的负载动态响应，但对于噪声很敏感，并且占空比增加时，需要斜坡补偿。
平均电流控制模式具有较多的优点：在多相变换器中，具有自动电流均衡的能力；采用电感电流作为反馈信号，并且在电流环" title="电流环">电流环中引入一个高增益电流误差放大器，电流环的增益带宽可以通过设计这个电流误差放大器的补偿网络而达到最佳性能；与峰值电流控制模式的电流环频带相比，平均电流控制模式的电流环频带几乎与其相同，但低频增益却大很多；平均电感电流能够高度精确地跟踪电流编程信号；不需要斜坡补偿；抗噪声能力强。
本文主要介绍平均电流控制模式同步整流BUCK变换器的控制系统的设计方法，分别从大信号系统和小信号系统分析和设计控制回路，实验结果表明该控制方法切实可行。
1 平均电流控制BUCK变换器的大信号系统分析
当系统负载电流发生较大变化时（如从25%额定值变化到100%额定值），系统处在大信号扰动下工作，小信号的假设不再适用，小信号分析法得到的设计结果将与大信号扰动下的系统响应不一致，可能出现的情况是：用小信号法设计的开关转换系统在小信号下是稳定的，但在大信号扰动下系统可能不稳定，因此小信号分析结果不能预测大信号扰动下系统工作的实际特性。造成这一差别的主要原因是系统的非线性，包括功率电路的开关非线性和控制电路脉冲调制器的饱和非线性。
1.1 电流环增益限制条件一
在平均电流控制模式下，为了避免误差放大器进入饱和状态以及由于电流补偿网络输出的电压波形不与锯齿波相交或多次相交而导致的次谐波瞬态不稳定，必须要求PWM比较器的两个输入信号的斜率满足以下条件：被放大的电感电流的下降斜率不能超过锯齿波的上升斜率，否则，PWM比较器将不能正常工作。此标准即为“斜率匹配标准”。
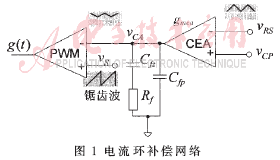
若采用图1所示的RC电流环补偿网络，则电流环补偿网络的Hc(s)为：
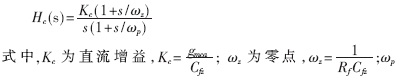为高频极点，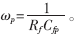
为满足斜率匹配标准，电流内环必须满足下式要求：
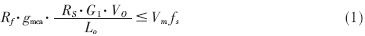
式中,Vm为锯齿波电压VS的峰值电压；RS是电流采样电阻；G1是电流采样信号的放大倍数；gmca是跨导型放大器的增益；VO和LO分别是BUCK变换器输出电压和输出滤波电感。即Rf需满足：
1.2 电流环增益限制条件二
在实际电路中，当变换器的输入电压升高或者占空比减小时，即使电流环增益已经满足了限制条件一的要求，变换器仍然可能出现开关不稳定，这与电流误差放大器（CEA）的输出信号VCA有关。
假设VCA的纹波峰峰值为图2所示的Vd，若Vd降到了电流误差放大器的最小输出限定值，则VCA的斜坡可能会被限幅或被箝位。若改变后的VCA斜率超过锯齿波斜率，就会导致开关不稳定。
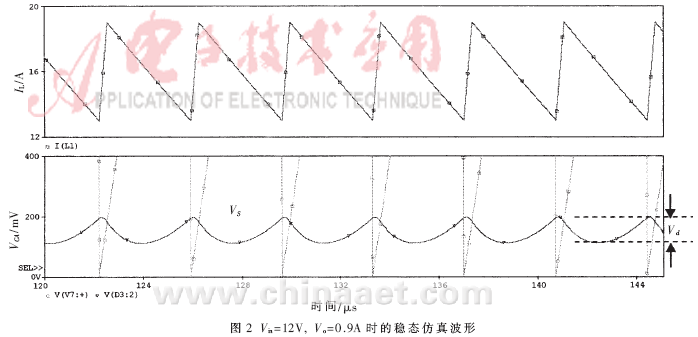
在实际电路中，应使VCA信号的纹波峰峰值Vd相对于其直流值要小，以避免电流误差放大器输出信号变形。当变换器输入电压Vg很大或者占空比D很小时，Vd值较大，这是因为Vd与被采用的电感电流纹波值ΔIL成比例。电感纹波值为：
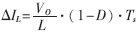
因此，还需要限制在开关频率处的电流环增益，使得峰峰值Vd满足：
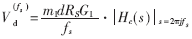
式中，m1为电感电流的上升斜率；Hc(s)为电流环补偿网络传递函数" title="传递函数">传递函数。
为避免电流误差放大器箝位，VCA应不超过VCA平均值的两倍(VCA平均值为d×Vm)。因此，要避免开关不稳定，开关频率处的电流环补偿网络增益应满足以下限制：
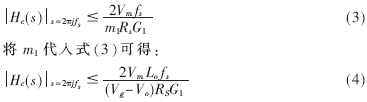
显然，对于高输入电压，根据式(4)计算的最大直流增益远小于根据式(2)的计算值。然而，在低输入电压时，式（4）的直流增益限制值将超过式（2）的计算值。因此，为了避免开关信号的不稳定，Rf应满足：
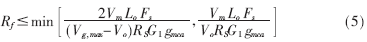
2 平均电流控制BUCK变换器的小信号分析
平均电流控制模式BUCK变换器的系统框图如图3所示（不考虑滤波电感和输出电容的串联等效电阻及死区时间的影响）。
电流环开环传递函数Ti(s)为：
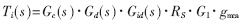
式中，G1为电流采样信号放大倍数；RS为电流采样电阻；gmca为跨导运算放大器增益；Gc(s)为电流环补偿网络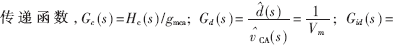
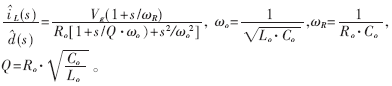
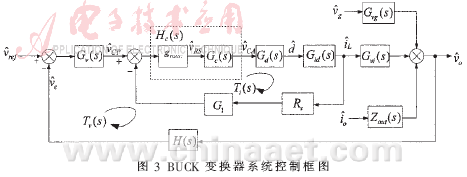
电压环开环传递函数Tv(s)为：
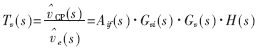
式中，Gv(s)为电压环补偿网络传递函数；Aif(s)为电流环闭环传递函数，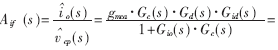
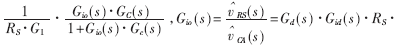
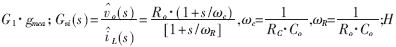
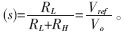
3 控制系统设计实例
结合上面关于平均电流控制模式的大信号系统与小信号系统的分析，设计了一个输入电压分别为12V和0.9V～3.3V/16A，输出电压为3.3V，最大电流为12A的POL电源。下面分别对电流环与电压环进行设计。
3.1 电流环设计
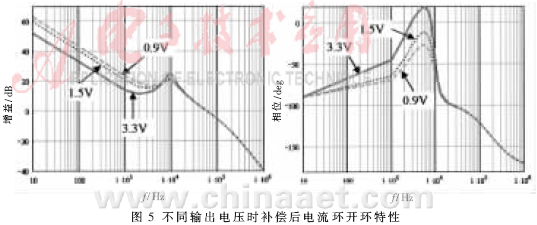
不同输出电压时，补偿前电流环开环特性如图4所示。当输出电压为3.3V时，幅频和相频特性在LC谐振频率（约11kHz）以上，系统以-20dB/dec斜率下降。
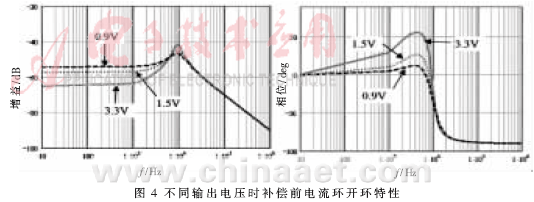
对于平均电流的电流内环，在小信号设计时的主要要求是：电流环补偿网络幅频特性在中频段具有平坦的特性；在交越频率处有足够的相位裕量。从以上两方面考虑，单极点-单零点补偿网络作为电流控制器是合理的。补偿网络如图1所示，CEA是一个跨导放大器，RC网络组成一个单极点、单零点补偿网络。在电流环补偿网络Hc(s)中，直流增益Kc按照上述讨论计算；零点ωz 用于扩展交越频率，一般应小于主电路LC谐振频率ωo，通常为其1/3或1/2；高频极点ωp主要用于滤除被测电感电流信号的开关纹波，以增强抗噪声能力，一般来说ωp应接近开关频率。
根据电流环最大增益限制条件一和限制条件二，利用式（5）可以得到Rf最大值。Rf应小于3kΩ，可以取Rf=2kΩ。
在多输出电压的POL电源中，当Vo=3.3V和Dmax=0.275时，电流环最大交越频率值最小，即：
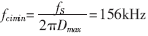
从上式可知，电流环的交越频率应小于156kHz。平均电流控制模式不仅与峰值电流控制模式一样具有很好的电流环带宽，而且由于其低频极点很低，低频增益很高，使电感电流的平均值能很好地跟随控制电压Vcp的变化。
补偿后的电流环开环特性如图5所示。在低频段，以-20dB/dec的斜率下降、直流增益趋于无穷大，因此符合理想条件，系统的稳态误差很小。在中频段，相位裕量大于60°。在高频段，在频率大于fp后，幅频特性的下降斜率为-40dB/dec，减少了主电路中开关信号高次谐波的影响，并能抑制由于寄生参数引起的衰减振荡信号。
3.2 电压环设计
电流环的闭环传递函数Aif(s)为电压环传递函数的一部分，补偿前电压环的开环传递函数为：
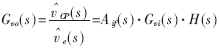
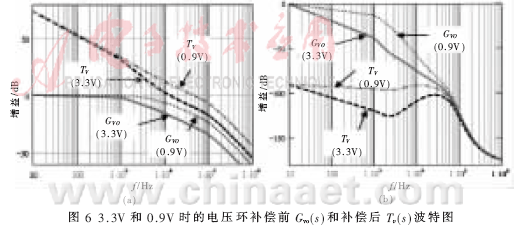
补偿前电压环的开环传递函数Gvo(s)如图6（a）所示。由幅频特性可知，补偿前电压环开环传递函数中，交越频率太低（<100Hz）。
补偿网络选择Ⅱ型网络，即低频为积分环节的单极点、单零点网络。由于电压误差放大器的带宽为3MHz，开环增益为70dB，约在300kHz处提供一个极点fp，因此，电压环补偿器选择单极点、单零点的RC网络，如图7所示。
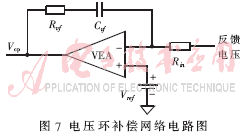
补偿网络的传递函数Gv(s)为：
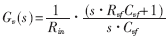
补偿后电压环开环传递函数Tv(s)为:
Tv(s)=Gv(s)·Gvo(s)
其波形图如图6（b）所示。
由于该POL有六种不同的输出规格，为了减小低输出电压时电压环的交越频率过高，以致于可能接近电流环的交越频率，需要将零点设置在输出阻抗较小时引起的极点处。因此，在约7kHz处设置一个零点，以使低输出电压时中频段增益降低。由于电压外环控制确定了系统对负载电流的响应，其截止频率fcv应小于电流内环的截止频率fci。
由图6可以看出，当输出电压为3.3V时，电压环的交越频率约为13kHz，相位裕量超过60°；当输出电压为0.9V时，电压环的交越频率约为47kHz，相位裕量也超过60°。因此，电源在多种电压等级时系统是稳定的。
所设计的POL样机，输出滤波电感为Lo=0.6H，选用Maxim公司的MAX5060控制器，样机规格符合DOSA标准，尺寸为50mm×14mm×7mm。
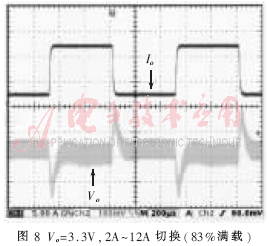
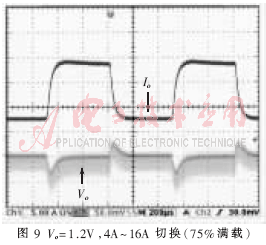
图8和图9是输出电压分别为3.3V、1.2V时的动态响应波形。从图中可以看出，V0=3.3V时，恢复时间仅为100μs，动态响应电压峰峰值为360mV。V0=1.2V时，恢复时间仅为100μs，动态响应电压峰峰值为100mV;其他输出电压时动态电压峰峰值也均在10% V0内。
本文讨论了平均电流控制模式负载点电源的控制系统设计。由于系统的非线性，包括功率电路开关非线性和控制电路中脉冲调制器的饱和非线性，平均电流控制模式的大信号系统需要满足两个限制条件，并保证各输出电压等级下小信号系统的稳定性。实验结果表明，该设计方法能实现变换器良好的动态响应性能。
参考文献
[1] COOKE P. Modeling average current mode control.Applied Power Electronics Conference and Exposition,2000:256-262.
[2] DIXON L. Average current model control of switching power supplies. Unitrode Application Note U-140, 1993.
[3] SUN J, BASS R M. Modeling and practical design issues for average current control. Proceedings of IEEE Annual Applied Power Electronics Conference and Exposition：APEC’99, 1999, 2:980-986.
[4] 蔡宣三，龚绍文. 高频功率电子学（直流-直流变换部分）. 北京：科学出版社，1993.