0 引言

    查找浮地交流系统对地绝缘故障最常用的方法是工频零序电流判据[1-3] ，但当出现三相绝缘同时降低或接地电阻较大时，该方法将难以判断。为此，低频信号注入法开始被用来解决该类问题，通过对直流电网的应用分析，发现该方法检测灵敏度随着电网对地电容的增大而降低 [3,4]，这一结论同样适用于交流电网。为了克服电网对地电容的影响，笔者尝试采用了稳态直流信号注入方法，通过霍尔传感器对负载支路漏电流的感应和直流成分的提取来判断绝缘故障支路，理论上是优越的，但在工程实现上较难。通过工业现场的应用，发现霍尔传感器受空间杂散磁场的干扰大，尤其是在穿心口径大且漏电流微弱的情况下；当霍尔传感器数量多且较分散时，其工作电源的提供在工程上复杂且电源品质难以保证；霍尔传感器间的偏差校正较复杂，这些问题影响了稳态直流信号注入方法在工程上的应用。基于此，本文提出了一种能有效克服电网分布电容等参数和工频变量影响，且工程上易实现的方案—阶跃响应法，其基本思想是向电网注入一直流阶跃信号，利用负载支路暂态漏电流响应中阻性电流与容性电流在时域上分离，而与电网工频信号在频域上分离的特性，通过高精度传感器对暂态漏电流的感应，并采用数字滤波手段，将反映支路对地绝缘电阻大小的阻性电流提取出，从而判断出绝缘故障支路。

1 阶跃响应法原理
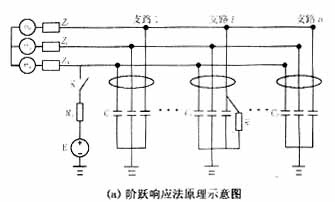
    阶跃响应法应用于浮地交流系统绝缘故障支路定位的原理如图1(a)所示，三相电网母线给n条负载支路供电，每条支路对地电容分别为C1,C2,...Cn，交流漏流传感器环套在每条支路三相电缆上，当电网出现低绝缘故障时，假设第i条负载支路绝缘下降，且绝缘电阻为RJ，闭合开关K，即向电网投入了直流阶跃信号，直流电势为E，限流内阻为R0。
1.1 故障支路对阶跃信号的电流响应
    阶跃注入电网时，负载支路暂态漏电流同时包含有阶跃响应成分和工频成分。为便于讨论，首先以故障支路i为例，分析直流阶跃信号单独作用时的暂态电流响应。由于交流电源内阻抗z远小于限流内阻和绝缘电阻，则图1(a)所示电路可等效成如图1(b)所示简化电路。

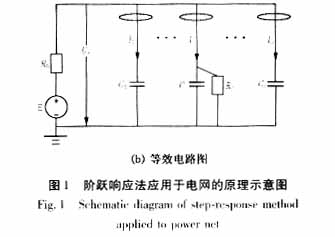
    向电网注入直流阶跃信号时，故障支路的漏电流(传感器的穿心电流)为

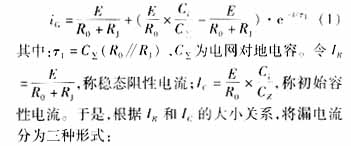
    ① 当IR = IC时，或电网对地无电容时，漏电流为阶跃形式，阶跃幅值为IR，见图2曲线b；
    ② 当IR > IC时，漏电流阶跃上升至IC后，按指数规律上升至IR，见图2曲线c；
    ③ 当IR < IC时，漏电流阶跃上升至IC后，按指数规律下降至IR，见图2曲线a；

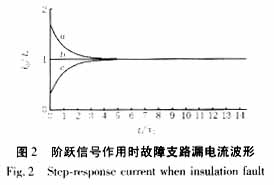
    由图2可知，阶跃信号作用于电网时，流过绝缘故障支路的漏电流同时包含了反映接地电阻和对地电容信息量，而反映电容大小的电流量会按指数规律迅速衰减，并收敛于仅反映电阻大小的电流量上。因此，若能采用高导磁率材料制成的高精度交流电流传感器，使之能较准确地反映出故障电流的初始动态过程，则不难得到故障电流的波形，尤其是反映电阻大小的电流值，从而计算出故障支路接地电阻的大小。
1.2 穿心电流传感器的模型及其感应电流的计算
    电流传感器电气线路和磁路示意图见图3。原边电流为i1，副边电流为i2，副边匝数为w2，Φ为互磁通，Φ2s为副漏磁通，副边接负载电阻R，电流、电势和磁通的正方向如图示。

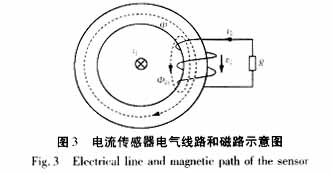
    由于对穿心式电流传感器，原边电流可认为不受副边电流的影响，因而以下，仅对副边回路进行分析，副边的电压方程可表达为：

式中，Φ2表示键链副绕组的总磁通，亦即Φ2=Φ+Φ2s。其中Φ=12(i1+w2i2),Φ2s=2sw2i2,12和2s分别表示互磁路和副漏磁路的磁导[6]。则(2)式可表达为：

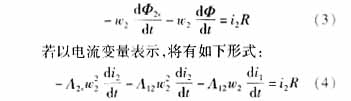
     称副绕组漏感，M=12w2，称原副绕组间的互感。则式(4)可改写为:  

    如令L2=S2+Mw2表示副绕组的总自感，则式(5)又可改写为：

    对式(6)所表达的线形方程，可采用拉氏变换求解。因i1(0_)=0,i2(0_)=0,则(6)式经拉氏变换可表达为：

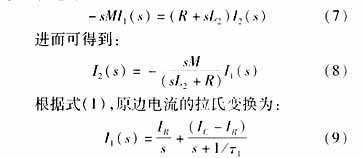
    式(9)代入式(8)后，可得：


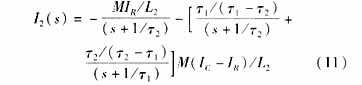
    由于传感器在设计时，L2很大，使得τ2>>τ1,于是(11)经拉氏反变换后，可得传感器感应电流i2(t)的近似时域表达式:

     为分析i2 ，同原边电流一样，分三种情况进行讨论：
    ① 当IR = IC时，副边感应电流阶跃上升至IR/w2后，按指数规律(时间常数为τ2)衰减至零，见图4曲线b；
    ② 当IR > IC时，副边感应电流阶跃上升至IC/w2后，先按指数规律(时间常数为τ1)上升，而后按指数规律(时间常数为τ2)衰减至零，见图4曲线c；
    ③ 当IR < IC时，副边感应电流阶跃上升至IC/w2后，先按指数规律(时间常数为τ1)迅速下降，而后按指数规律(时间常数为τ2)衰减至零，见图4曲线a。

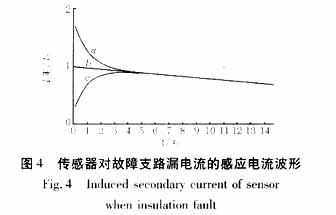
    从图4中，可以发现：
    ① 副边感应电流波形变化包含了两个指数变化规律，分别对应于时间常数τ1和τ2，且τ2>>τ1；
    ② 在波形初期，容性电流变化部分能较充分地反映在副边感应电流中，体现了传感器的互感应过程，且容性电流在很短的时间内迅速衰减并收敛至阻性电流上，时间常数为τ1； 
    ③ 初期过后，原边穿心电流稳定不变，阻性电流以较慢的速度衰减，时间常数为τ2，体现了副边大电感对电流(线圈磁通)变化的抑制过程。
    基于上述分析，交流电流传感器为满足阶跃响应法的要求，应能较好地感应原边电流微小的动态变化，且当原边电流稳定不变时，副边线圈中剩余磁链(电流)能以较大的时间常数缓慢衰减。为此，应采用极高导磁率的铁心材料及合理的结构形式，使其具有较大的互磁路的磁导12(互感M)和尽可能小的副漏磁路的磁导2s(副边漏感S2)，同时通过副边绕组匝数的增加，保证传感器的变比尽量趋近于原副边匝数之比，以满足传感器对微小动态变化的感应；自感L大，以满足剩余磁链(电流)以较慢的速度衰减的要求。
1.3 考虑到工频零序电流作用时的传感器副边感应电流
    当故障漏电流(传感器原边电流)同时有直流和工频交流信号时，对传感器副边感应电流的计算可采用叠加原理。对工频漏电流信号在传感器副边感应电流的计算，可采用副边参数变量归算至原边的方法。假定原副边漏感系数远远小于互感系数，可得到原副边电流的近似对应关系：

    其中，I0和α0分别为工频零序电流的幅值和起始相位角，f为工频电流频率。利用叠加原理可以得到有工频零序电流作用时的传感器副边感应电流：

    以IR > IC情况为例，可以得到如图5所示的传感器感应电流。

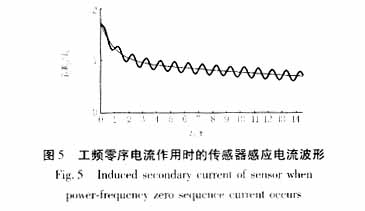
    由图可见，考虑到工频零序电流作用时的传感器副边感应电流在图5所示的波形基础上叠加了一工频交流信号。图中细线为无工频信号作用时的感应电流，粗线为考虑工频信号作用时的感应电流。
1.4 阻性电流的提取
    由上述分析可知，接地故障电阻大小反映在阻性电流中，而阻性电流由于具有在时域上与容性电流分离，在频域上又与工频零序电流分离的特点，因而为其提取提供了方便。其方法为：在阶跃信号注入时间3τ1-4τ1后(假定τ1已知)，容性电流已基本衰减完毕，由于τ2>>τ1，阻性电流几乎未衰减，感应电流仅包含阻性电流和工频零序电流，而后对其进行软件滤波，滤除工频成分，由于τ2>>1/f，则可以得到阻性电流衰减初期的值。

2 试验研究
2.1 试验条件
    试验电路如图1，电路参数设定为：E=110V，R0=2kΩ，RJ=30 kΩ， C∑=10μF。设计了环形穿心式电流传感器及其微弱感应信号的精密放大电路，实现对漏电流的检测。传感器铁心以磁导率极高的铁磁材料环形绕制而成，通过其有效截面尺寸和原副边匝数比等参数的有效设计，使传感器具有准确感应微小变化电流的能力，且在1mA∽100mA范围内变比有着良好的一致性，副边电感大，配以适当的负载电阻，可以使时间常数大于1s。
2.2 传感器原副边电流波形对照
    暂且不考虑交流工频量的影响，即假定交流电源电势为零。通过改变对地电容，分别得到了在IR < IC 、IR = IC 和IR > IC条件下，当阶跃信号作用时，故障支路的漏电流及其穿心电流传感器的感应电流的波形，如图6所示。图中上半部分和下半部分分别为传感器的原边漏电流和副边感应电流。

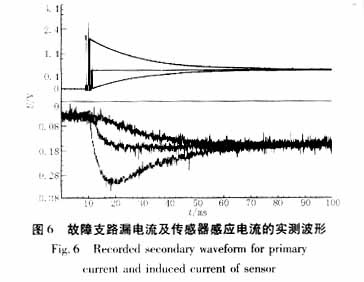
    实测波形中反映出的电流变化规律与前面的理论分析结果基本一致。值得注意的是，实测中感应电流并未随传感器原边的阶跃变化而发生阶跃跳变，这是由于副边漏感系数作用的结果。

3 结论
    (1) 阶跃响应法使暂态漏电流信号中反映接地电阻的阻性电流与反映对地电容的容性电流在时域上呈现分离性，而与电网工频漏电流在频域呈现分离性，易于提取，从而有效地克服了电网对地电容等系统参数和工频电流等系统变量对绝缘故障支路定位的影响。
    (2) 通过对传感器的合理设计，使之既能有效地响应原边电流的动态变化，又能使阻性响应电流缓慢地衰减，避免了稳态直流注入法必须依赖霍尔元件所带来的附加电源及电磁兼容性差的问题，从而保证了阶跃响应法在工程中实现的可能性。
    (3) 通过试验研究，发现实测结果与理论分析基本吻合，进一步验证了阶跃响应法的有效性。